
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Earth Sci. , 04 August 2020
Sec. Environmental Informatics and Remote Sensing
Volume 8 - 2020 | https://doi.org/10.3389/feart.2020.00331
This article is part of the Research Topic Frontiers in Seafloor Geodesy View all 21 articles
The Global Navigation Satellite System-Acoustic ranging combination technique (GNSS-A) is a recently developed technology to precisely detect seafloor crustal deformation. This method can also estimate km-scale underwater sound speed structure (SSS) as a by-product of monitoring seafloor crustal deformation. This paper evaluates the validity of the spatial gradient and its temporal variation of the SSS estimated by GNSS-A observations off the Kii channel before and after Kuroshio meandering. According to the comparison of the JCOPE2M reanalysis data and the in situ observation data, the GNSS-A estimated SSS has local structures that are not reproduced in this reanalysis but were detected by in situ data. In addition, we investigate the effect of observation time on the stability of SSS estimation. The results suggest that the sufficient time required for stable estimation depends on the spatial coverage of observation data, which depends on the depth of the site. As a result, the time resolution was derived to be about one hour at a site whose depth is 1500 m.
The Global Navigation Satellite System-Acoustic ranging combination technique (GNSS-A) was proposed and developed to extend the geodetic network to the seafloor by combining GNSS positioning with acoustic ranging technology (Spiess, 1985; Asada and Yabuki, 2001; Fujita et al., 2006). This observation technique makes it possible to accurately measure the seafloor movement and to detect various subseafloor geophysical phenomena due to co-, post-, and inter-seismic phases following a huge earthquake cycle (e.g., Sato et al., 2011; Watanabe et al., 2014; Yokota et al., 2016). Recently, Yokota and Ishikawa (2020) reported detection of tiny transient signals due to slow slip events. To monitor this kind of transient signals continuously, it is indispensable to upgrade the GNSS-A accuracy, which requires a better understanding of the underwater sound speed structure (SSS).
The uncertainty of the SSS is a major error source of GNSS-A observation. Our group has been developing analysis methods to estimate the SSS from GNSS-A observation (Fujita et al., 2006; Yokota et al., 2019). For example, Yokota and Ishikawa (2019) confirmed that the GNSS-A estimated SSS off the Bungo channel is almost consistent with the temperature gradient structure caused by the Kuroshio.
Detailed SSS was discussed using, e.g., seismic survey (Ruddick et al., 2009; Papenberg et al., 2010). Seismic oceanography was also conducted in the Kuroshio region (Tsuji et al., 2005; Nakamura et al., 2006). However, it is not possible to obtain this kind of data at various points at low cost and with high frequency. While seismic oceanography is suitable for understanding the details of complexity and ocean physical characteristics of fine scale ocean, GNSS-A oceanography might be useful for understanding location characteristics and long-term characteristics (seasonal changes and relationships with seafloor topographies). Understanding SSS effect in each technique may also lead to upgrading the accuracy of each technique.
This paper conducts surveys on the spatial gradient of SSS that affects the GNSS-A, by comparison between its analysis results and the ocean structure off the Kii channel before and after Kuroshio meandering. The estimated parameters are compared with ocean reanalysis data and in situ expendable bathythermographs (XBTs) and expendable conductivity temperature depth (XCTD) profilers data. The results depend on whether the Kuroshio is meandering or not. Especially in the case when the Kuroshio meandered, GNSS-A estimated SSS has a gradient that was not reproduced in the reanalysis used for the comparison. Additionally, we examine the temporal variation of the gradient parameters.
In the GNSS-A, to measure the movement of the seafloor accurately, the absolute position of a relay point located on the sea surface is determined by the GNSS, and the relative position between the relay point and the seafloor station is determined by acoustic ranging. As a result, the absolute seafloor position can be determined. The observation system is shown in Figure 1A. Please see Yokota et al. (2018) for details.
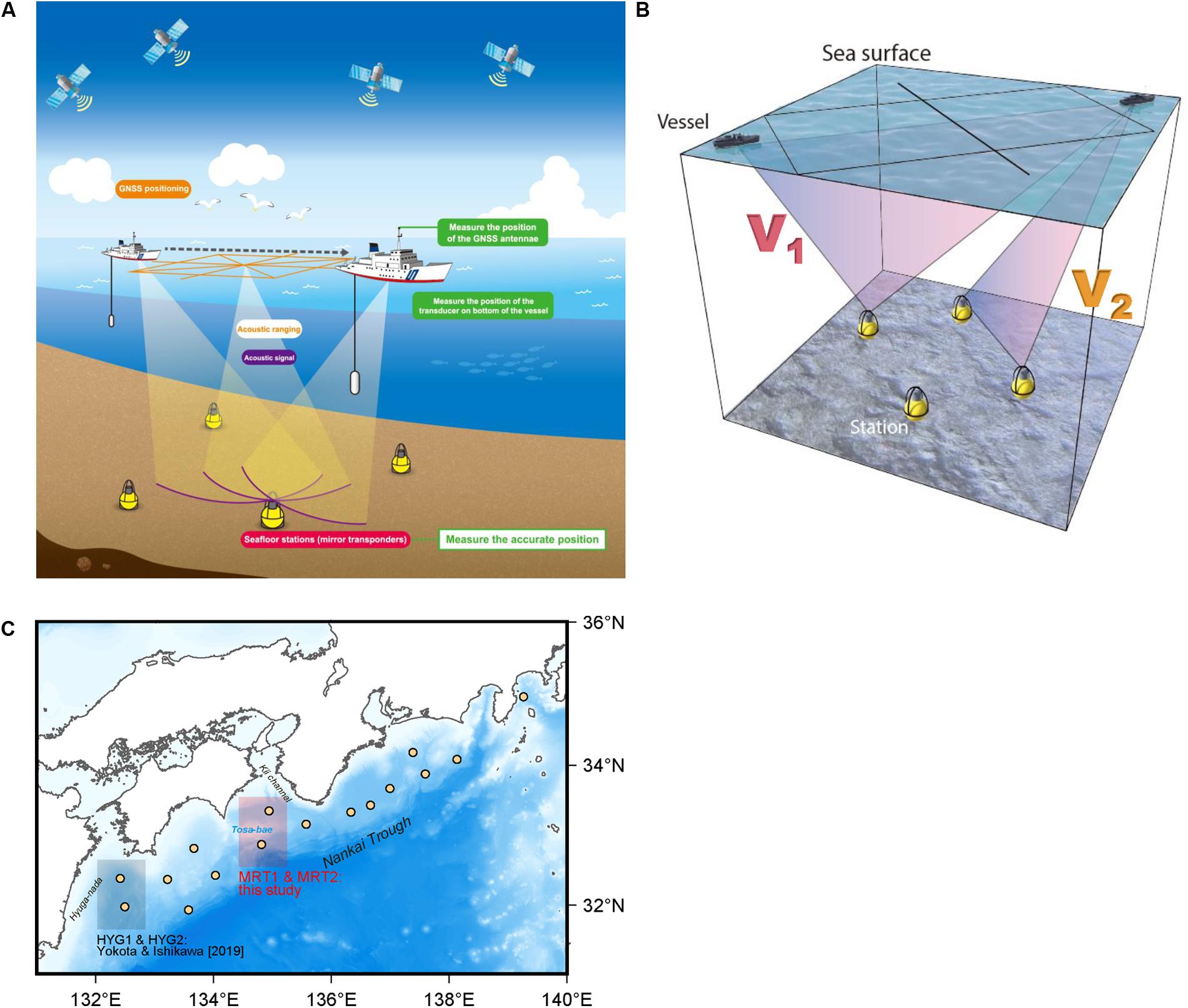
Figure 1. (A) A schematic image of the GNSS-A system. (B) A schematic image of scanning SSS. These figures are modified after Yokota et al. (2018, 2019). (C) GNSS-A sites (orange circles) along the Nankai Trough as of November 2018.
In the present day, the horizontal positioning accuracy of the GNSS-A is about 2 cm (1σ). Because the spatiotemporal variations of the SSS are more complex and larger than those of the ionosphere/troposphere which affect the GNSS positioning, the uncertainty of SSS is the largest error source of GNSS-A. Data obtained from in situ observations such as XBT/XCTD measurements can constrain the SSS, but cannot cover all of these variations in detail. Therefore, developing an analysis method for estimating the SSS in detail is an important research target for GNSS-A observation.
After the early work of Fujita et al. (2006) which estimates the temporal variation of the SSS by quadratic polynomial approximation, various techniques to process underwater SSS have been studied. Yokota et al. (2019) reinterpreted Fujita’s method and developed a technique that determines the shallow horizontal gradient of the SSS by performing pseudo-tomographic analysis within the triangle V1 (Figure 1B) connecting the moving ship and the seafloor station. Additionally, estimation of the SSS when fluctuations occur in deeper regions has been improved by using another triangle V2 (Figure 1B). Their detailed methodologies are described in Yokota (2019), Yokota and Ishikawa (2019), and Yokota et al. (2019).
Here, only the SSS estimation procedure (Figure 2 in Yokota et al., 2019) is described. First, we generate a horizontal layered SSS from XBT/XCTD observations as an initial parameter. After that, in the inversion analysis, an effect for each acoustic shot due to temporal and spatial changes is corrected. Here, the removal operations of the long-period component and the short-period V1 and V2 are performed step by step, and the routine is repeatedly performed until convergence. The parameters obtained here include high-rate GNSS errors as well as complex disturbances in the ocean. At present, it is difficult to properly evaluate this amount of error, and the evaluation method is a future research topic.
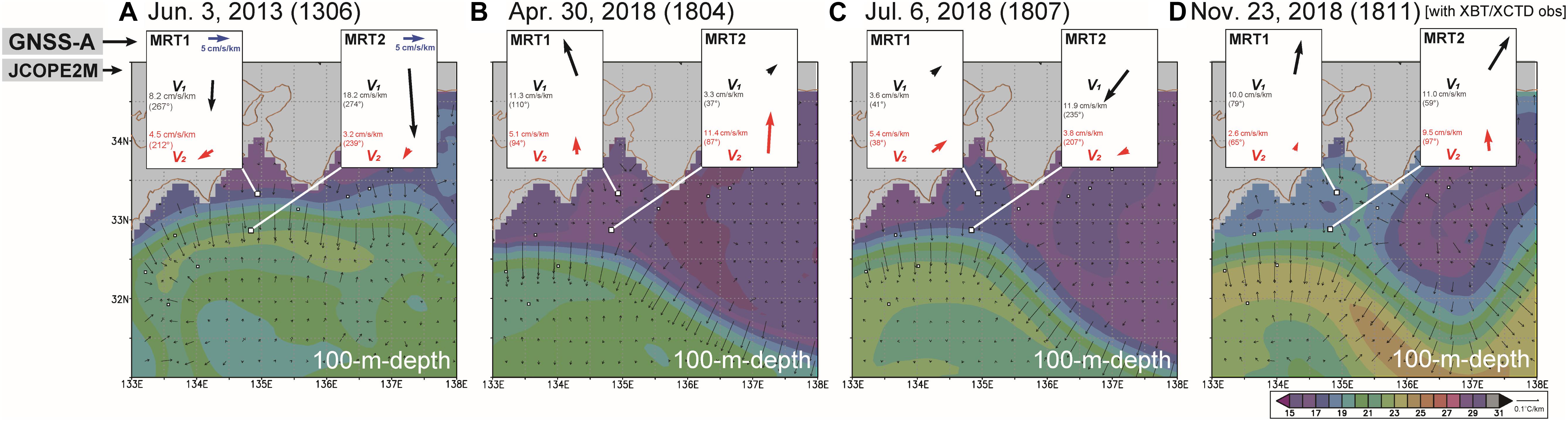
Figure 2. Gradient parameters extracted in GNSS-A [black (V1) and red (V2) vectors] and 100 m-depth temperature fields of the JCOPE2M reanalysis on observation dates, (A) June 3, 2013, (B) April 30, 2018, (C) July 6, 2018, and (D) November 23, 2018 for MRT1 and MRT2. The value of each vector (absolute value and counterclockwise angle from east) is written beside the vector. Scales of the water temperature and the temperature gradient vector of the JCOPE2M reanalysis are shown on the bottom right.
As discussed in Yokota (2019), the tendency of SSS depends on V1/V2. When V1/V2 is higher than the survey line range for the diameter of the array, which is about 2 in this study, the effect of shallower gradient becomes stronger, and when V1/V2 is lower than 2, the effect of deeper gradient becomes stronger. The depth tendencies of SSS cannot be determined quantitatively.
Generally, to understand the ocean structure, satellite observations are used to capture the global ocean surface property and in situ observations, such as XBT/XCTD, Argo float, are used to capture the vertical profile at a local point. In the GNSS-A, the overview of the horizontal gradient of the SSS is obtained. Because the spatial range of the obtained gradient depends on the size of the transponder deployment region, which is typically in the range of 2–6 km, the GNSS-A estimated SSS can have a slightly different perspective than those of other ocean observations. The GNSS-A may reveal structures that cannot be detected by other observations. Although there is no other way to precisely measure SSS in km-scale than costly XBT/XCTD dense observations, we examine the appropriateness of the GNSS-A estimation results by comparing with other data having different spatial scales such as in situ and reanalysis data.
Here, we use the data obtained at two sites off the Kii channel, namely, MRT1 and MRT2 (Figure 1C) in June 2013 (1306), April 2018 (1804), July 2018 (1807), and November 2018 (1811). The gradient parameters estimated from GNSS-A data for each observation campaign are represented as vectors V1 and V2 as shown in Figure 2. Although the vectors can be obtained for each acoustic shot data continuously, in section “RESULTS,” we discuss using the time average value from all acoustic shot data. Temporal variation of gradient vectors will be discussed in section “DISCUSSION.”
Supplementary Figure S1 shows residuals of travel time before and after corrections of V1 and V2 (colored cross for each station) (A and B), average sound speeds estimated before (gray line) and after corrections of V1 and V2 (colored line for each station) (C), and the position of the vessel relative to the center of the station array (D) for each shot in the final solution. For example, in the case of MRT2-1804 (Supplementary Figure S1bC), estimated average sound speeds for station-N (north) are always faster than station-S (south). As a result, a large northward V2 was obtained, suggesting the effect of deeper northward gradient. In the cases of 1811 (Supplementary Figure S1dC), although estimation results at both stations show temporal changes, it can be inferred from the small average V2 that the effects of the shallower gradients were larger.
Each vector in Figure 2 is pointing in the direction of higher sound speed. In 1306 and 1811, V1 is sufficiently larger than V2. This suggests that the SSS has a gradient only in the relatively shallow layers. However, the thickness of the gradient layer cannot be uniquely estimated. In contrast, the result obtained at site MRT2 in 1804 shows that V2 is larger than V1. This suggests that a gradient has emerged in a relatively deeper region. Small vectors at site MRT1 in 1807 suggest a weak gradient SSS.
JCOPE2M is a new ocean reanalysis data that is an advanced version of JCOPE2 used in our previous studies (Yokota and Ishikawa, 2019; Yokota et al., 2019). JCOPE2M is a data targeting the northwestern Pacific Ocean, produced by assimilating satellite and in situ observation data to an ocean model using a multi-scale three-dimensional variational scheme (Miyazawa et al., 2017, 2019). The model is based on the Princeton Ocean Model, with a horizontal resolution of 1/12 degrees. The model can express 10–100 km scale oceanographic phenomena, but detailed structure on the km-scale has not been completely represented. Here, we compare the GNSS-A estimated gradient vector of SSS with the JCOPE2M reanalysis.
Figure 2 shows the temperature and its gradient at 100 m depth, derived from the reanalysis during each observation campaign. In 1306, the northern edge of the Kuroshio lies around the vicinity of MRT1 and MRT2. The large southward gradient field V1 is consistent with the reanalysis (Figure 2A). This result is similar as ones off the Bungo channel (Yokota and Ishikawa, 2019), when the Kuroshio flows near the GNSS-A site.
After August 2017, when the Kuroshio began to meander, the southward gradient vectors around the two sites in the JCOPE2M reanalysis changed because warm seawater advected to the south (Figures 2B–D). In 1807 (Figure 2C), site MRT1 was located far from Kuroshio, and site MRT2 was located at the edge region of Kuroshio. Small extracted vectors at site MRT1 and southward vectors at site MRT2 are consistent with the reanalysis.
In 1804 (Figure 2B), the reanalysis indicates very weak gradients around the sites, because the Kuroshio was far away from the sites. In contrast, GNSS-A estimates a northward gradient vector which is inconsistent with reanalysis. In 1811 (Figure 2D), northward vectors at MRT2 were also inconsistent with a slight southward gradient in the reanalysis.
To fill the gap between the GNSS-A estimation and the reanalysis, in situ observation was carried out along a line crossing the Kuroshio in 1811. XBT/XCTD were dropped sequentially at evenly spaced points as shown in Figure 3A. Figure 3B shows the cross section of the underwater SSS, generated from the XBT and XCTD data. A shallow seafloor hill topography called the Tosa-bae bump is located between MRT1 and MRT2. It is possible that this structure affects the fine scale ocean structure in this region. The area of this topography is masked in Figure 3B.
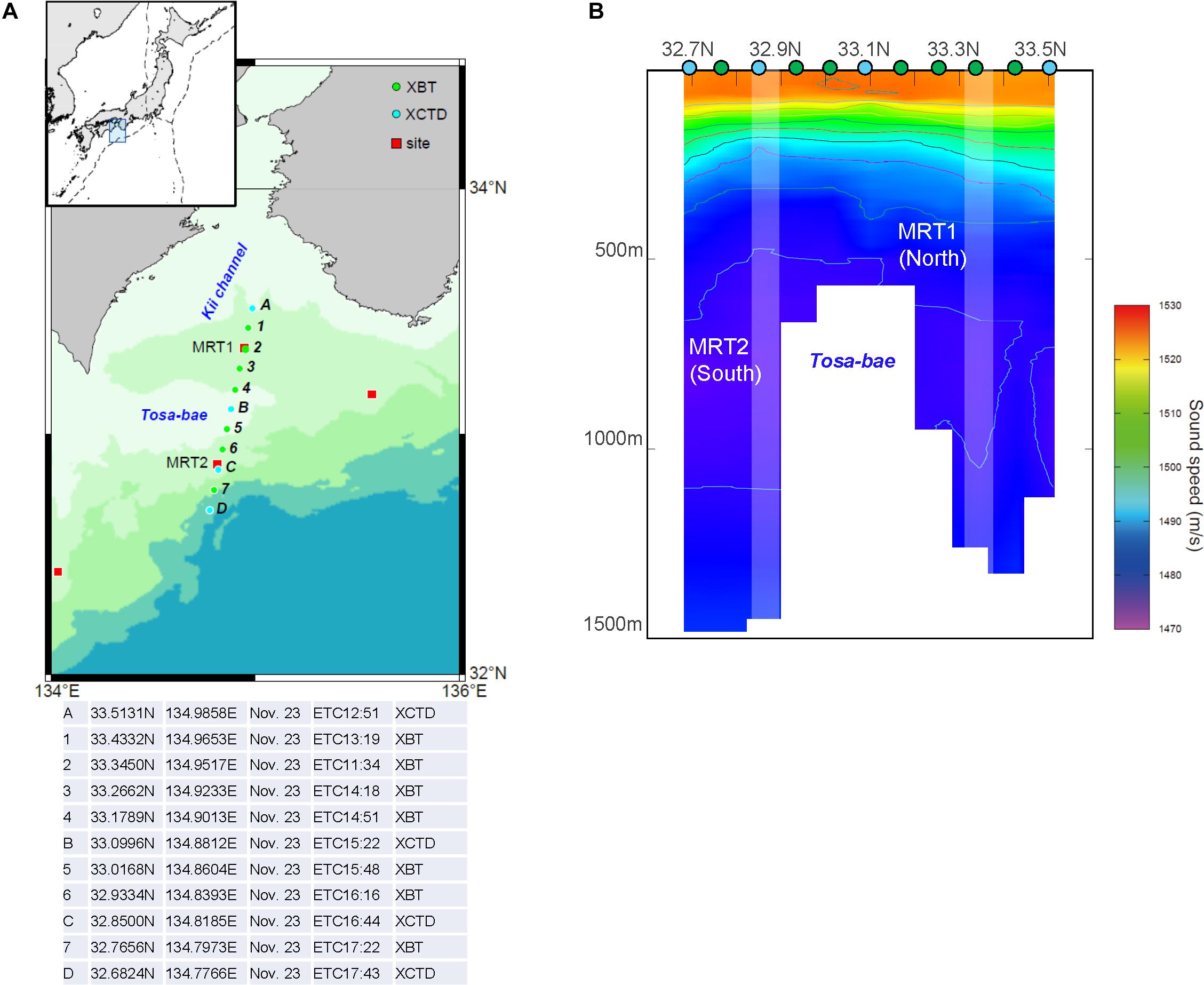
Figure 3. (A) Locations of the seafloor sites and direct sound speed observation points in November 2018. Red squares indicate seafloor sites MRT1 and MRT2. Green and light-blue circles indicate XBT and XCTD observation points, respectively. Details of XBT and XCTD casts are listed in the bottom table. (B) Resultant SSS cross section of direct observations. White bars indicate regions around sites MRT1 and MRT2. Green and blue circles at the surface indicate positions of the XBT and XCTD casts, respectively.
This result shows that there is a northward gradient around 33.2–33.5N and a southward gradient around 32.7–32.8N which are consistent with the reanalysis. The northward GNSS-A result at site MRT1 is thought to reflect the 33.2–33.5N gradient. In addition, different from the comparison at the Hyuga-nada sites in Yokota and Ishikawa (2019), there is partially complicated structure that does not appear in the reanalysis around 32.8–32.9N (200–300 m depth).
The northward GNSS-A result at site MRT2, which is inconsistent with the reanalysis, may reflect the km-scale structure around 32.8–32.9N shown in this in situ observation. The qualitative depth of a gradient structure can be inferred from the discussions in Yokota (2019) and Yokota and Ishikawa (2019). In the case of this GNSS-A estimation result (V1/V2 ≥ 2), we can indicate a possibility that there was a shallower side simple structure as shown in the in situ observation, though the quantitative depth cannot be determined. The comparison results suggest that GNSS-A was also affected not only by 100 km scale SSS as estimated by reanalysis but also by km-scale SSS as detected by detailed direct observation.
However, without costly dense (spatial and temporal) in situ observation, it is difficult to verify the GNSS-A extraction results in such a complicated case. To apply the GNSS-A estimated SSS oceanographically and to enhance the GNSS-A observation accuracy, more oceanographic in situ observations and validations will be necessary.
The km-scale structure may reflect the complexity of the underwater structure, such as internal gravity waves. In the vicinity of our study area, the Tosa-bae bump may have triggered such a complicated SSS. Matsui et al. (2019) showed that internal gravity waves driven by such topographic peaks affect GNSS-A positioning accuracy, using numerical simulation.
Up to the above section, we discussed using gradient values that have been time averaged over the entire observation time in each observation campaign. In principle, the gradient vector is estimated for each acoustic shot, which makes it possible to detect the time variation of the gradient vector. Yokota and Ishikawa (2019) and Yokota et al. (2019) visualized the time variation of the gradient vectors using one round of the survey line as shown in Figure 4A. However, the estimation of the gradient vector is stable only when the survey lines cover the whole observation area. Figures 4B–D show the effect of data coverage on the estimation of gradient vector in the cases using half, one third, and a quarter of all survey lines.
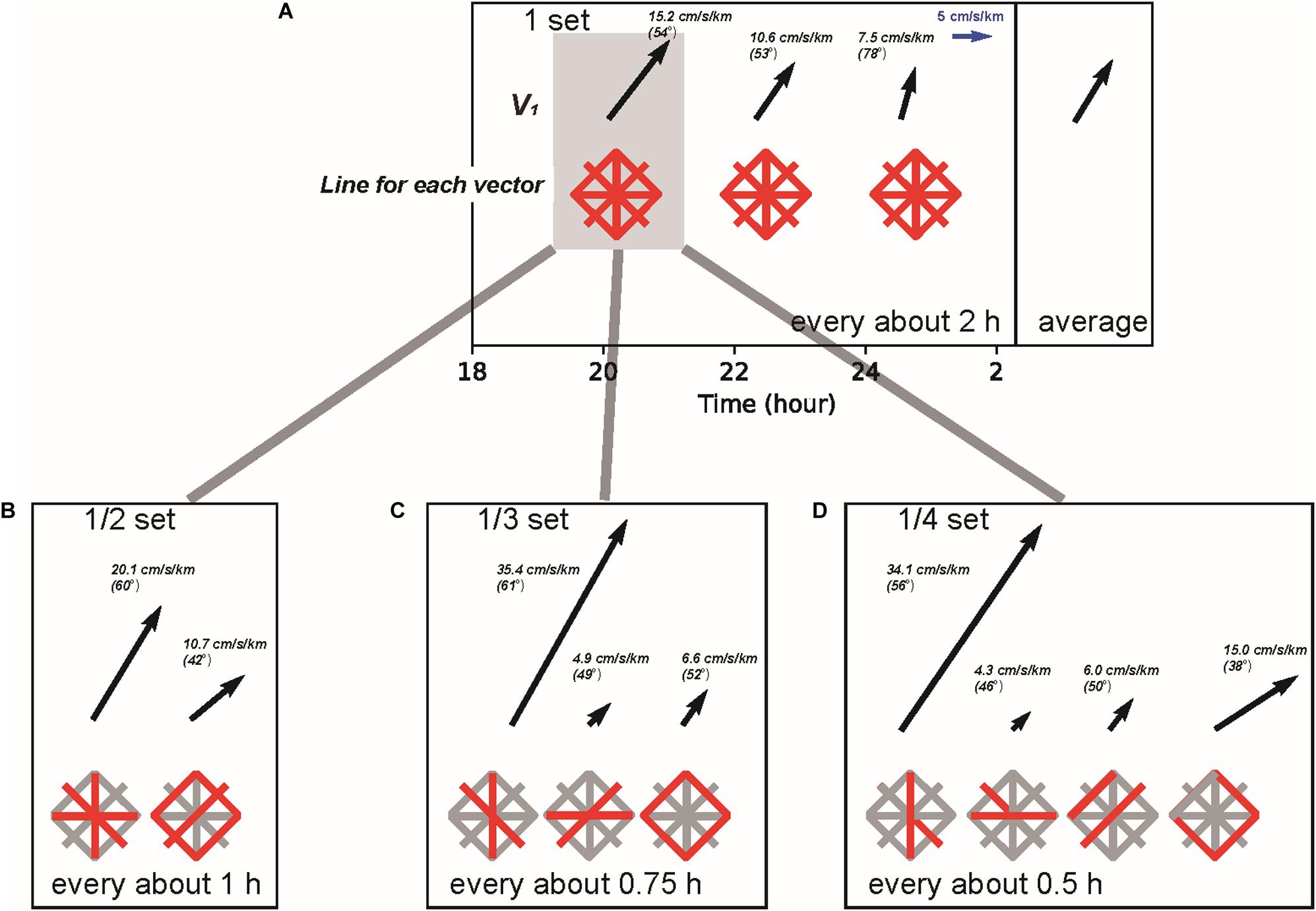
Figure 4. Time series of the gradient parameters of site MRT2 on November 23, 2018. The cases calculated for one set of survey lines (A; every about 2 h), divided into two parts (B; every about 1 h), divided into three parts (C; every about 0.75 h), and divided into four parts (D; every about 0.5 h), respectively. Each survey line (red line) shows the approximate line set for calculating each vector. The value of each vector (absolute value and counterclockwise angle from east) is written beside the vector.
Figure 4 shows that the gradient vectors become unstable as the coverage of the observation area becomes narrower. As shown in the layout of the survey lines, the estimation sensitivity is weak when the survey lines are perpendicular to the gradient, because the data coverage area in the direction of the gradient becomes narrower. In most cases, the SSS around site MRT2 has a meridional gradient since the flow of Kuroshio off the Kii channel is mainly eastward. Therefore, when the survey line covers only in the zonal direction (for example, in Figure 4D, second vector), a correct gradient cannot be detected.
From the above discussion, the time resolution of the GNSS-A estimated gradient vector for site MRT2 is about one hour at best, which is enough time to evenly cover the observation area. However, as with the case of spatial resolution, there is almost no model or in situ observation that can explain the hourly order fluctuations, making it difficult to verify whether the temporal variation of the estimated gradient vector reflects the actual underwater structure.
As shown in Figure 1B, the survey line length is set to be broadened depending on the depth so that the triangle size is large enough for stable estimation. Practically, the diagonal length of the survey lines is set to be approximately twice the depth of the site. Therefore, the observation time required to evenly cover all directions depends on the depth of the site. In the case of MRT2, whose depth is 1500 m, the time resolution is about one hour. Thus, the time resolution T at a site with an arbitrary depth is estimated as follows:
The time resolution derived from this relationship is about 2 h for a 3000 m depth site, and about 40 min for a 1000 m depth site. However, this is just a provisional result that needs to be confirmed by further research.
It is considered that the gradient SSSs off the Kii channel shown here reflects not only the large structures due to the Kuroshio but also fine scale fluctuations that are not easy to obtain appropriate data for comparison. In the future, further confirmation of the estimated gradient parameters will contribute not only to improve the accuracy of GNSS-A observations but also to assist the exploration of km-scale ocean fields that cannot be easily observed with the existing oceanographic methods. Since the GNSS-A observation network is deployed around Japan, we will proceed with discussions on regional differences and seasonal changes in features of km-scale structures that can be estimated by GNSS-A oceanography.
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: All data needed to evaluate the conclusions are present in the article. The XBT/XCTD underwater sound speed data is available in the PANGAEA website (Seafloor Geodesy Group et al., 2020; https://doi.pangaea.de/10.1594/PANGAEA.915138). Additional data related to this paper are available on request to the corresponding author. The JCOPE2M data is available in the JCOPE2M website (http://www.jamstec.go.jp/jcope/htdocs/e/home.html).
YY designed the study and wrote this manuscript. YY and TI led the direct observation of SSS. YY, TI, SW, and YN discussed about the analysis method and commented to improving the manuscript. All authors contributed to the article and approved the submitted version.
The submission of this manuscript was funded by the University of Tokyo.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We would like to thank the Geospatial Information Authority of Japan (GSI) for providing high-rate GNSS data for the kinematic GNSS analysis and daily coordinates of the GEONET sites (Sagiya et al., 2000; Nakagawa et al., 2009) on the GSI website. Many members of the staff of the Hydrographic and Oceanographic Department, Japan Coast Guard, including the crew of the survey vessels Takuyo, Shoyo, Meiyo, and Kaiyo, supported our observations and technological developments. We also thank for devoted maintenance and management by active and senior staffs in the Geodesy and Geophysics Office, Hydrographic and Oceanographic Department of Japan Coast Guard.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.00331/full#supplementary-material
FIGURE S1 | Residual time series of the travel time data for acoustic shots on observation dates, (a) June 3, 2013, (b) April 30, 2018, (c) July 6, 2018, and (d) November 23, 2018 for MRT1 and MRT2. Colored crosses and lines indicate residuals and average sound speeds for each station, respectively. After 1306, seafloor stations were replaced at MRT2. (A) Residual time series before corrections of V1 and V2. (B) Residual time series after corrections of V1 and V2. (C) Average sound speeds estimated before (gray) and after corrections of V1 and V2 (colored). (D) Time series of the vessel positions from the center (blue: eastward, red: northward).
Asada, A., and Yabuki, T. (2001). Centimeter-level positioning on the seafloor. Proc. Jpn Acad. Ser. B 77, 7–12. doi: 10.2183/pjab.77.7
Fujita, M., Ishikawa, T., Mochizuki, M., Sato, M., Toyama, S., Katayama, M., et al. (2006). GPS/acoustic seafloor geodetic observation: method of data analysis and its application. Earth Planet. Space 58, 265–275. doi: 10.1007/s00190-013-0649-9
Matsui, T., Kido, M., Niwa, Y., and Honsho, C. (2019). Effects of disturbance of seawater excited by internal wave on GNSS-acoustic positioning. Mar. Geophys. Res. 40, 541–555. doi: 10.1007/s11001-019-09394-6
Miyazawa, Y., Kuwano-Yoshida, A., Doi, T., Nishikawa, T., Narazaki, T., Fukuoka, T., et al. (2019). Temperature profiling measurements by sea turtles improve ocean state estimation in the Kuroshio-Oyashio Confluence region. Ocean Dyn. 69, 267–282. doi: 10.1007/s10236-018-1238-5
Miyazawa, Y., Varlamov, S. M., Miyama, T., Guo, X. T., Hihara, T., Kiyomatsu, K., et al. (2017). Assimilation of high-resolution sea surface temperature data into an operational nowcast/forecast system around Japan using a multi-scale three dimensional variational scheme. Ocean Dyn. 67, 713–728. doi: 10.1007/s10236-017-1056-1
Nakagawa, H., Toyofuku, T., Kotani, K., Miyahara, B., Iwashita, C., Kawamoto, S., et al. (2009). Development and validation of GEONET new analysis strategy (Version 4). J. Geograph. Surv. Inst. 118, 1–8.
Nakamura, Y., Noguchi, T., Tsuji, T., Itoh, S., Niino, H., and Matsuoka, T. (2006). Simultaneous seismic reflection and physical oceanographic observations of oceanic fine structure in the Kuroshio extension front. Geophys. Res. Lett. 33:L23605. doi: 10.1029/2006GL027437
Papenberg, C., Klaeschen, D., Krahmann, G., and Hobbs, R. W. (2010). Ocean temperature and salinity inverted from combined hydrographic and seismic data. Geophys. Res. Lett. 37:L04601. doi: 10.1029/2009GL042115
Ruddick, B., Song, H., Dong, C., and Pinheiro, L. (2009). Water column seismic images as maps of temperature gradient. Oceanography 22, 192–205. doi: 10.5670/oceanog.2009.19
Sagiya, T., Miyazaki, S., and Tada, T. (2000). Continuous GPS array and present-day crustal deformation of Japan. Pure Appl. Geophys. 157, 2303–2322. doi: 10.1007/PL00022507
Sato, M., Ishikawa, T., Ujihara, N., Yoshida, S., Fujita, M., Mochizuki, M., et al. (2011). Displacement above the hypocenter of the 2011 Tohoku-oki earthquake. Science 332:1395. doi: 10.1126/science.1207401
Seafloor Geodesy Group, Yokota, Y., and Ishikawa, T. (2020). Cross-section underwater sound speed observation data off the Kii Channel on November 23, 2018. PANGAEA doi: 10.1594/PANGAEA.915138
Spiess, F. N. (1985). Suboceanic geodetic measurements. IEEE Trans. Geosci. Remote Sensing GE 23, 502–510. doi: 10.1109/tgrs.1985.289441
Tsuji, T., Noguchi, T., Niino, H., Matsuoka, T., Nakamura, Y., Tokuyama, H., et al. (2005). Two-dimensional mapping of fine structures in the Kuroshio Current using seismic reflection data. Geophys. Res. Lett. 32:L14609. doi: 10.1029/2005GL023095
Watanabe, S., Sato, M., Fujita, M., Ishikawa, T., Yokota, Y., Ujihara, N., et al. (2014). Evidence of viscoelastic deformation following the 2011 Tohoku-oki earthquake revealed from seafloor geodetic observation. Geophys. Res. Lett. 41, 5789–5796. doi: 10.1002/2014GL061134
Yokota, Y. (2019). Quantitative interpretation of the ability of the GNSS-A to monitor underwater structure. J. Mar. Acoust. Soc. Jpn. 46, 116–129.
Yokota, Y., and Ishikawa, T. (2019). Gradient field of undersea sound speed structure extracted from the GNSS-A oceanography: GNSS-A as a sensor for detecting sound speed gradient. SN Appl. Sci. 1:693. doi: 10.1007/s42452-019-0699-6
Yokota, Y., and Ishikawa, T. (2020). Shallow slow slip events along the Nankai Trough detected by GNSS-A. Sci. Adv. 6:eaay5786. doi: 10.1126/sciadv.aay5786
Yokota, Y., Ishikawa, T., and Watanabe, S. (2018). Seafloor crustal deformation data along the subduction zones around Japan obtained by GNSS-A observations. Sci. Data 5:180182. doi: 10.1038/sdata.2018.182
Yokota, Y., Ishikawa, T., and Watanabe, S. (2019). Gradient field of undersea sound speed structure extracted from the GNSS-A oceanography. Mar. Geophys. Res. 40, 493–504. doi: 10.1007/s11001-018-9362-7
Keywords: GNSS-A, GNSS-A oceanography, sound speed structure, Kuroshio, Kii channel
Citation: Yokota Y, Ishikawa T, Watanabe S and Nakamura Y (2020) Kilometer-Scale Sound Speed Structure That Affects GNSS-A Observation: Case Study off the Kii Channel. Front. Earth Sci. 8:331. doi: 10.3389/feart.2020.00331
Received: 03 April 2020; Accepted: 16 July 2020;
Published: 04 August 2020.
Edited by:
Keiichi Tadokoro, Nagoya University, JapanReviewed by:
Shohei Minato, Delft University of Technology, NetherlandsCopyright © 2020 Yokota, Ishikawa, Watanabe and Nakamura. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yusuke Yokota, eXlva290YUBpaXMudS10b2t5by5hYy5qcA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.