Snowfall Fraction, Cold Content, and Energy Balance Changes Drive Differential Response to Simulated Warming in an Alpine and Subalpine Snowpack

Jennings, Keith S.; Molotch, Noah P.

doi:10.3389/feart.2020.00186

ORIGINAL RESEARCH article

Front. Earth Sci., 05 June 2020

Sec. Cryospheric Sciences

Volume 8 - 2020 | https://doi.org/10.3389/feart.2020.00186

Snowfall Fraction, Cold Content, and Energy Balance Changes Drive Differential Response to Simulated Warming in an Alpine and Subalpine Snowpack

$\nKeith S. Jennings,,,,$ Keith S. Jennings^1,2,3,4,5^*

Noah P. Molotch^4,5,6

¹Lynker, Boulder, CO, United States
²Department of Geography, University of Nevada, Reno, Reno, NV, United States
³Division of Hydrologic Sciences, Desert Research Institute, Reno, NV, United States
⁴Geography Department, University of Colorado Boulder, Boulder, CO, United States
⁵Institute of Arctic and Alpine Research, University of Colorado Boulder, Boulder, CO, United States
⁶NASA Jet Propulsion Laboratory, Pasadena, CA, United States

Despite widespread warming in mountain regions, little research to date has explored the physical mechanisms driving the variable response of snowpacks to changes in climate, instead focusing primarily on empirical relationships, such as seasonal air temperature or elevation. In this work, we evaluate how differences in snowfall fraction, cold content, and the snowpack energy balance produce simulated changes to snow accumulation and melt at an alpine and subalpine snowpack in the Niwot Ridge Long Term Ecological Research site. For our analysis, we created a 23 years baseline simulation using the SNOWPACK model forced by historical hourly meteorological data from water year 1991 through 2013. We then perturbed hourly air temperature in 0.5°C increments from +0.5 to +4.0°C above baseline and increased incoming longwave radiation accordingly. For every 1°C of warming, peak snow water equivalent declined by 43.9 mm in the alpine and 54.3 mm in the subalpine, melt onset shifted 6.2 days earlier in the alpine and 8.8 days in the subalpine, the snow season shortened by 10.7 days in the alpine and 16.4 days in the subalpine, and melt rate increased by 0.2 mm d⁻¹ in the alpine while decreasing by 0.4 mm d⁻¹ in the subalpine. We found the alpine snowpack was less sensitive to warming for three primary reasons: (1) Snowfall fraction decreased less rapidly per 1°C of warming than in the subalpine; (2) Cold content still consistently developed throughout the snow season, preventing mid-winter melt events; (3) Changes to snowmelt rate were not significant because increases to the turbulent fluxes balanced decreases in the radiative fluxes with earlier snowmelt onset. Additionally, at 3°C of warming and greater, the subalpine site experienced a fundamental shift where significant melt could occur throughout the entirety of the winter as cold content was no longer large enough to buffer against positive energy fluxes. In some years, the subalpine snowpack became transient with several cycles of accumulation and melt per winter. This tipping point suggests sites with lower cold content—like the subalpine studied here—are likely to be more sensitive to producing increased winter melt as warming continues over the coming decades.

Introduction

Climate warming has altered patterns of snow accumulation and melt throughout the seasonal snow zone in the western United States. Increasing winter air temperatures have led to a reduced percentage of precipitation falling as snow (Knowles et al., 2006) and decreased snow water equivalent (SWE) accumulation (Mote et al., 2005, 2018; Clow, 2010; Harpold et al., 2012). Many areas have also seen a shift to earlier snowmelt onset (Stewart et al., 2004; Regonda et al., 2005; Clow, 2010) and changes to seasonal melt patterns have impacted streamflow production (Regonda et al., 2005; Stewart et al., 2005; Stewart, 2009). Other implications of decreased snow cover in a warming world include changes to: the timing and magnitude of soil moisture fluctuations (Harpold and Molotch, 2015); soil temperature and microbial respiration (Brooks and Williams, 1999; Groffman et al., 2006; Blanken et al., 2009); forest greenness (Trujillo et al., 2012; Knowles et al., 2018); and water uptake and carbon sequestration by vegetation (Winchell et al., 2016). There is therefore considerable concern that future changes to snowpacks will have myriad impacts on mountain ecosystems worldwide (Gleeson et al., 2016).

Complicating matters is the non-linear response of mountain snowpacks to rising air temperatures across the mountainous western United States (Mote et al., 2005, 2018; Abatzoglou, 2011; Harpold et al., 2012; Kapnick and Hall, 2012; Harpold and Brooks, 2018). This has meant a unit increase in air temperature has not been associated with a spatially uniform change in various snowpack metrics, such as peak snow water equivalent (SWE), snowmelt onset, and snowmelt rate. Most previous work has ascribed the variability of the warming response to empirical factors, namely that snowpacks in middle elevations with winter air temperatures between −5 and 0°C have generally been more sensitive to warming than higher, colder sites (Knowles et al., 2006; Kapnick and Hall, 2012; Mote et al., 2018). Although such empirical relationships are useful for identifying areas susceptible to climate warming (e.g., Nolin and Daly, 2006), relatively little work has examined the physical controls governing the non-linear response.

Previous work of this nature has revealed several important relationships. Comparing sites with Mediterranean climates, López-Moreno et al. (2017) found that colder snowpacks tended to be less sensitive to warming than those with internal temperatures closer to 0°C. They also suggested that snowpacks with higher sensible heat fluxes would be more likely to see shifts in snowmelt due to warming than those with lower sensible heat fluxes. Krogh and Pomeroy (2019) related changes in snowmelt and decreases in snow cover duration to increases in all-wave irradiance associated with climate warming. Additionally, Musselman et al. (2017a) showed that earlier snowmelt is generally associated with a shift to reduced positive energy fluxes, but also that higher, colder sites are less sensitive to this shift. Quantifying the physical controls driving the non-linear response is therefore essential to better predicting the effect of increased air temperature on seasonal snow cover evolution.

According to the Intergovernmental Panel on Climate Change (IPCC), there is a high likelihood of warming continuing through the 21st century (IPCC, 2013). This is predicted to reduce snow accumulation and advance melt onset in areas that rely on mountain snowpacks for water resources (Barnett et al., 2005; Adam et al., 2009; Barnett and Pierce, 2009; Mankin et al., 2015). In the western United States, where over 60 million people depend on snowmelt for domestic, industrial, and agricultural purposes (Bales et al., 2006), significant temperature increases are likely to occur by century's end (e.g., Leung et al., 2004; USGCRP, 2017). This warming is expected to drive large-scale shifts from snow to rain across the region (Klos et al., 2014; Harpold et al., 2017b), which could reduce streamflow volume independent of changes to total precipitation (Berghuijs et al., 2014) and alter the spatial extent, frequency, and intensity of rain-on-snow events (Musselman et al., 2018). Furthermore, streamflow efficiency is sensitive to snowmelt rate with slower rates producing less streamflow per unit of precipitation than faster rates (Barnhart et al., 2016). Therefore, it is possible that predicted decreases to snowmelt rate with climate warming (Musselman et al., 2017a) will also reduce streamflow in snow-dominated areas.

It has also been shown that the non-linear response of mountain snowpacks to increasing air temperatures will likely continue with further warming (Klos et al., 2014; Luce et al., 2014; Cooper et al., 2016; Musselman et al., 2017a,b). Within this body of previous research, there is a need to investigate the physical processes controlling the differential responses of more/less sensitive snowpacks to changes in climate. In this context, the Niwot Ridge Long Term Ecological Research (LTER) site offers a unique opportunity to evaluate such processes. The LTER has long-term snow pit and meteorological measurements from a subalpine location likely to be more sensitive to warming as well as from a less sensitive colder, higher alpine location. This study leverages the historical data from these sites along with a physics-based snow model and a range of air temperature scenarios to answer two research questions:

1) Do the alpine and subalpine snowpacks exhibit differential responses in snow accumulation and melt to increases in air temperature?

2) How do differences in the responses of snowfall fraction, cold content, and the snowpack energy balance affect the response to climate warming?

Study Site and Data

This study utilized long-term meteorological and snow pit records from two sites within the Niwot Ridge LTER on the eastern slope of the Continental Divide in Colorado's Rocky Mountains (Figure 1). The alpine and subalpine sites are respectively located at 3,528 and 3,022 m a.s.l., with treeline occurring at ~3,400 m a.s.l. High winter wind speeds, averaging 10–13 m s⁻¹, control snow deposition patterns in the alpine (Erickson et al., 2005; Litaor et al., 2008; Jepsen et al., 2012), while a dense canopy of lodgepole pine intercepts falling snow and reduces turbulent fluxes in the subalpine (e.g., Molotch et al., 2007). Further details on differences in site physiography and snow accumulation and melt can be found in Jennings et al. (2018a).

FIGURE 1

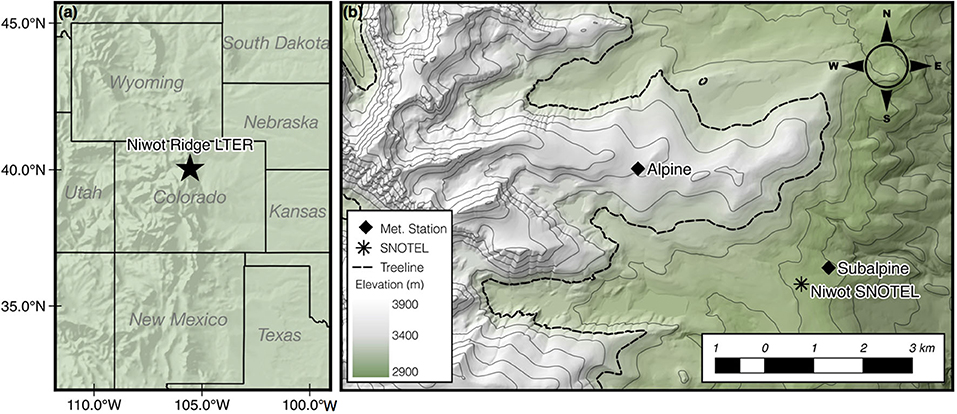
Figure 1. The location of the Niwot Ridge LTER within the western United States (A) and a topographical map showing the co-located meteorological stations and snow pit sites as well as the Niwot Snowpack Telemetry (SNOTEL) station. The dashed line in the LTER inset (B) represents approximate treeline (3,400 m a.s.l.) and the thin, solid lines are 100 m contours.

For our study, the alpine site was representative of a snowpack likely to be less sensitive to climate perturbations, while the subalpine was potentially more sensitive. This was based on how December, January, and February (DJF) average air temperatures at the two sites compared to previous work, which has shown the largest sensitivity to warming occurs between approximately −5 and 0°C (Knowles et al., 2006; Kapnick and Hall, 2012; Mote et al., 2018). Over the baseline historical period (1 October 1991 through 30 September 2013), average DJF air temperature was −10.3°C in the alpine and −6.2°C in the subalpine (Table 1).

TABLE 1

Table 1. Mean meteorological quantities for December, January, and February (DJF) at the alpine and subalpine sites (WY1991–WY2013) along with mean peak SWE magnitude and timing for the two sites as observed in the snow pits (WY2007–WY2013).

Meteorological data were available from water year 1991 (WY, 1 October of the previous calendar year to 30 September) to WY2013. These data included hourly observations of air temperature, relative humidity, wind speed, incoming shortwave radiation, and precipitation. The raw observations were subjected to an intensive quality control and infilling procedure to ensure their suitability as model forcing data (Jennings et al., 2018a). The serially complete records of air temperature, relative humidity, and incoming shortwave radiation were used to calculate an empirical estimate of incoming longwave radiation based on the recommendations of Flerchinger et al. (2009). The complete dataset and metadata are publicly available from the LTER network (Jennings et al., 2017).

The alpine and subalpine sites also have long-term snow pit records of SWE, snowpack temperature, and other properties (Williams et al., 1999; Williams, 2016). The record includes 292 snow pit measurements from WY1995–WY2013 in the alpine and 147 measurements from WY2007–WY2013 in the subalpine. The snow pit data were used to validate simulated snow cover properties and to improve the forcing data, namely precipitation corrections for gage under-/over-catch, as well as to parameterize the canopy module for the subalpine model runs as detailed in Jennings et al. (2018a). We also validated modeled subalpine SWE using automated SWE data from the Niwot Snow Telemetry (SNOTEL) station, which is located within the Niwot Ridge LTER <1 km from the subalpine site at an elevation of 3,021 m a.s.l. (Figure 1).

Methods

SNOWPACK Model Description

SNOWPACK is a physics-based snow model forced by air temperature, relative humidity, wind speed, incoming shortwave and longwave radiation, and precipitation at an hourly or shorter time step (Bartelt and Lehning, 2002; Lehning et al., 2002a,b). The model simulates a one-dimensional snowpack with an infinite number of layers that have their own thickness, density, and temperature values, as well as snow grain size and type. New layers are added with snowfall, while melt and densification lead to a reduction in the number of layers. As a multi-layer model, SNOWPACK allows the production of surface melt that can be refrozen in colder lower layers during appropriate meteorological and snowpack conditions. SNOWPACK also provides a full treatment of the snowpack energy balance:

\begin{array}{l} \frac{d U}{d t} + Q_{M} = Q_{S W} + Q_{L W} + Q_{H} + Q_{L E} + Q_{G} + Q_{R} & (1) \end{array}

where $\frac{d U}{d t}$ is the simulated rate of change in internal snowpack energy, Q_M is the energy available for snowmelt (i.e., the latent heat of fusion times the mass lost per second to snowmelt), Q_SW is net shortwave radiation, Q_LW is net longwave radiation, Q_H is sensible heat flux, Q_LE is latent heat flux, Q_G is ground heat flux, and Q_R is the heat advected by precipitation (all W m⁻²).

Model configuration was the same as in Jennings et al. (2018a) except this study used SNOWPACK version 3.4.5 in place of version 3.3.0, which was used in the previous work. Additionally, we changed the way precipitation phase partitioning was handled by the model. Unless precipitation phase is assigned in the forcing data file, SNOWPACK calls the data preprocessor MeteoIO (Bavay and Egger, 2014) to designate whether the precipitation is rain, snow, or a mix of the two. In its standard configuration, the user indicates whether MeteoIO should use either a single air temperature threshold to partition rain and snow or a range between two air temperature values with a linear mix of precipitation phase in between. For this work, we updated MeteoIO to include a binary logistic regression model (e.g., Froidurot et al., 2014; Jennings et al., 2018b) that partitions precipitation between rain and snow as a function of air temperature and relative humidity:

\begin{array}{l} p (s n o w) = \frac{1}{1 + e^{(α + β T_{a} + γ R H)}} & (2) \end{array}

where p(snow) is the probability of snow (0–1, dimensionless), α, β, and γ are the optimized model coefficients (−10.04, 1.41, and 0.09, dimensionless), T_a is air temperature (°C), and RH is relative humidity (%). Precipitation is set to be snow when p(snow) ≥ 0.5 and rain when p(snow) < 0.5. The binary logistic regression model was shown to be the most effective method in a Northern Hemisphere comparison (Jennings et al., 2018b) and it produces low biases in modeled SWE (Jennings and Molotch, 2019).

SNOWPACK was chosen for this work because the model has been extensively validated in the literature in terms of its ability to represent SWE, snow depth, snowpack temperature, cold content, snow microstructure, and energy balance partitioning (Lehning et al., 2001; Lundy et al., 2001; Etchevers et al., 2004; Rutter et al., 2009; Meromy et al., 2015; Jennings et al., 2018a). In addition, SNOWPACK and its spatially distributed version, Alpine3D (Lehning et al., 2006), have been effectively used to explore the effect of climate change on snow cover properties in various areas with differing physiographic and climatic properties (Rasmus et al., 2004; Bavay et al., 2013; Meromy et al., 2015; Marty et al., 2017; Musselman et al., 2017b).

Baseline Model Runs

We used the model setup described in the section above and the quality controlled forcing data from Jennings et al. (2018a) to simulate the alpine and subalpine snowpacks for the period WY1991–WY2013. Simulated SWE, depth-weighted snowpack temperature (i.e., the average snowpack temperature where each layer's temperature is weighted by its depth), and cold content for the baseline (i.e., historical) runs were validated on the equivalent snow pit and SNOTEL observations. The switch to SNOWPACK 3.4.5 yielded a negligible change in performance as measured by the coefficient of determination (r²) and mean bias (Table 2) relative to version 3.3.0 used in Jennings et al. (2018a).

TABLE 2

Table 2. Validation metrics for the baseline simulations compared to snow pit SWE, depth-weighted temperature (T_s), and cold content data in the alpine and snow pit plus SNOTEL data in the subalpine.

Air Temperature and Incoming Longwave Radiation Perturbations

The baseline simulations were perturbed based on a range of predicted likely changes to air temperature in the southwestern United States and Colorado as presented in the US Global Change Research Program's (USGCRP) Fourth National Climate Assessment (USGCRP, 2017) and a statewide climate report (Lukas et al., 2014). These reports utilize output from a suite of climate models from the third and fifth phases of the Coupled Model Intercomparison Project (CMIP3 and CMIP5) and details on the methods can be found within the source documents. The USGCRP projects annual air temperature in the southwestern United States may increase by between 2.1 and 2.7°C in RCP4.5 and RCP8.5 by mid-21st century (Vose et al., 2017), with the Colorado report projecting between 1.4 and 3.6°C of warming depending on RCP scenario (Lukas et al., 2014). These projections are in line with mid-century warming predicted for the Rocky Mountains in the recent IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (SROCC, Hock et al., 2019). For our snow modeling, we used the delta-change approach and applied air temperature increases in 0.5°C increments from +0.5 to +4.0°C. Each increase was applied uniformly to the baseline hourly data and we did not consider seasonal changes to air temperature or impacts to the diurnal temperature range.

In addition to increasing air temperature, we also increased incoming longwave radiation through the Stefan-Boltzmann law:

\begin{array}{l} L W_{i n} = σ ε_{a} T_{a}^{4} & (3) \end{array}

where LW_in is incoming longwave radiation (W m⁻²), σ is the Stefan-Boltzmann constant (5.67 × 10⁻⁸ W m⁻² K⁻⁴), ε_a is atmospheric emissivity (0–1, dimensionless), and T_a is air temperature (K). In the empirical equations we used to compute LW_in, ε_a was estimated as a function of humidity and cloud cover inferred from solar radiation (Jennings et al., 2018a). In our perturbations, we kept hourly ε_a values from the baseline scenario constant due to the high uncertainty in future humidity and cloud cover (IPCC, 2013).

Assessing Changes to Snow Accumulation and Melt, Snowfall Fraction, Cold Content, and the Snowpack Energy Balance

With regard to the first research question, we analyzed the SNOWPACK output data from the climate change simulations to look for evidence of a differential response between the snowpacks at the two sites. We used a set of four snowpack metrics designed to capture seasonal snow cover evolution:

1) Peak SWE: The total water stored in the snowpack at its maximum.

2) Melt onset (i.e., the date of peak SWE): Although melt may occur before the date of peak SWE, this metric is often used as the timing of melt onset as it signifies the start of the main snowmelt period in seasonal snowpacks.

3) Snowmelt rate: The average snowmelt rate between melt onset and the first date of SWE = 0 mm.

4) Snow-covered days: The total number of days with SWE > 0 mm.

The first three metrics above are of interest to water managers as they represent how much, when, and at what rate meltwater will be produced. The last metric is important to the earth's climate as snow has a higher albedo than bare ground, meaning a greater proportion of incoming solar radiation is reflected when snow is on the ground.

After analyzing the output data for evidence of a differential response of the two snowpacks, we then focused on research question two by assessing three components of physical control: (1) snowfall fraction—the proportion of annual precipitation falling as snow, (2) cold content, and (3) the snowpack energy balance. In this work snowfall fraction was considered a primary response driver as it represents the amount of rain or snow entering the snowpack or bare ground if no snow cover was present. This is critical given the differing effects rain and snow have on snowpack properties and land surface hydrology. The next component we considered was cold content, which is a measure of the snowpack's energy deficit:

\begin{array}{l} C C = c_{i} ρ_{s} d_{s} (T_{s} - T_{m}) & (4) \end{array}

where CC is snowpack cold content (MJ m⁻²), c_i is the specific heat of ice (2.1 × 10⁻³ MJ kg⁻¹ °C⁻¹), ρ_s is the density of snow (kg m⁻³), d_s is snow depth (m), T_s is the depth-weighted snowpack temperature (°C), and T_m is the melting temperature of ice (0°C). We expected cold content to be impacted by the perturbations because the cold content of new snowfall is simulated as a linear function of air temperature and precipitation (Wigmosta et al., 1994; Lehning et al., 2002a; Cherkauer et al., 2003). At our sites, previous work has shown snowfall to be the primary pathway of cold content development, with negative surface energy fluxes contributing to a lesser degree (Jennings et al., 2018a). Finally, we analyzed changes to the snowpack energy balance (Equation 1) that occurred with the climate perturbations. Q_SW is generally the prime source of melt energy in mountain snowpacks (e.g., Marks and Dozier, 1992; Cline, 1997; Bales et al., 2006; Jepsen et al., 2012), while Q_LW, Q_H, and Q_LE can also contribute significantly depending on the tree cover and climate of a given site (Moore and Owens, 1984; Garvelmann et al., 2014; Jennings and Jones, 2015; Würzer et al., 2016; Mott et al., 2018). For this part of the analysis we did not include Q_G and Q_R as they contributed near-negligible amounts of energy to Q_M in the baseline and climate change scenarios.

Results

Differential Changes to Snow Accumulation and Melt

SWE accumulation decreased at both sites with air temperature increases, but the sites exhibited a differential response to warming (Figure 2, Table 3). The subalpine site was more sensitive to the ΔT perturbations, with mean peak SWE declining 15.4% °C⁻¹ as compared to 4.9% °C⁻¹ in the alpine. The loss of snow-covered days and the progression of melt onset per degree of warming were also more pronounced in the subalpine. For example, an increase of 2°C was associated with a loss of 32.8 days in annual snow cover duration relative to the baseline in the subalpine and 21.4 days in the alpine, a relative difference of 53.3%. Similarly, subalpine melt onset advanced by 2.6 more days per 1°C of warming than alpine melt onset. Daily snowmelt rate also declined significantly in the subalpine, while the alpine increase was not significant at the 95% level. Changes to snowmelt rate in the ΔT perturbations will be discussed further in the energy balance results section below (section The Role of the Snowpack Energy Balance During Snowmelt).

FIGURE 2

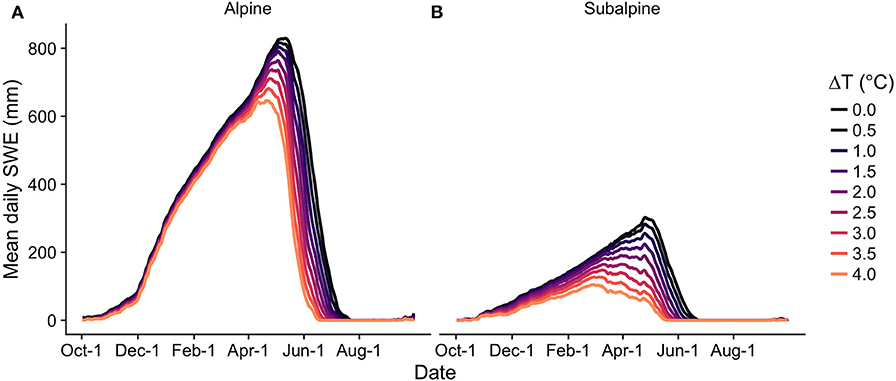
Figure 2. Mean daily modeled SWE for the baseline and warming simulations in the alpine (A) and subalpine (B).

TABLE 3

Table 3. Changes to mean snow accumulation and melt metrics associated with the baseline (WY1991–WY2013) and climate warming scenarios.

Changes to Snowfall Fraction

The ΔT perturbations had a significant effect on snowfall fraction at the two sites (Figure 3). In the alpine, mean snowfall fraction declined from 83.9% in the baseline simulation to 74.8% with the +4.0°C warming scenario, while subalpine snowfall fraction decreased from 71.0% in the baseline to 54.7% in the greatest warming scenario. This meant, on average, the alpine saw total annual snowfall decline from 1,167 ± 239 mm in the baseline to 1,042 ± 211 mm in the +4.0°C perturbation. Similarly, the subalpine declined from 527 ± 115 mm of annual snowfall in the baseline to 407 ± 92 mm with 4.0°C of warming. In terms of sensitivity to warming, the subalpine site was more sensitive, exhibiting a 5.7% °C⁻¹ reduction in snowfall fraction, compared to 2.7% °C⁻¹ in the alpine.

FIGURE 3

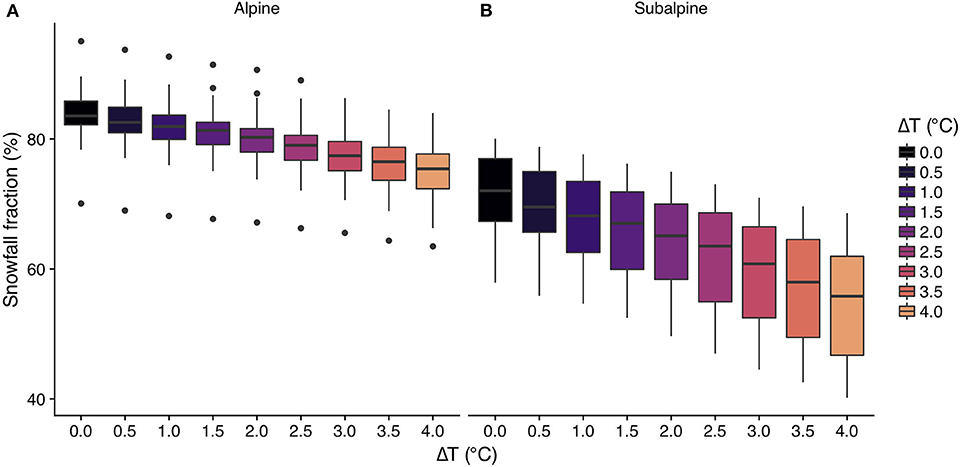
Figure 3. Annual snowfall fraction for the baseline and ΔT perturbations in the alpine (A) and subalpine (B) for the 23 simulation years. Boxplots show the median, interquartile range, and outliers for the annual snowfall fraction.

Cold Content

Seasonal patterns of cold content development and removal were significantly impacted by the ΔT perturbations (Figure 4, Table 4). In the subalpine, average annual peak cold content was reduced by more than half for the +4.0°C scenario relative to the baseline, declining to −0.6 MJ m⁻² from −1.5 MJ m⁻². Average annual alpine peak cold content was less affected in relative terms by the ΔT perturbations, declining from −6.1 MJ m⁻² in the baseline to −4.1 MJ m⁻² in the +4.0°C warming scenario, a loss of 32.7%. In absolute terms, the alpine saw a greater MJ m⁻² decline per 1°C of warming. This was likely due to the fact that the subalpine snowpack goes isothermal several times throughout the winter (i.e., cold content equals zero), even in the baseline. This meant the alpine had a greater absolute range in which its cold content could be reduced by warming.

FIGURE 4

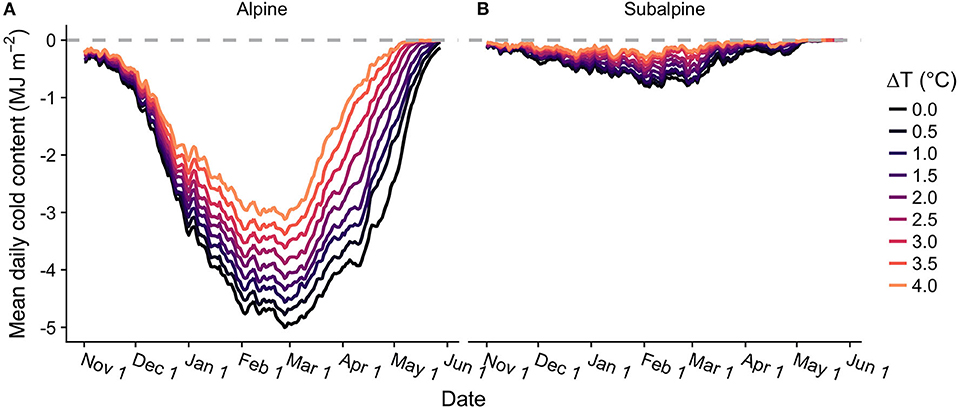
Figure 4. Same as Figure 2 but for mean daily cold content.

TABLE 4

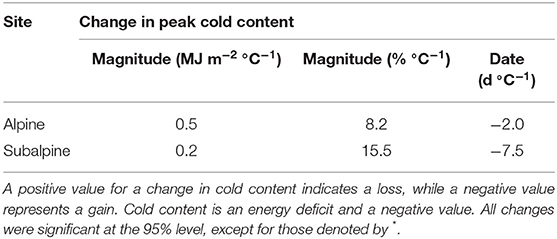
Table 4. Same as Table 3, but values correspond to changes in cold content.

Changes to seasonal patterns of cold content development and removal in the ΔT perturbations were a direct result of changes in the cold content added to the snowpack per day during snowfall (Figure 5). For the baseline scenario, each 50 mm of daily snowfall was responsible for, on average, −1.0 MJ m⁻² of cold content additions to the alpine snowpack and −0.6 MJ m⁻² to the subalpine snowpack, reflecting air temperature differences between the sites. Each 1°C of warming was associated with a loss of 0.05 MJ m⁻² of cold content for every 50 mm of daily snowfall. This meant the cold content added to the snowpack by each 50 mm of snowfall fell to −0.9 MJ m⁻² in the alpine and −0.5 MJ m⁻² in the subalpine with 2°C of warming. Across the entire snow season, new snowfall added an average of −22.1 MJ m⁻² of cold content in the alpine and −5.8 MJ m⁻² in the subalpine. These totals declined by 9.9 and 13.0%, respectively, with each 1°C of warming at the two sites, meaning each site required less total energy to warm and melt the entire snowpack.

FIGURE 5

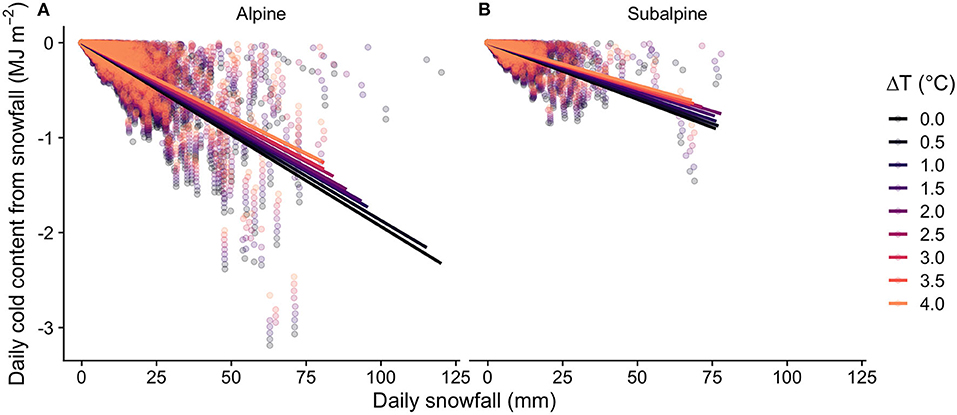
Figure 5. Daily cold content additions from snowfall plotted against daily snowfall for the ΔT perturbations in the alpine (A) and subalpine (B). The solid lines of best fit were computed using ordinary least squares regression and show a decrease in cold content from snowfall with increasing air temperatures (all p-values < 0.0005).

The Role of the Snowpack Energy Balance During Snowmelt

As noted above, the warming scenarios significantly reduced melt rates in the subalpine, while the increases to alpine melt rate were not statistically significant at the 95% level. This was caused by a significant decrease in melt-period Q_M in the subalpine with warming and a non-significant increase in the alpine (Figures 6A,B). At both sites, the ΔT perturbations produced earlier snowmelt timing (Figure 2, Table 3), which led to a decrease in the net radiative fluxes (Figures 6C,D). This decline was primarily a result of reduced incoming solar radiation as the melt period shifted earlier in the year away from the summer solstice (i.e., away from when solar zenith angles are lowest and day lengths are greatest). The advance of snowmelt timing with warming also decreased Q_LW as melt-period air temperatures decreased with the larger ΔT perturbations. This may appear counter-intuitive, but the shift in melt timing had a greater effect on melt-period air temperatures and the resultant incoming longwave radiation than the applied warming. Furthermore, an increase in the turbulent fluxes balanced the decrease in the radiative fluxes in the alpine, an effect not simulated in the subalpine where the turbulent fluxes increased only 1.8 W m⁻² from the baseline to the +4.0°C scenario (Figures 6E,F). On average, Q_H and Q_LE were ~10× greater in the alpine than subalpine because forest cover significantly damped wind speeds and the turbulent fluxes at the snow surface at the latter site.

FIGURE 6

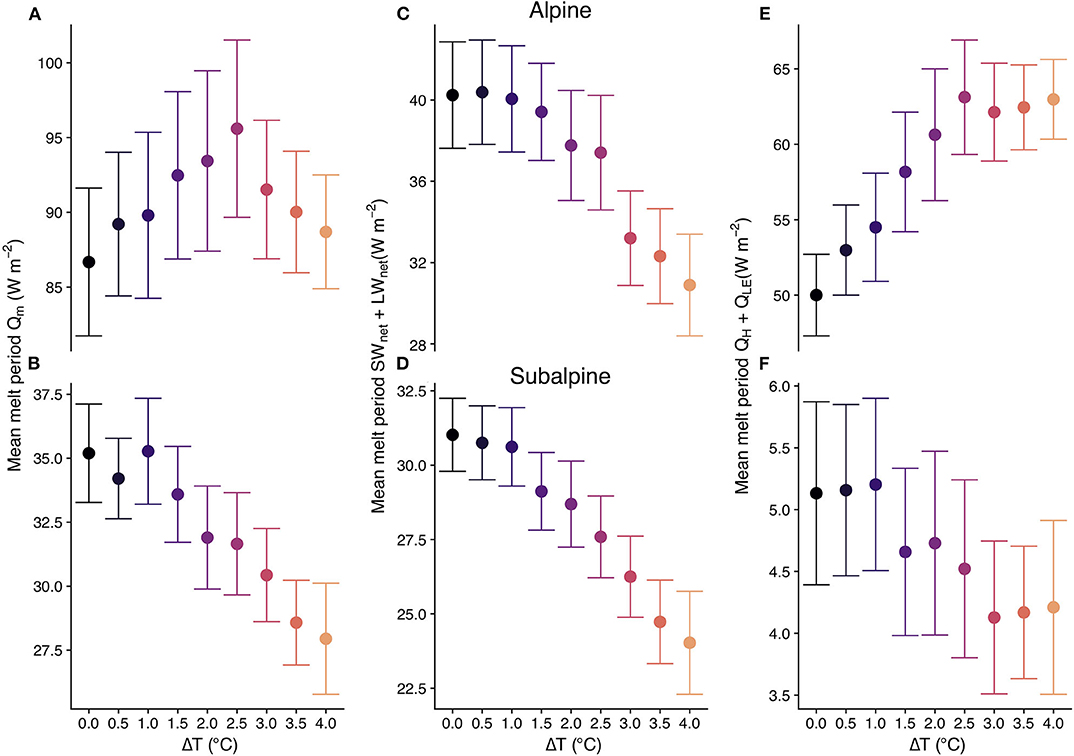
Figure 6. Mean melt period Q_M (A,B), radiative fluxes (C,D), and turbulent fluxes (E,F) in the alpine (top) and subalpine (bottom). Here the melt period is defined as the time between peak SWE and the snow-off date. The points are the average hourly flux value across the melt periods from the 23 simulation years with whiskers representing ±1 standard error for each ΔT scenario. Note: y-axis ranges are different for each subplot.

Notably, the alpine snowpack experienced the greatest melt-period Q_M and turbulent fluxes at +2.5°C of warming. This was related to the progression of alpine melt onset in the warming scenarios. For every 0.5°C warming increment except for +2.5 to +3.0°C, the average shift in melt onset was 2.4 days earlier. For the +2.5 to +3.0°C warming increment, the shift was 6.1 days earlier, the largest jump of all the warming increments. Additionally, all warming increments were associated with a slight increase in wind speed, going from 6.5 m s⁻¹ in the baseline to 7.2 m s⁻¹ at +4.0°C. From the baseline scenario to +2.5°C of warming, melt-period air temperature stayed within ±0.1 of 5°C. At +3°C of warming, melt period air temperature decreased to 4.6°C. These factors, not seen in the subalpine, were responsible for the shape of the Q_M and turbulent flux curves, as well as the slight increase in snowmelt rate at the alpine site.

Increased Winter Melt: Interactions Between Cold Content and the Snowpack Energy Balance

Figure 7 displays the average daily cold content plus the average net flux (i.e., the sum of the flux terms on the righthand side of Equation (1) plus the cold content added from snowfall) into the snowpack for the different warming scenarios. In this figure, a colored line plotted beneath the horizontal gray zero line indicates the net flux was not great enough, on average, to satisfy the cold content for that day. Conversely, a colored line above the zero line indicates that, on average, the net flux was greater than cold content and melt could occur. The alpine and subalpine express divergence in where the colored lines cross the horizontal zero line, which is reflective of the physical processes controlling the differential response of the two sites to warming air temperatures. Both snowfall fraction and the cold content of new snowfall were reduced in the ΔT perturbations, meaning it took less energy to satisfy the snowpack's internal energy deficit. This was compounded by the fact that the net radiative and turbulent fluxes were greater throughout the snow cover season for the warmer ΔT perturbations. For example, DJF and MAM (March, April, May) net fluxes were respectively 2.0 and 27.8 W m⁻² greater in the alpine and 1.8 and 8.1 W m⁻² greater in the subalpine for the +4.0°C scenario relative to the baseline.

FIGURE 7

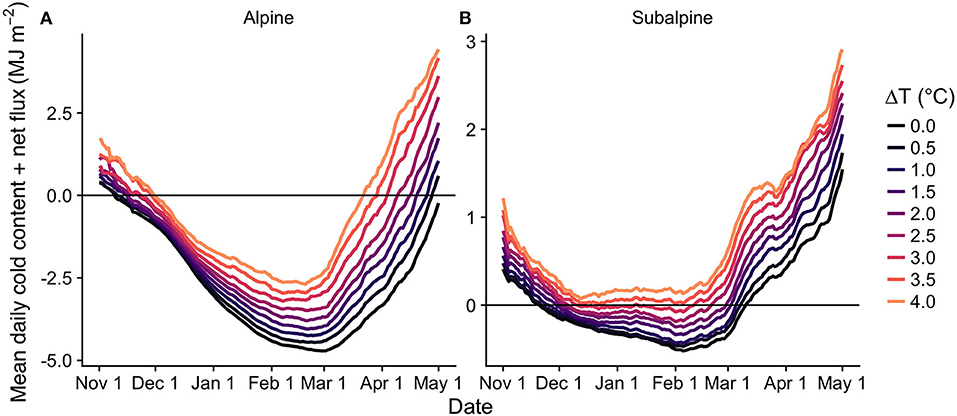
Figure 7. Mean daily cold content plus net flux (i.e., the sum of the energy fluxes on the righthand side of Equation 1 plus the cold content added from snowfall) for the ΔT perturbations in the alpine (A) and subalpine (B). The black horizontal line at 0 MJ m⁻² represents cold content being equal to the net fluxes in magnitude. Colored lines above the zero line indicate that the net fluxes were, on average, greater in magnitude than snowpack cold content, meaning melt could occur. Note: subplots have different y-axis ranges in order to see line spread in subalpine.

For the +3.0°C and greater warming scenarios, daily average cold content was no longer greater than daily average net flux in the subalpine (Figure 7B), meaning melt was probable throughout the entirety of the snow cover season. This shift led to a marked increase in the number of winter melt events, with total annual average pre-peak SWE melt approximately doubling from 71.7 mm in the baseline to 146.6 mm in the +4.0°C scenario (Figure 8). This meant pre-peak SWE melt increased proportionally from 20.3% of peak SWE in the baseline to 97.6% in the warmest ΔT perturbation. Thus, the amount of water lost to melt during the winter nearly equaled the total water stored in the snowpack at peak SWE with 4.0°C of warming. In some simulation years for the three warmest ΔT perturbations, subalpine snow cover shifted from seasonal to transient (i.e., ephemeral), representing a substantial shift in the hydrology of the subalpine snowpack. Conversely, winter melt stayed minimal in the alpine relative to the subalpine, reaching a maximum annual average of 52.8 mm (7.0% of peak SWE) in the +2.5°C scenario. This was likely due to the same large shift in melt onset noted in the results section above from the +2.5 to +3.0°C scenario. In some simulation water years, melt onset occurred markedly later in the former compared to the latter. For example, in WY1995, melt onset occurred 19 days later at +2.5°C compared to +3.0°C. In this extended pre-peak SWE period, an additional 182 mm of modeled snowmelt occurred in the +2.5°C scenario.

FIGURE 8

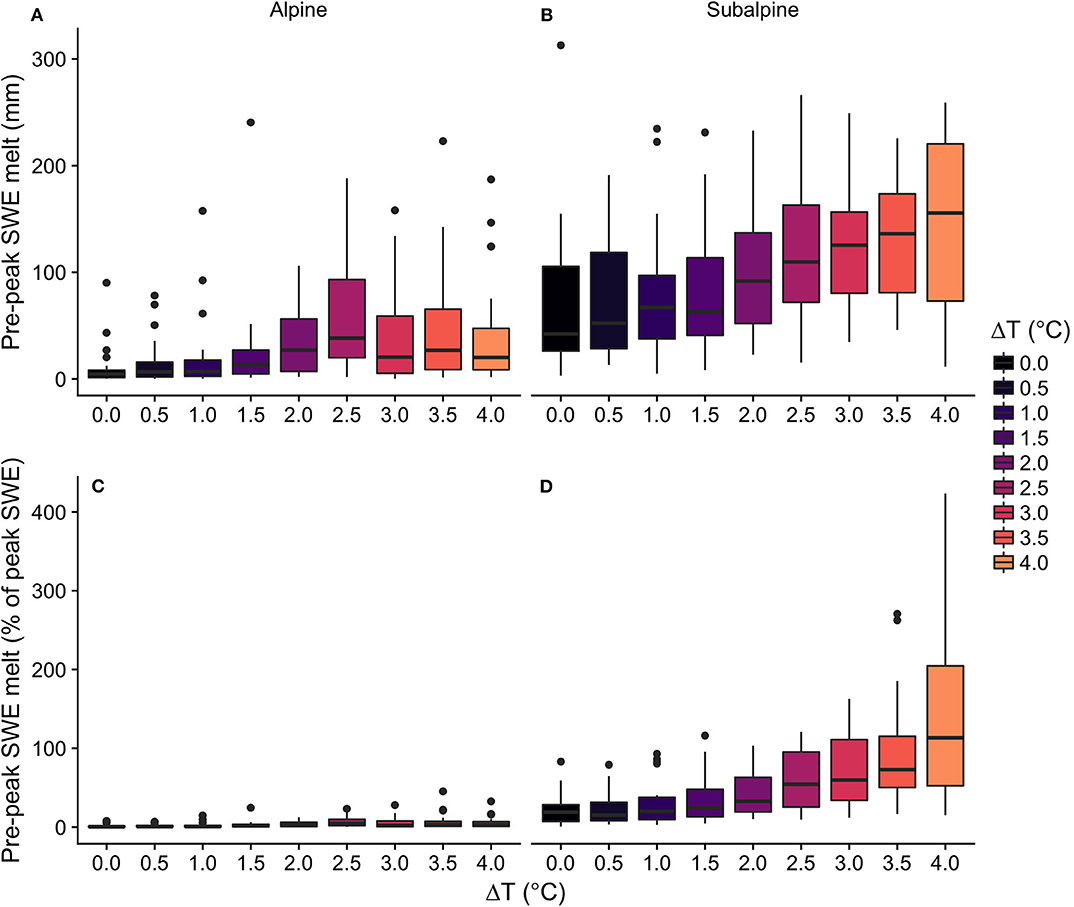
Figure 8. Total snowmelt before peak SWE presented as a depth (A,B) and as a percentage of peak SWE (C,D) in the alpine (left column) and subalpine (right column).

Discussion

Physical Controls on the Differential Response

Previous research has shown colder sites at higher elevations have been less sensitive than lower, warmer ones to the effects of climate warming on snow accumulation and melt (Harpold et al., 2012; Kapnick and Hall, 2012; Mote et al., 2018). In general, sites with air temperatures closer to 0°C have more precipitation falling near the freezing point, making decreases in snowfall fraction more likely (e.g., Knowles et al., 2006). Those with colder snowpacks are typically less sensitive to simulated warming, while a larger contribution of turbulent fluxes to the snowpack energy budget may make a site more sensitive (López-Moreno et al., 2017). Simulations also show that higher, colder sites are less sensitive to changes in the snowpack energy balance and snowmelt rate (Musselman et al., 2017a).

At both our study sites, warming led to decreases in peak SWE, earlier snowmelt onset, and reduced snow cover duration. Overall, we found the higher, colder alpine site to be less sensitive to the effects of warming air temperatures on snow accumulation and melt. This can be explained through differences in the physical factors we evaluated in the results sections above, namely the interaction of snowfall fraction, cold content, and the snowpack energy balance. From a first-order perspective, snowfall fraction at the alpine site was reduced by a lesser percentage with each degree of warming relative to the subalpine (Figure 3). This meant that frequent snowfall persisted in the alpine despite air temperature increasing by the same amount as in the subalpine. Notably, new snowfall is the primary means of cold content development at our two study sites, while contributions from negative energy fluxes tend to be small (Jennings et al., 2018a). Warmer air temperatures also reduced the amount of cold content added to the snowpack per snowfall event (Figure 5) as the cold content of new snowfall is estimated as a linear function of air temperature and precipitation. This loss of cold content from snowfall was, in turn, compounded by gains in DJF and MAM energy fluxes to the snowpack as a result of warming.

This chain of events led to the situation where there was both more energy available to warm and melt the snowpack and a lower energy deficit that needed to be satisfied to raise the snowpack internal temperature to an isothermal 0°C. As a site with higher winter air temperatures and lower snowfall to begin with, the subalpine snowpack had less peak annual cold content in the baseline simulations than the alpine. As warming progressed, the disparity became greater, with average annual peak cold content approaching just −0.4 MJ m⁻² in the subalpine and −3.0 MJ m⁻² in the alpine in the +4.0°C scenario. The significantly diminished subalpine cold content—i.e., approaching 0 MJ m⁻²–made the site more prone to midwinter melt events, which reduced peak SWE accumulation as mass was lost to melt before the main snowmelt season. Conversely, even with the same amount of simulated warming, cold content still developed consistently in the alpine snowpack, which helped buffer against warming-caused increases in positive energy fluxes.

Importantly, at 3°C of warming and above, the subalpine snowpack was substantially altered by a shift in the melt season from spring to the entirety of the winter. In some years, the snowpack became transient, with several cycles of accumulation and melt per winter. No longer was cold content large enough to buffer against midwinter melt. Instead, melt was probable and likely throughout the entirety of the snow cover season. From a hydrologic perspective, this would mean meltwater delivery to the soil will occur earlier as warming progresses, which may have marked impacts of streamflow and water uptake by vegetation (e.g., Rasouli et al., 2014, 2015; Krogh and Pomeroy, 2019). This is of concern considering 3°C of warming is within the range of projected mid-century air temperature increases used in this study and well inside projected end-of-century increases reported by the USGCRP (Vose et al., 2017) and in the SROCC (Hock et al., 2019). Predicted warming could therefore have profound impacts on water resources availability through its effects on snowfall fraction and the snowpack energy budget, particularly in areas where peak cold content values are already near 0 MJ m⁻².

In addition to the physical processes examined in this work, it is also important to note the seasonal evolution of subalpine snowpacks is strongly controlled by the interactions between forest characteristics and climate (Molotch et al., 2009; Lundquist et al., 2013; Dickerson-Lange et al., 2017; Roth and Nolin, 2017). Forest cover, among other physiographic properties, can also affect the response of a subalpine snowpack to changes in air temperature (Tennant et al., 2017). At our study sites, forest cover in the subalpine was associated with decreased Q_SW, increased Q_LW, and decreased turbulent fluxes relative to the alpine. Such low turbulent flux values are common to sheltered subalpine sites (Molotch et al., 2007; Marks et al., 2008). Both Q_LW and the turbulent fluxes respond positively to higher air temperatures, while any slight increases to Q_SW are due to albedo reductions caused by more rapid snow grain growth. Thus, from an energy balance perspective, the subalpine expressed increased melt primarily due to Q_LW, while increased turbulent fluxes did the same in the alpine. Despite the alpine fluxes increasing by a greater amount in DJF and MAM, the site was less sensitive because it received greater cold content than the subalpine, which acted as a buffer against positive energy fluxes.

Implications for Water Resources Management in a Warming Climate

Climate change poses a serious challenge to water resources management through its effects on the timing and volume of water deliveries to reservoirs and other infrastructure (Barnett et al., 2005; Milly et al., 2008). This study supports the results of previous research, namely that climate warming has and will continue to reduce snow accumulation (Harpold et al., 2012; Mote et al., 2018), produce earlier snowmelt onset (Regonda et al., 2005; Stewart, 2009; Clow, 2010), and reduce snowmelt rates (Musselman et al., 2017a). In addition to those key changes, the fact that the alpine and subalpine snowpacks responded differently to simulated warming brings up two further considerations. One, snow accumulation decreased at a greater relative rate in the subalpine compared to the alpine. Thus, streamflow forecasts that rely on statistical relationships between snow accumulation at a point and streamflow volume will likely degrade as the amount of snow monitored at a single station becomes progressively less and less representative of the snow accumulation in the elevations above it. This is further compounded by the fact that the SNOTEL stations used to monitor water resources have limited spatial representativeness (Meromy et al., 2013) and most are located in the subalpine, which we have shown to be more sensitive to warming than the alpine. Two, the temporal gap in snowmelt onset between the two sites increased with warming. In the baseline, subalpine peak SWE occurred an average of 21 days before alpine peak SWE. In the +4.0°C perturbation, this temporal gap expanded to 35 d, representing a relative increase of 66.7%. Compounding the problem is that a significantly larger proportion of subalpine meltwater was produced before peak SWE in the warming scenarios. Thus, reservoir operations will likely have to be updated as more meltwater is delivered earlier in the season and as spatial patterns of snowmelt onset change with continued warming.

Assumptions and Shortcomings

For this research, we based our findings on output from the SNOWPACK model. Although it has been well validated in previous studies (Lehning et al., 2001; Schmucki et al., 2014; Jennings et al., 2018a), using a single model has its limitations. For example, previous intercomparison studies show that model performance varies across years and sites (Etchevers et al., 2004; Rutter et al., 2009; Krinner et al., 2018). Representation of surface energy fluxes and the resultant snowmelt is dependent on model structure and parameterization of the snowpack energy balance (Etchevers et al., 2004; Marks et al., 2008; Essery et al., 2013). Similarly, the number of modeled snowpack layers affects simulated cold content, runoff processes, and energy fluxes (Essery et al., 2013; Raleigh et al., 2016), while the partitioning of precipitation into rain and snow based on meteorological quantities leads to modeled SWE divergence (Harder and Pomeroy, 2014; Jennings and Molotch, 2019). The conclusions of any model-based study are therefore linked to the uncertainty of simulated snowpack processes.

By using the delta-change approach in this work, we assumed that future increases to air temperature would be uniform in space and time, and that the diurnal temperature range would be unaffected. However, past work has shown that snowpacks across an elevational gradient are sensitive to the diurnal temperature range (Nayak et al., 2010) and that warming is associated with a decrease in the diurnal temperature range (Karl et al., 1991). Therefore, we are likely missing changes to snow cover evolution induced by variations in the diurnal temperature range. Such changes may include a decrease in nighttime cooling of the snowpack and reduced refreezing of liquid water, meaning daytime positive energy fluxes could go toward melting the snowpack instead of warming it. We also assumed air temperature changes would be equivalent at the two sites despite previous research in the Rocky Mountains showing such trends are dependent on elevation (Williams et al., 1996; Pepin and Losleben, 2002; McGuire et al., 2012). However, it should be noted that past studies using SNOTEL measurements may be affected by inhomogeneities in the temperature data (Oyler et al., 2015).

Additionally, we did not consider changes to precipitation in this work due to the high interannual variability and uncertainty in future projections (IPCC, 2013; Easterling et al., 2017) and because our research focuses on the sensitivity to near-certain warming. Previous work over large spatial scales suggests that increases in precipitation would have to be substantial in order to make up for the effect of future warming air temperatures on snowpack accumulation (Adam et al., 2009; Marty et al., 2017) and streamflow (Barnett and Pierce, 2009; Udall and Overpeck, 2017). In the context of the results presented herein, winter snowfall would have to increase by at least 43.9 mm in the alpine and 54.3 mm (liquid equivalent) in the subalpine (Table 2) to account for the predicted loss in peak SWE for every 1°C of warming. However, this is likely a significant underestimate as future increases in winter snowfall caused by higher precipitation would be counteracted by predicted changes in melt timing and magnitude (e.g., Rasouli et al., 2014, 2015). Similarly, decreases in precipitation would compound the warming effects, leading to pronounced warm and dry snow droughts (Harpold et al., 2017a)

For this paper we only examined two point locations and did not consider the broader spatial extent of the Niwot Ridge LTER and the associated variability in snowpack accumulation and melt (Jepsen et al., 2012). Previous research has shown that point observations of SWE are limited in their representativeness of the surrounding landscape (Molotch and Bales, 2005, 2006) and that meltwater outflow and timing can vary over short distances (Webb et al., 2018a,b). This is due to both variability in snowpack internal properties and the spatial variation of the snowpack energy budget (Marks and Winstral, 2001; Pomeroy et al., 2003; Dadic et al., 2013). Thus, there is evidence to suggest that proximate snowpacks experiencing the same changes in climate would respond differently due to variations in physiography (e.g., Tennant et al., 2017). Additionally, our work focused on only two cold continental sites, but there remains a large diversity of seasonal snow cover classes in the western United States (Armstrong and Armstrong, 1987; Serreze et al., 1999; Trujillo and Molotch, 2014). We chose these locations because of their long-term meteorological and snow pit records and because they could represent sites that past work has shown to be more (the subalpine) and less (the alpine) sensitive to the impacts of climate change on snow accumulation and melt. Although this research cannot be transferred directly to other areas, we believe our findings can be used to inform future research. Continuing to explore the differential response of alpine and subalpine snowpacks to warming will be critical considering that elevations above 3,000 m in the Colorado River Basin provide ~50% of streamflow to the river (Hammond et al., 2018).

Other Factors Driving Changes to Snow Accumulation and Melt

Landscape-scale disturbances to forested areas, such as wildfire and bark beetle infestation produce marked impacts on mountain snowpacks (Gleason et al., 2013; Livneh et al., 2015). Light absorbing particles, such as dust, also have a pronounced effect on snowmelt timing and streamflow generation (Skiles et al., 2012; Painter et al., 2017). Both dust and post-wildfire char decrease surface albedo, which increases Q_SW and contributes to greater Q_M values (Painter et al., 2010, 2012; Deems et al., 2013; Gleason and Nolin, 2016). Therefore, research on the future of snow in the western United States should consider the effects of landscape disturbances and light absorbing particles on snow accumulation and melt as they may exacerbate the warming response, particularly if feedbacks between snow and forest regeneration are considered (Knowles et al., 2017). Additionally, light absorbing particles will likely have spatially varying impacts as albedo reductions due to wildfire char in the subalpine can be temporally persistent (Gleason et al., 2019), while dust is a more seasonal phenomenon in the alpine (Painter et al., 2012). For this study, we focused only on changes in climate given the high certainty in future air temperature increases (IPCC, 2013).

Furthermore, Harpold and Brooks (2018) reported that relative humidity can help explain the differential inter-regional response to climate warming. Their analysis of 462 SNOTEL stations indicated that sites with lower relative humidity saw a reduced impact of increased air temperatures on snowpack ablation relative to sites with higher relative humidity. They note that drier sites, like the ones studied here, are buffered against the effects of climate warming through energy losses from Q_LW and Q_LE. While their study explains the large-scale controls on the non-linear response of snowpacks to climate warming, our work shows there can still be significant differences over short distances at sites with similar seasonal relative humidity values.

Conclusion

The snowpacks at the two sites evaluated in this study displayed a differential response to simulated climate warming. For every 1°C of warming, peak snow water equivalent declined by 43.9 mm in the alpine and 54.3 mm in the subalpine, melt onset shifted earlier by 6.2 days in the alpine and 8.8 days in the subalpine, the snow season became shorter by 10.7 days in the alpine and 16.4 days in the subalpine, and melt rate increased by 0.2 mm d⁻¹ in the alpine while decreasing by 0.4 mm d⁻¹ in the subalpine. We found this differential response was primarily the result of the interplay between snowfall fraction, cold content, and the snowpack energy balance. In our study, subalpine snowfall fraction declined at more than twice the rate of alpine snowfall fraction, causing greater reductions in incoming frozen mass. This combined with warmer air temperatures led to peak subalpine cold content approaching 0 MJ m⁻², while alpine cold content was still large enough to buffer against mid-winter melt events caused by increased positive energy fluxes. At 3°C of warming and greater, the subalpine site experienced a tipping point where significant melt could occur throughout the entirety of the winter. This finding has implications for the timing and magnitude of meltwater delivery from the vast subalpine area of the seasonal snow zone as warming-induced reductions to snowfall fraction and cold content plus changes to the snowpack energy balance continue in the years ahead.

Data Availability Statement

The meteorological data (Jennings et al., 2017, 2018a) used to force the SNOWPACK model are available through the LTER network: https://doi.org/10.6073/pasta/1538ccf520d89c7a11c2c489d973b232. The SNOWPACK configuration files can be accessed online: http://dx.doi.org/10.17632/gxpzfycs5r.1. The snow pit validation data (Williams, 2016) are also freely available through the LTER network: https://doi.org/10.6073/pasta/2148e1a33390fc0a4ecc5226c5ccc31a. SNOTEL data can be accessed from the National Resources Conservation Service: https://www.wcc.nrcs.usda.gov/snow/.

Author Contributions

KJ and NM designed the study. KJ performed the modeling and analysis, and wrote the manuscript. NM edited the manuscript.

Funding

Funding for KJ was provided by a NASA Earth and Space Science Fellowship (16-EARTH16F-378). Additional project funding was provided by NASA grants 80NSSC17K0071 and NNX17AF50G. The Niwot Ridge LTER was funded by the United States National Science Foundation (NSF DEB #1637686).

Conflict of Interest

KJ is employed by Lynker.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the three reviewers and the editor, Dr. ML, for their constructive feedback.

References

Abatzoglou, J. T. (2011). Influence of the PNA on declining mountain snowpack in the western United States. Int. J. Climatol. 31, 1135–1142. doi: 10.1002/joc.2137