How Much Water in Basaltic Melts Parental to Porphyry Copper Deposits?

Porphyry copper deposits are formed by aqueous fluids exsolved by differentiated, mantle-derived magmas variably mixed with crustal melts. Water is essential to form porphyry Cu mineralization, and this explains why these deposits are found only at convergent margin settings, where subduction has enriched the mantle source of magmas with slab-derived H₂O. Intuitively, the more water occurs in the parental magmas of porphyry deposits, the more fertile the latter should be. Indeed, several studies have proposed that anomalously high H₂O contents in the source basalt, resulting, for instance, from subduction of large-scale serpentinized fracture zones of the oceanic slab, could increase the fertility of magmas. However, no studies have ever quantified the effects of variable H₂O contents on the fertility of parental basalts to form porphyry deposits. Here, using petrological modeling with a Monte Carlo approach, I show that the optimum amount of slab-derived H₂O in fertile parental basalts is ∼2–6 wt%, which coincides with the measured range of H₂O content in arc basalts. Lower and higher amounts of H₂O in the parental basalt lead to less porphyry-fertile magmas. The lower fertility of H₂O-poor parent basalt (i.e., <2 wt%) predicted by the model is understandable as the result of an overall lower amount of fluid that can be exsolved by the magmatic system once it reaches H₂O saturation. In contrast, the decrease in the fertility of H₂O-rich parental basalts (>6 wt%) predicted by the model is counterintuitive. The reason for the decreased fertility of parental basalts with >6 wt% H₂O is that such H₂O-rich magmas undergo fluid saturation, losing their fluid and metal cargo at deep crustal levels. Additionally, water saturation-induced crystallization of amphibole at these deep levels prevents such H₂O-rich magmas from ascending to shallower crustal levels, where they can form porphyry deposits. The conclusion that arc basalts with normal H₂O contents (∼2–6 wt%) are the most porphyry-fertile adds evidence to the hypothesis that intermediate-felsic magmas associated with porphyry Cu deposits are parented by arc basalts formed through normal subduction-related processes and that intracrustal and tectonic processes play the most relevant role in the modulation of Cu endowments of these deposits.

Introduction

Water is one of the essential ingredients to make porphyry copper deposits, together with Cu, Cu ligands (e.g., Cl^– and HS^–), and sulfur combining with Cu to form ore minerals (Burnham, 1979; Richards, 2011; Seward et al., 2014; Chiaradia and Caricchi, 2017). A large body of literature has shown that the origin of the greatest majority of the water, Cu, and ligands in porphyry-type deposits is magmatic (e.g., Burnham, 1979; Cline and Bodnar, 1991; Hedenquist and Lowenstern, 1994; Heinrich et al., 2005). Because Cu, ligands, and S have finite solubility in their carrying agent (H₂O), the amount of water available to form a deposit is one of the main controls of the maximum metal endowment of a porphyry copper deposit (Chiaradia and Caricchi, 2017). The amount of available water, in turn, depends on the volume, composition, and pressure conditions of the silicate melt into which such water is initially dissolved (Chiaradia and Caricchi, 2017).

Porphyry copper deposits are typically associated with intermediate to felsic magmas with calc-alkaline to variably alkaline affinity in convergent margin settings (e.g., Richards, 2009; Sillitoe, 2010; Chiaradia, 2020). In this geodynamic context, porphyry copper deposits occur in both syn-subduction (typical Andean- or Cordilleran-type porphyry deposits) and post-subduction (syn- or post-collisional, extensional) settings (Richards, 2009; Chiaradia, 2020). In both situations, primary basaltic melts, from which intermediate-felsic magmas associated with porphyry copper deposits derive, are considered to form by partial melting of a mantle metasomatized by H₂O-rich fluids (supercritical or melts) of the subducted slab. Such slab-derived metasomatism can be either coeval with the magma generation process (which may then result in syn-subduction, Andean-type porphyries) or prior to the formation of magmas (which may result in post-subduction porphyries). Although the modalities of the melting of the metasomatized mantle may change in these two geodynamic settings (e.g., mostly flux melting of asthenospheric mantle in the syn-subduction case and influx of hot asthenosphere inducing partial melting of metasomatized lithospheric mantle in the case of post-subduction; Richards, 2009), the ultimate source of water in the primary basaltic melts formed in both situations above is the slab-derived H₂O.

It is reasonable, therefore, to infer that the more slab-derived H₂O there will be in the parental basalts, the more these can be considered fertile to form porphyry-type deposits. Indeed, the formation of porphyry-type deposits has been associated with anomalous water and metal fluxes from the dehydrating subducting slab, such as, for instance, from large-scale subducted fracture zones, such as the Mocha, Valdivia, and Grijalva fracture zones currently subducting off the coasts of Chile and Ecuador (e.g., Hollings et al., 2005; Rosenbaum et al., 2005; Richards and Holm, 2013). These fracture zones are more intensely serpentinized than average oceanic crust and therefore, during subduction, could liberate higher amounts of slab-derived H₂O, resulting in higher H₂O contents in the primary basaltic melts (Rodríguez et al., 2007). Additionally, the crustal thickness of the overriding plate is believed to control the depth at which mantle melting occurs (Turner and Langmuir, 2015; Perrin et al., 2018), which in turn may also modulate the water content of arc magmas (Turner et al., 2016; Chin et al., 2018). Arcs with thinner crust are thus predicted to be associated with primary basalts having lower water contents as compared with primary basalts generated under arcs emplaced onto thicker crust (Turner et al., 2016; Chin et al., 2018). Under this point of view, it might be worth investigating whether there is a link between this potential H₂O enrichment in primary basalts associated with thick arcs and the observation that the largest porphyry Cu deposits are usually formed in arcs with very thick overriding plate crust (e.g., Central Andes).

On the other hand, porphyry Cu deposits are associated with intermediate-felsic magmas, which will inevitably upgrade the initial H₂O content of the parent primary basalt, because H₂O behaves as an incompatible element during magma differentiation. Therefore, the ultimate amount of H₂O available in the magmas of intermediate-felsic compositions typically associated with porphyry Cu deposits will be controlled by the initial slab-derived H₂O content of the parent melt, the degree and depth of its evolution, and, eventually, the amount of H₂O provided by assimilated or partially melted lithologies at different crustal levels.

Here, I test through petrologic modeling the roles played by each one of the above H₂O potential sources and upgrading mechanisms in order to define the optimal slab-derived H₂O contents in the parental melt to generate H₂O-fertile magmas for porphyry copper deposits. The conclusions of this study may help in understanding whether or not geodynamic and petrologic source processes leading to anomalous H₂O enrichment in primary basalts parental to porphyry copper systems are a necessary step in the formation of such type of deposits.

Materials and Methods

Petrologic Modeling Background

The aim of this study is to provide, through petrologic modeling, constraints on the optimal H₂O contents of primary arc basalts that are parental to intermediate-felsic magmas associated with porphyry copper deposits. Several studies have postulated the importance of large-scale oceanic fracture zones as feeders of increased H₂O contents into the mantle wedge, which could result in anomalously H₂O-rich basalts (Rodríguez et al., 2007), as the parents of magmas associated with porphyry copper deposits (e.g., Hollings et al., 2005; Rosenbaum et al., 2005; Richards and Holm, 2013). However, such a question has never been addressed from a quantitative point of view. Chiaradia and Caricchi (2017) have carried out petrologic modeling of intracrustal magmatic systems parented by basalts with H₂O contents (2–4 wt%), which can be considered as “normal,” according to results of Plank et al. (2013) that arc basalts contain 2–6 wt% H₂O with an average of ∼4 wt%. Here, I model what are the effects of changing the H₂O contents of the primary parental basalts over a wider range of values (0.1–12 wt%) on their fertility to form porphyry copper deposits.

Modeling is sub-divided into two parts because the H₂O enrichment in the primary basalt is only the first step in generating H₂O-fertile magmatic systems in arcs. The second step is the upgrading of the initial H₂O content of the primary basalt that occurs through intracrustal evolution (e.g., fractional crystallization, mixing, and partial melting; see below) of the parent basalt. The first part (section “H₂O Contents in Primitive Mantle-Derived Basalts”) models the permissible range of H₂O contents of primary arc basalts. The latter are directly controlled by the H₂O concentration in the mantle wedge, mantle-melt partition coefficient of water, mantle melt fraction, and temperature and pressure at which mantle melting occurs (Kelley et al., 2010). I have linked pressure and temperature together using the mantle wedge thermal model of Perrin et al. (2018) in order to provide a more robust control of the water content of arc basalts based on a realistic mantle wedge thermal structure in a subduction zone environment.

The second part (section “H₂O and Cu Amounts Exsolvable by Derivative Magmas”) models the amount of H₂O that can be accumulated and later exsolved by magmatic systems during intracrustal evolution of primary basalts having a representative range of the initial H₂O contents obtained in the first part of the modeling. Intracrustal evolution of the basalts is carried out using the thermodynamic parameters and average arc magma flux value of the hot zone model of Annen et al. (2006), as detailed below. Because this part of the model is based on thermodynamic parameters and magma fluxes that are typical of syn-subduction zones, the overall model here presented and discussed applies to syn-subduction porphyry copper deposits. The lack of magma flux data in the post-subduction environment hinders, for the time being, extension of the model to post-subduction porphyry copper deposits.

I would like to highlight that, as for every model, this one is also aimed at providing first-order general constraints and that exceptions are obviously possible and likely for individual specific situations.

H₂O Contents in Primitive Mantle-Derived Basalts

The H₂O contents of basaltic partial melts of mantle peridotite have been calculated using Eq. 4 of Kelley et al. (2010)

$C_{{\text{H}}_2\text{O}}^0=\left[D_{{\text{H}}_2\text{O}}\left(1-F\right)+F\right]\times {\left[{\displaystyle \frac{T-\left(a{P}^2+bP+c\right)-\left(x\ln \left(P\right)+y\right)F}{-60}}\right]}^{1.85}(1)$

where ${\text{C}}_{{\text{H}}_2\text{O}}^0$ is the H₂O concentration in the mantle wedge, D_{H_2 O} is the mantle-melt partition coefficient of water (allowed to range randomly between 0.006 and 0.01, a typical range of values according to Plank et al., 2013; Table 1), F is the mantle melt fraction (allowed to range randomly between 0.05 and 0.25, typical values of mantle wedge melting according to Plank et al., 2013; Table 1), T is temperature in°C, P is the pressure in GPa, and a, b, c, x, and y are constants with values of −5.1404654, 132.899012, 1120.66061, −221.34, and 536.86, respectively (Supplementary Data Sheets S1, S3). This equation, which is a re-formulation of the equation of Langmuir et al. (2006), considers the combined effects of pressure and temperature on the partial melting of the mantle. Eq. 1 shows a dependence of ${\text{C}}_{{\text{H}}_2\text{O}}^0$ on the P and T conditions of the mantle wedge. In order to get a realistic control by these parameters on ${\text{C}}_{{\text{H}}_2\text{O}}^0$, I have linked P and T together using the mantle wedge thermal model of Perrin et al. (2018) (Supplementary Figure S1 in Supplementary Data Sheet S3). According to this model, the thermal structure of the mantle wedge changes systematically with increasing thickness of the crust of the overriding plate.

TABLE 1

Table 1. Values used for input parameters in the model of mantle melting.

H₂O and Cu Amounts Exsolvable by Derivative Magmas

Modeling of the H₂O and associated Cu exsolvable by magmas derivative of primary basalts is carried out through a set of equations written in Excel (Supplementary Data Sheets S2, S3) to quantify, using a Monte Carlo approach (Table 2), the following main parameters: (i) the amounts of hybrid melt produced in the crust (melt productivity indicates the amount of hybrid melt accumulated divided by the amount of total intruded basaltic melt) through processes typical of hot zones as discussed in the main text (Annen et al., 2006), (ii) their water contents (in solution, in excess, and exsolvable at the pressure of saturation), and (iii) the Cu contents in the exsolvable water at the pressure of saturation and the SiO₂ composition of the hybrid melts produced within the crust. In the specific case, several thousands of Monte Carlo simulations were used to obtain the model results discussed in the text. Below I discuss in detail how the three main parameters above (i, ii, and iii) have been quantified in the model.

TABLE 2

Table 2. Values used for input parameters in the intracrustal evolution model.

Melt Productivity

Melt productivity is quantified at different crustal depths using the model of Annen et al. (2006), as implemented by Chiaradia and Caricchi (2017) and Chiaradia (2020). In this model, basaltic magma is injected at a temperature of 1,285°C into the arc crust at a fixed average rate of 0.0009 km³/a, corresponding to a typical arc long-term average rate. Injection is allowed to occur at different crustal levels (from ∼5 km = 0.15 GPa to ∼30 km = 0.9 GPa) for time intervals up to 5 Ma (Table 2). The range of crustal depths (5–30 km) at which injection occurs corresponds to a typical range of mid to lower crustal thicknesses in continental arcs (Annen et al., 2006) and the duration of several Ma of injection is consistent with the evidence of more or less continuous multi-Ma magmatism (up to >5 Ma) occurring in several porphyry systems prior to the onset of mineralization (e.g., Chiaradia et al., 2009; Stern et al., 2010; Chelle-Michou et al., 2014). Continuous injection of mantle-derived basaltic melts results in cooling and fractionation of the basaltic melt and concomitant heating of the surrounding rocks (the thermodynamic parameters used in the model, such as density, specific heat capacity, specific latent heat, and thermal conductivity are those reported in Table 1 of Annen et al., 2006). Initially, cooling will continue until the solidus of the fractionating basalt is reached, but, after a certain time, due to continuous heating, the surrounding rocks will reach a temperature above the solidus of the lowest temperature derivative melt from the fractionating basalt. This means that some derivative melt (initially with the lowest possible solidus temperature, i.e., rhyolitic in composition) will no longer solidify. Due to continuous injection of basaltic melt from the mantle, this residual melt will mix with new coming basalt, producing a hybrid melt with intermediate composition. All this process will result in a growing mass of melt through time that is a hybrid result of the mixing of derivative melt from fractionating basalt, new coming basalt, and partial melt of the host rocks. This process is increasingly efficient at deeper crustal levels because host rocks are hotter at deeper injection levels (the model of Annen et al., 2006 uses a geothermal gradient of 20°C/km).

The curves of melt productivity have been parameterized from Annen et al. (2006) for both residual (M_residual) and crustal melt (M_crustal) fractions (Supplementary Figure S2 in Supplementary Data Sheet S3). The detailed equations of the parameterization of the residual and crustal melt fractions are reported in the caption of Supplementary Figure S2 in Supplementary Data Sheet S3.

H₂O Concentrations in the Hybrid Melt

Melt productivity as determined above was coupled to H₂O concentrations in the hybrid melt assuming slab-derived H₂O contents of 0.1, 1, 2, 4, 6, 8, and 12 wt% in the mantle-derived basalt (Figures 1, 2) and a range between 0.2 and 1.0 wt% H₂O in the amphibolitic (lower) to graywacke (upper) crust of the Annen et al. (2006) model (Table 2). A completely incompatible behavior of H₂O during the hybrid melt accumulation process was assumed. The chosen range of slab-derived H₂O contents in the mantle-derived basalts (0.1–12 wt%) is representative of the possible primary arc basalt H₂O contents obtained through modeling (Figures 1, 2), whereas the H₂O content range of the crust corresponds to typical contents of hydrous minerals in crustal lithologies (for instance, a 1.0 wt% content of amphibolitic crust corresponds to an amphibolite with 50% modal amphibole having a nominal H₂O content of 2 wt%). VolatileCalc (Newman and Lowenstern, 2002) was used to calculate water solubility in melts according to the pressure of accumulation and hybrid melt composition (Supplementary Figures S3–S5 in Supplementary Data Sheet S3). In order to take into account the effects of different pressures of accumulation on the results, simulations were carried out for narrow ranges of pressures corresponding to ∼0.4 (range 0.38–0.40), ∼0.6 (range 0.58–0.60), and ∼0.8 (range 0.78–0.80) GPa. These are representative pressures of magma evolution in transcrustal magmatic systems (e.g., Annen et al., 2006; Cashman et al., 2017). This way, the H₂O contents of the melts and the degree of H₂O over- or undersaturation in the hybrid melts produced at these different crustal levels (pressures) and for different durations of injection could be determined. This allowed the determination of the amount of exsolvable H₂O (i.e., dissolved in undersaturated magmas) and exsolved H₂O (i.e., for H₂O-saturated systems) associated with any specific hybrid melt produced after any injection time, at the crustal depths corresponding to ∼0.4, ∼0.6, and ∼0.8 GPa, for the different initial H₂O contents above in the parent basalt.

FIGURE 1

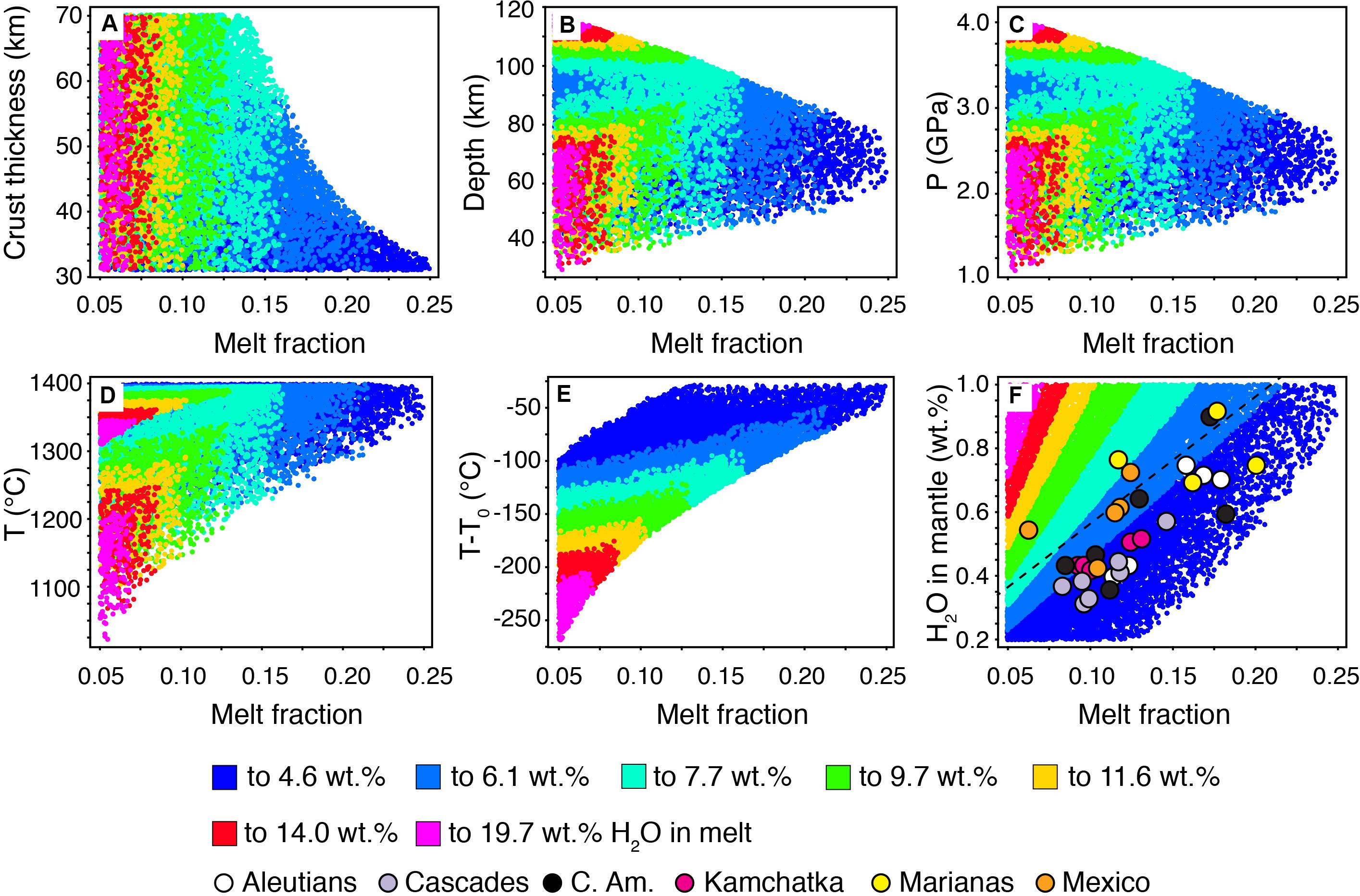
Figure 1. Monte Carlo simulations of the dependency of mantle melt fractions in primary basalts on various parameters. Monte Carlo simulations (>15,000) of the dependency of mantle melt fractions with respect to overriding crust thickness (A), depth of melting (B), P of melting (C), T of the mantle wedge (D), T–T₀ (E), and H₂O content in the mantle wedge (0.2–1.0 wt% interval) (F). Color codes highlight the different intervals of H₂O contents in the associated, mantle-derived, primary basalts. The mantle melt fraction is mostly controlled by thickness of the overriding plate (A), T of the mantle wedge (D), T–T₀ (E), and H₂O content of the mantle wedge (F). The data plotted in panel (D) are from Plank et al. (2013). C. Am. = Central America.

FIGURE 2

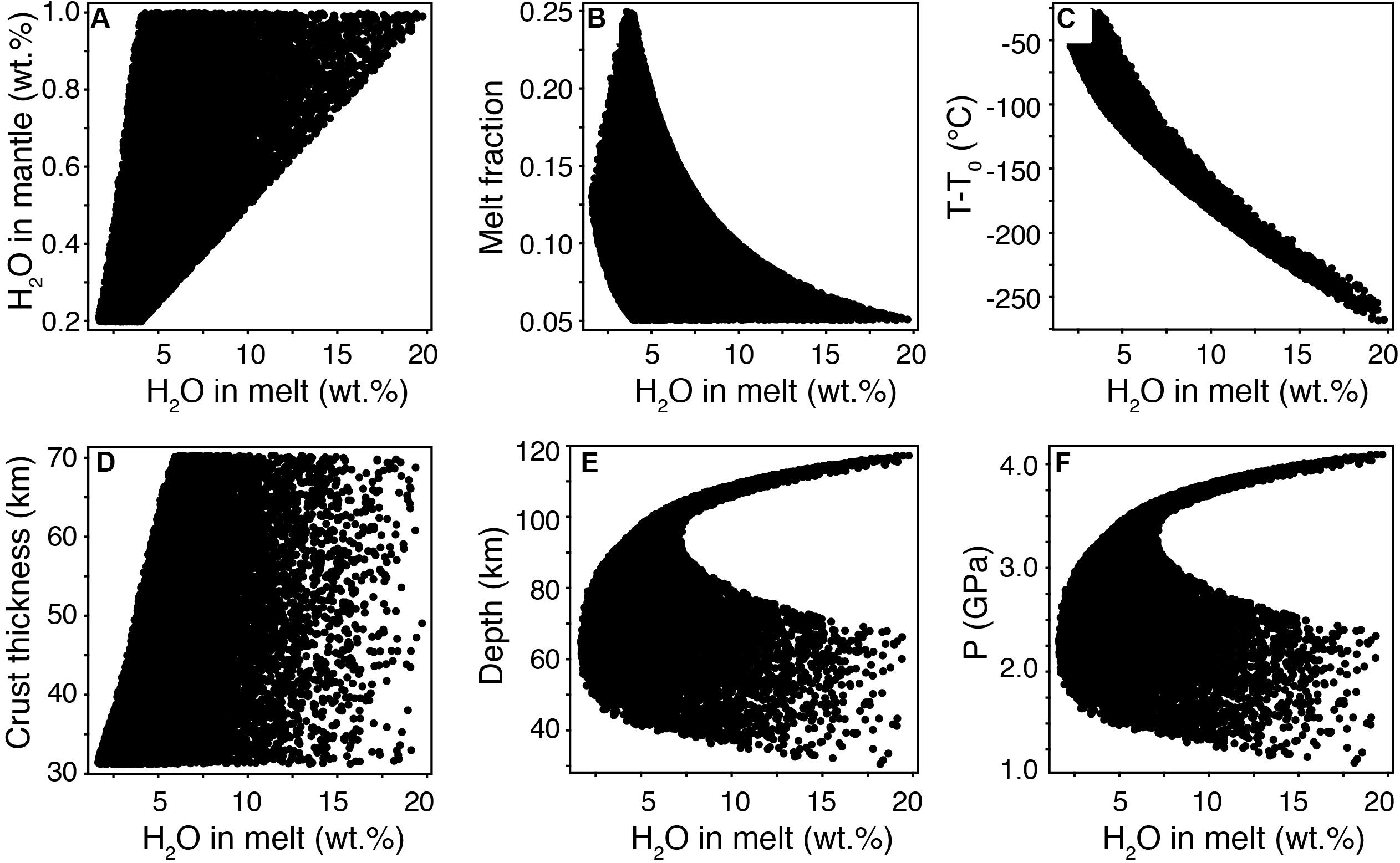
Figure 2. Monte Carlo simulations of the dependency of H₂O contents in primary basalts on various parameters. Monte Carlo simulations (>15,000) of the dependency of H₂O contents in primary basalts with respect to H₂O content in the mantle wedge (0.2–1.0 wt% interval) (A), melt fraction (B), T–T₀ (C), overriding crust thickness (D), depth of melting (E), and P of melting (F). H₂O contents in primary basalts display variable correlations with H₂O content of the mantle wedge (A), mantle melt fraction (B), and T–T₀ (C), whereas they display less clear relationships with thickness of the overriding plate (D) and depth (E,F).

Hybrid Melt SiO₂ Content

In order to link the melt productivity of the model of Annen et al. (2006) to the SiO₂ content, I used the relationship below (see also Supplementary Table S1 in Supplementary Data Sheet S3) between melt fraction (M) and SiO₂ (in wt%), based on the mid-values of SiO₂ for the fields of basalt, basaltic andesite, andesite, dacite, and rhyolite of the total alkali-silica diagram (Le Bas et al., 1986) and the mid-values of the melt fraction and the corresponding composition attributed by Annen et al. (2006) (e.g., Figure 8 of Annen et al., 2006).

In a bivariate plot, the two variables above are linked through the equation

${\text{SiO}}_2=35.43629M^2-68.8591M+82.43897(2)$

The modeled SiO₂ composition is used to determine the Cu contents in the modeled melts, as explained below.

Amounts of Cu in the Exsolvable Fluid

The amounts of Cu in the exsolvable fluid depend on the concentration of Cu in such a fluid. The latter depends on the Cu concentration in the melt and on the value of the fluid-melt partition coefficient, which determines how much Cu goes into the exsolvable fluid once the latter separates from the melt. For Cu concentrations in the hybrid melt, the SiO₂-dependent Cu concentrations of continental arc magmas of Chiaradia (2014) were used. The SiO₂-Cu relationship is best fitted by a second-order equation.

$\text{Cu}=0.0632{\text{SiO}}_2-10.118{\text{SiO}}_2+407.63(3)$

where Cu is in ppm and SiO₂ in wt%. This equation expresses the covariation between median Cu and SiO₂ values from thick arc magmas (>30 km) (Supplementary Figure S6). Since there is some scatter in the SiO₂-Cu relationship (Supplementary Figure S6), all possible values within the upper and lower boundaries of this scatter have been considered and implemented in the Monte Carlo modeling. A conservative random variation of Cu fluid-melt K_D values between 2 and 100 (Chiaradia and Caricchi, 2017; Table 2) was used for all types of hybrid melt produced to calculate the amount of Cu that partitions into the fluid phase exsolved or exsolvable from the melt.

Plotted Data

The data obtained from the intracrustal modeling and plotted in Figure 3 are median values of various parameters obtained from Monte Carlo simulations (i.e., exsolvable Cu, hybrid melt volume, exsolvable H₂O, and exsolved Cu) for basalts with variable slab-derived H₂O contents (slab-derived H₂O in melt, wt%). Exsolvable Cu and H₂O are the Cu and H₂O amounts that can be potentially exsolved from the melts but have not been exsolved because melts produced in the simulations are H₂O-undersaturated. Exsolved Cu is the Cu amount that has been exsolved by H₂O-saturated magmatic systems throughout the periods of their accumulation. Hybrid melt volume is the volume of the melt produced in the hot zone process described above. Median values of the above parameters (expressed by the color dots in Figure 3) are calculated from several thousands of simulations returned by the model within the chosen narrow accumulation pressure intervals (i.e., 0.38–0.40, 0.58–0.60, and 0.78–0.80 GPa) and of injection time bins of ≤1 Ma (i.e., 0.37–1 Ma with median at ∼0.75, 1–2 Ma with median at ∼1.5, 2–3 Ma with median at ∼2.5, 3–4 Ma with median at ∼3.5, and 4–5 Ma with median at ∼4.5 Ma).

FIGURE 3

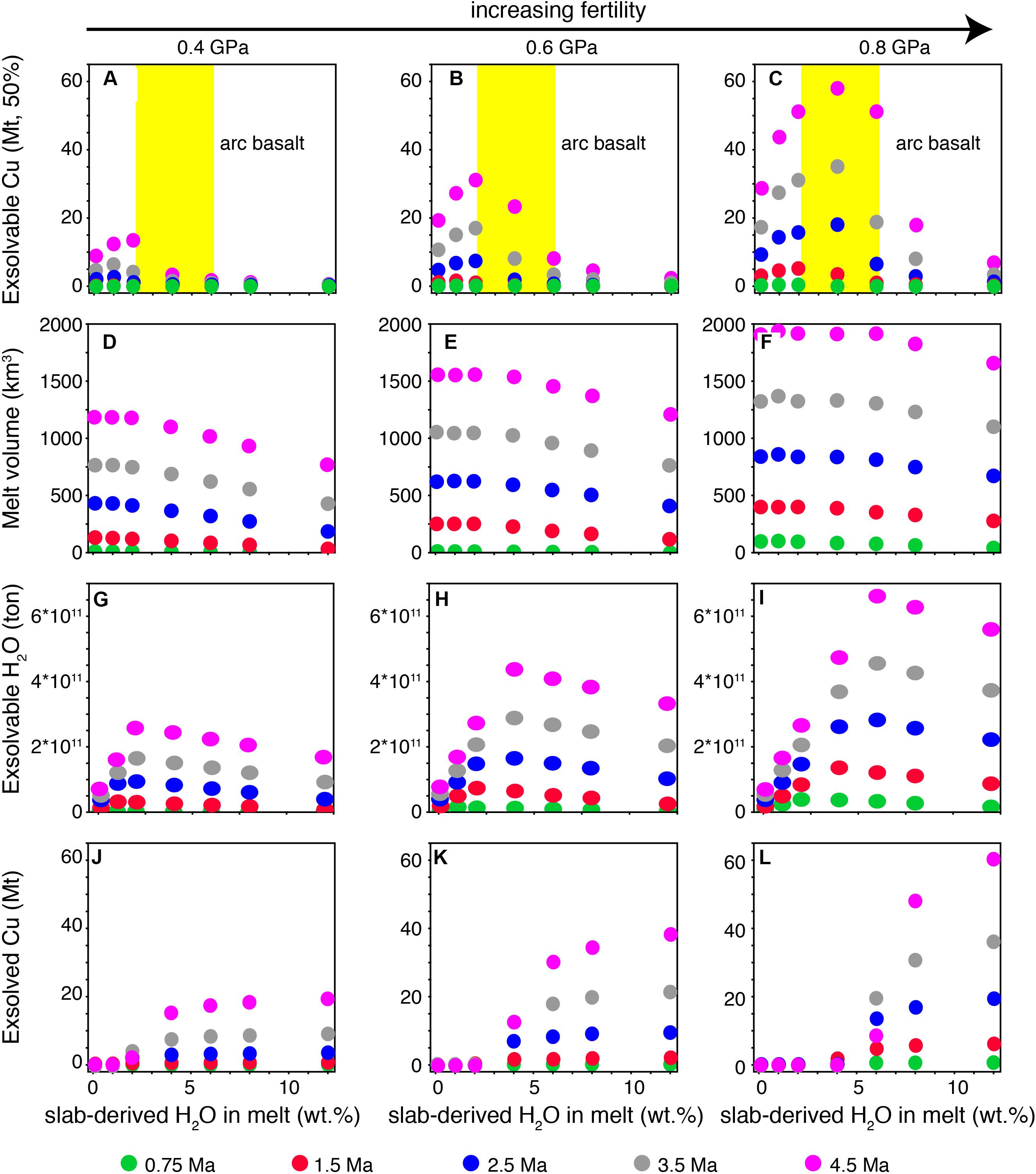
Figure 3. Variations of median values of various parameters of porphyry deposits with initial H₂O contents in parental basalts, pressure, and time intervals of magma accumulation. Median values from several thousands of simulations for exsolvable Cu (A–C), melt volume (D–F), exsolvable H₂O (G–I), and exsolved Cu (J–L) are related to three pressures at which magma accumulation may occur in magmatic arcs (0.4, 0.6, and 0.8 GPa) and to different time lengths of magma accumulation at those depths. The differently colored dots represent different accumulation times of magmas at the corresponding crustal level. Exsolvable Cu is the Cu that can be potentially exsolved from the magmas but has not been exsolved because magmas produced in the simulations are H₂O-undersaturated. Exsolved Cu is the Cu that has been exsolved by H₂O-saturated magmatic systems throughout the periods of their accumulation. This figure shows that the most fertile parental basalts are those with initial, slab-derived H₂O contents (H₂O in melt) of about 2–6 wt% (for further discussion, see the text). The yellow fields in panels (A–C) represent the range of slab-derived H₂O in arc basalts (Plank et al., 2013).

Model Limitations

The modeling concerning the determination of H₂O concentrations in primary arc basalts (Figures 1, 2) is used to obtain a realistic input range to test the effects of variable initial H₂O contents in arc basalts on their fertility toward porphyry Cu deposit formation (Figure 3). The “novelty” of this model is the coupling of the mantle H₂O content dependence on pressure and temperature (Eq. 1) with a pressure-temperature covariation constrained by a realistic thermal structure of the mantle wedge (model of Perrin et al., 2018; Supplementary Figure S1 in Supplementary Data Sheet S3). Such a model is nonetheless constrained only for a fixed slab dip of 60°. Most porphyry systems form in subduction zones with shallower subduction angles (e.g., Cooke et al., 2005), and implementation of a mantle wedge thermal structure associated with such a shallower subduction would be beneficial to a more refined model.

The intracrustal model (Figure 3), which allows the modeling of the amounts of H₂O and Cu exsolvable from intermediate-felsic magmatic systems, is based on the thermodynamic and magma flux parameters of Annen et al. (2006). Application of this model to the evaluation of Cu and Au endowments of porphyry systems as well as the Sr/Y values of the associated magmatic systems has proved to be successful as shown by the reproducibility of real porphyry data by model results of Chiaradia and Caricchi (2017) and Chiaradia (2020). I expect that the intracrustal modeling, which is the same as the one used by Chiaradia and Caricchi (2017) and Chiaradia (2020), returns results that are consistent also in this case. Unfortunately, it is not possible to test this through real data because of the rarity (or absence) of primitive magmas in most magmatic systems associated with porphyry deposits and the lack of information on the H₂O contents of such primary basalts in studies of porphyry-related magmatic systems. Focused studies on melt inclusions in mafic minerals (e.g., olivine) of magmatic systems associated with porphyry deposits should be carried out for this purpose in order to test the results of the model here presented.

Another limitation of the model here presented is that it cannot be applied to post-subduction porphyry systems for which no adequate magma flux data are currently available. Determining magma fluxes in the post-subduction environment would be necessary, adopting, for instance, the method proposed by Caricchi et al. (2014), to understand whether intracrustal magmatic processes leading to the formation of porphyry Cu deposits in such an environment are similar or not to those of the syn-subduction porphyry systems.

Results

H₂O Contents of Primary Basaltic Melts

Results of modeling of mantle melting and of H₂O contents of primary arc basalt are reported in Figures 1, 2. Due to the model constraints used here (i.e., the dependency of the thermal structure of the mantle on the thickness of the crust of the overriding plate; Perrin et al., 2018; Supplementary Figure S1 in Supplementary Data Sheet S3), increasing fractions of partial melting of the mantle wedge are associated with decreasing crust thickness, increasing T of the mantle wedge, increasing difference between the mantle wedge temperature (T) and the temperature (T₀) of the solidus of the peridotite (T–T₀), and increasing H₂O content of the mantle wedge (Figure 1).

Figure 1 shows also the dependence on the above parameters of H₂O concentrations in the basaltic melts resulting from different degrees of partial melting of the mantle. H₂O contents of the basalts can reach very high contents (>12 wt%) only for low degrees of partial melting (<7.5%) and for the largest difference between the mantle temperature (T) and the peridotite solidus (T₀) temperature (T–T₀). Figure 2 shows that the slab-derived H₂O contents of primary basalts display correlations with the initial H₂O contents of the mantle wedge (Figure 2A), melt fraction (Figure 2B), and especially T–T₀ (Figure 2C), whereas they are less clearly correlated with crust thickness (Figure 2D) and depth of melting of the mantle wedge (Figures 2E,F).

According to the model here presented, H₂O contents in primary basaltic melts can range widely between 1.5 and ∼20 wt% (Figures 1, 2). This is in contrast with the rather homogeneous H₂O contents (2–6 wt% with an average of ∼3.9 ± 0.4 wt%) measured in arc basaltic melts (Plank et al., 2013). The latter are reported in Figure 1F for comparison and show a good agreement with the results of the model here presented (i.e., the greatest majority of the measured data plot at H₂O contents between 2 and 6 wt% of the model). The homogeneous H₂O of arc basalts (Figure 1F) might suggest a more restricted range of P-T conditions under which arc primary basalts effectively form compared with the broad range here simulated, or a subsequent re-equilibration of these melts through fractionation at shallower depths (Plank et al., 2013; Turner and Langmuir, 2015). This latter point, however, seems to be at odd with extensive geochemical and thermobarometric evidence of magmatic evolution at significantly deeper crustal levels than the one needed for re-equilibration at ∼4 wt% H₂O (i.e., ∼6 km) for many arc magmas, especially in continental arcs (Foden and Green, 1992; Grove et al., 2003; Annen et al., 2006; Chiaradia, 2015; Edmonds et al., 2019).

Beyond these uncertainties, I will address below the question whether primary basaltic melts with broadly different slab-derived H₂O contents (independently of the various parameters that may control these variations; Figures 1, 2) are differently fertile in terms of amounts of H₂O deliverable to a magmatic-hydrothermal system potentially associated with a porphyry copper deposit.

Mantle or Crustal H₂O in Porphyry Deposits?

A first observation is that, according to the above model, H₂O in the hot zone intermediate-felsic magmas that ultimately feed the shallower magmatic-hydrothermal systems of porphyry copper deposits comes from the slab-derived H₂O present in the mantle-derived basalt and from crustal H₂O occurring in hydrous minerals of the crustal rocks into which the basaltic melt intrudes until it eventually partially melts them. Monte Carlo simulations of fertile magmatic systems (>5 Mt Cu at 50% efficiency, for initial H₂O contents in the primary basaltic melts of 4 wt%) show that 80–95% of the exsolvable H₂O from these magmatic systems at any time of their temporal evolution (0–5 Ma) and at any depth (5–30 km) is ultimately slab-related H₂O of the residual magma derived from fractional crystallization of the mantle-derived basaltic melt and only 5–20% is crustal H₂O from partial melting of a crustal lithology containing up to a maximum of 1 wt% H₂O (e.g., amphibolite, amphibole-bearing pyroxenite, or amphibole-bearing gabbro containing up to 50% of amphibole with a putative H₂O content of 2 wt%) (Figure 4). This shows that the slab-derived H₂O content of the primary basaltic melt is the most important portion of the H₂O ultimately forming the porphyry deposits and that crustal water (although it can be significant; Davidson et al., 2007) is subordinate in the formation of these deposits (at least considering the average magmatic arc flux used in the model). Therefore, evaluating the effect of variable H₂O contents of the primitive melts on the fertility of the derivative magma is justified.

FIGURE 4

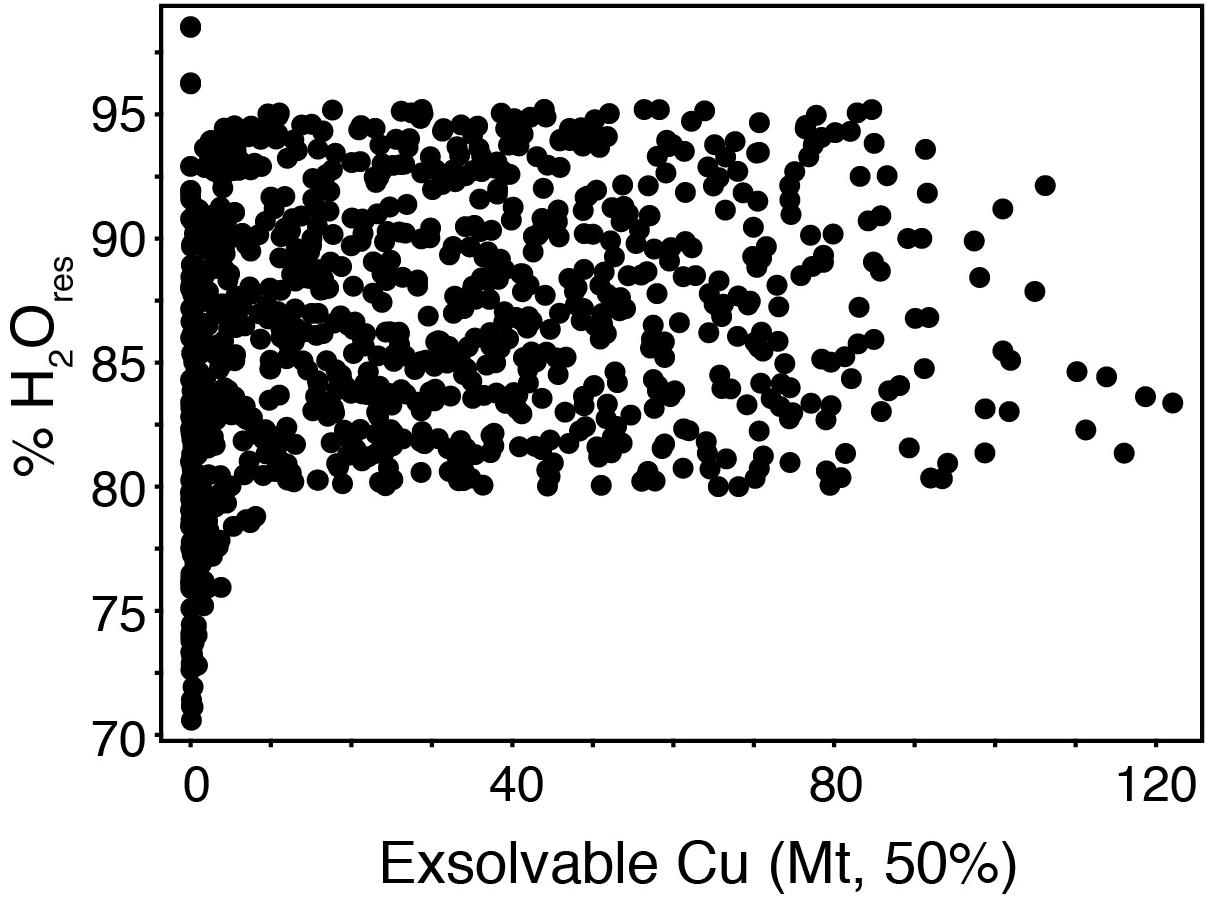
Figure 4. Monte Carlo simulations of the contributions of mantle-derived basalt H₂O to Cu-bearing fluids. Monte Carlo simulations (>1,000) of the proportions of H₂O derived from fractional crystallization of mantle-derived basalt (H₂O_res) with respect to that derived from partial melting of H₂O-bearing crustal lithologies (100%-H₂O_res). Simulations show that 80–95% of the exsolvable H₂O from porphyry-Cu fertile magmatic arc systems is H₂O of the residual magma derived from fractional crystallization of the mantle-derived basaltic melt (H₂O_res).

Chiaradia and Caricchi (2017) have shown that the most fertile magmatic systems are those formed at mid to lower crustal levels (>0.4 GPa), during long accumulation times (>2.5 Ma). Such systems contain the highest amounts of H₂O and are always H₂O-undersaturated for the range of initial H₂O (2–4 wt%) assumed in the primitive melts by Chiaradia and Caricchi (2017). Their subsequent saturation may occur only at depths shallower (12–18 km) than those of their accumulation. This means that these magmas may ascend to these shallower crustal levels from where they start to liberate fluids and metals. Figure 3 shows results for initial H₂O contents in the primary melt of 0.1, 1, 2, 4, 6, 8, and 12 wt% at three different pressures of magma accumulation (∼0.4, ∼0.6, and ∼0.8 GPa) in order to see the effects that lower and higher initial contents of H₂O in the primary basalts, with respect to those (2–4 wt%) considered by Chiaradia and Caricchi (2017), may have on the fertility of the derivative magma, typically associated with porphyry deposits. The three pressures chosen (∼0.4, ∼0.6, and ∼0.8 GPa) not only are representative of average depths of evolution in transcrustal magmatic arc systems (Annen et al., 2006; Cashman et al., 2017; see above) but also correspond to porphyry sub-fertile (∼0.4 GPa) and fertile (∼0.6 and ∼0.8 GPa) magmatic systems according to Chiaradia and Caricchi (2017). Figure 3 shows the median values of exsolvable Cu (50% efficiency), melt volume, exsolvable water, and Cu lost with fluids at variable depths (∼0.4, ∼0.6, and ∼0.8 GPa) from more than ten thousand Monte Carlo simulations run for injection time bins of ≤1 Ma (0.37–1, 1–2, 2–3, 3–4, and 4–5 Ma) for an overall magma injection period of ∼0.37 to 5 Ma. Results show that, as already discussed by Chiaradia and Caricchi (2017), the exsolvable Cu increases with increasing injection time and with injection depth (from ∼0.4 GPa sub-fertile to ∼0.6–∼0.8 GPa fertile magmatic systems; Figures 3A–C). Novel with respect to the results of Chiaradia and Caricchi (2017), they also show that at any time and depth of the ranges here considered and especially for the most fertile systems (i.e., ∼0.6 and ∼0.8 GPa), the maximum exsolvable Cu is associated with initial H₂O contents of the primary basalt between 2 and 6 wt%. For H₂O contents <2 wt% and > 6 wt%, the median exsolvable Cu decreases and falls to significantly lower values (e.g., Figure 3C).

Discussion

The decreasing fertility of the most fertile (i.e., ∼0.8 GPa) derivative magmas of basalts with low initial H₂O content (<2 wt%; Figure 3C) is intuitively understandable and is the likely reason why porphyry-type deposits occur only where primary basaltic magmas are derived from partial melting of a slab-metasomatized, hydrated mantle source. For comparison, MOR basalts contain much less initial H₂O (<0.7 wt% with a mode at 0.25 wt%; e.g., Jambon, 1994), and this content is not much upgraded through anhydrous mineral crystallization because there is limited magmatic evolution in such a geodynamic setting. The best model representation of this situation (Figure 3A) is that of the evolution of magmas at the shallowest pressure modeled (∼0.4 GPa) and for the shortest injection time (0.75 Ma). The exsolvable Cu under these conditions is virtually zero (green dots in Figure 3A).

In contrast, the decrease of the fertility of intermediate-felsic magmatic systems derived from basaltic primary magmas with high initial H₂O contents (>6 wt%; Figure 3C) is less intuitive and requires an explanation. The reason for this is that the exsolvable Cu associated with a magmatic system in the model used here is the cumulative result of the processes of fractional crystallization, partial melting, and mixing between residual melts and partial crustal melts throughout the accumulation time at different crustal levels. More fertile systems are those that can grow larger in size, in terms of both magma and H₂O amounts. Depending on the depth of formation of these magmatic systems and their evolving composition, H₂O solubility changes, and the magmatic system will reach at some stage of its evolution the optimum conditions, i.e., maximum magma volume (Figures 3D–F), but, most of all, maximum contents of exsolvable H₂O (Figures 3G–I) and thus maximum exsolvable Cu (Figures 3A–C). Conversely, magmatic systems that reach early H₂O saturation will lose Cu with the excess H₂O that is exsolving from the magma as the process of magma accumulation is still ongoing (Figures 3J–L). This strongly decreases the amount of available Cu for later exsolution at shallower crustal levels. It is unlikely that, coming from depths of several tens of km, these Cu-bearing fluids continuously exsolved during several Ma of magma accumulation are efficiently focused into a narrow rock volume at shallow depth to form an economic porphyry deposit. Additionally, geochronology data of porphyry deposits are not consistent with ore duration events of the same lengths (several Ma) as the magma accumulation periods in the continental crust (Chiaradia et al., 2013; Chiaradia and Caricchi, 2017). The fluids exsolved at depth may also remain trapped in the magma at such deep crustal levels and form Cu-bearing sulfides once sulfide saturation occurs in the magma (Chiaradia et al., 2012; Wilkinson, 2013) due to continuous magmatic evolution (Lee and Tang, 2020), thus contributing to the Cu-deficient chemistry of the continental crust (Lee et al., 2012; Chiaradia, 2014; Chen et al., 2020).

The bell-shaped curve of the exsolvable Cu versus slab-derived H₂O initial contents in the primary basalts (Figures 3A–C) indicates that there is an optimum initial H₂O content in the parental basalt that allows the magmatic systems to grow larger in size without reaching H₂O saturation with consequent loss of H₂O and Cu (Figures 3J–L). Figures 3A–C show that the peaks of exsolvable Cu in the simulations of the model are systematically lower (from ∼60 to ∼15 Mt Cu) and shift systematically to lower initial H₂O contents of the primary basalt (from 4–6 to 2 wt%) with decreasing pressure of magma accumulation. This is due to the fact that the maximum porphyry fertility of the magmatic systems is the result of optimum tuning between two parameters: (i) the enhanced fertility promoted by deeper magma evolution (corresponding to higher magma and H₂O volumes; Chiaradia and Caricchi, 2017) and (ii) H₂O contents in the primary basalt that must be not excessively high, which will promote early saturation of the melt with consequent deep loss of H₂O and Cu (Figures 3G–L), nor excessively low, which will not exploit at best the positive pressure dependency of H₂O solubility in silicate melt. The optimum H₂O content for all magmatic systems, and especially for the most fertile ones (Figures 3A–C), is between 2 and 6 wt% from the model simulations, which, interestingly, coincides with the range of H₂O contents measured in arc basaltic melts (Plank et al., 2013). If the optimum 2–6 wt% content of primary arc basalts to form fertile magmatic systems deduced by the model here presented coincides with primary arc basalts measurements (Plank et al., 2013), it remains to be clarified why modeling based on a plausible thermal structure of the mantle wedge (Perrin et al., 2018) suggests the possibility of significantly broader H₂O contents in primary arc basaltic melts (Figures 1, 2). Although the solution of this problem is beyond the scope of this investigation, a possible explanation is the fact that one of the most important parameters controlling mantle melting is the distance in the P-T space between the mantle temperature and the temperature of the peridotite solidus (T–T₀) (Langmuir et al., 2006; Portnyagin et al., 2007; Johnson et al., 2009; Ruscitto et al., 2010; Plank et al., 2013). If one considers mantle melting from the point of view of a small range of T–T₀ values as considered to happen in arcs (e.g., Plank et al., 2013), H₂O contents of the primary basaltic melts become broadly constant (for a given T-T₀ interval) and independent of the depth of the mantle melting region, temperature, mantle wedge H₂O content, and melting degree (Figure 5).

FIGURE 5

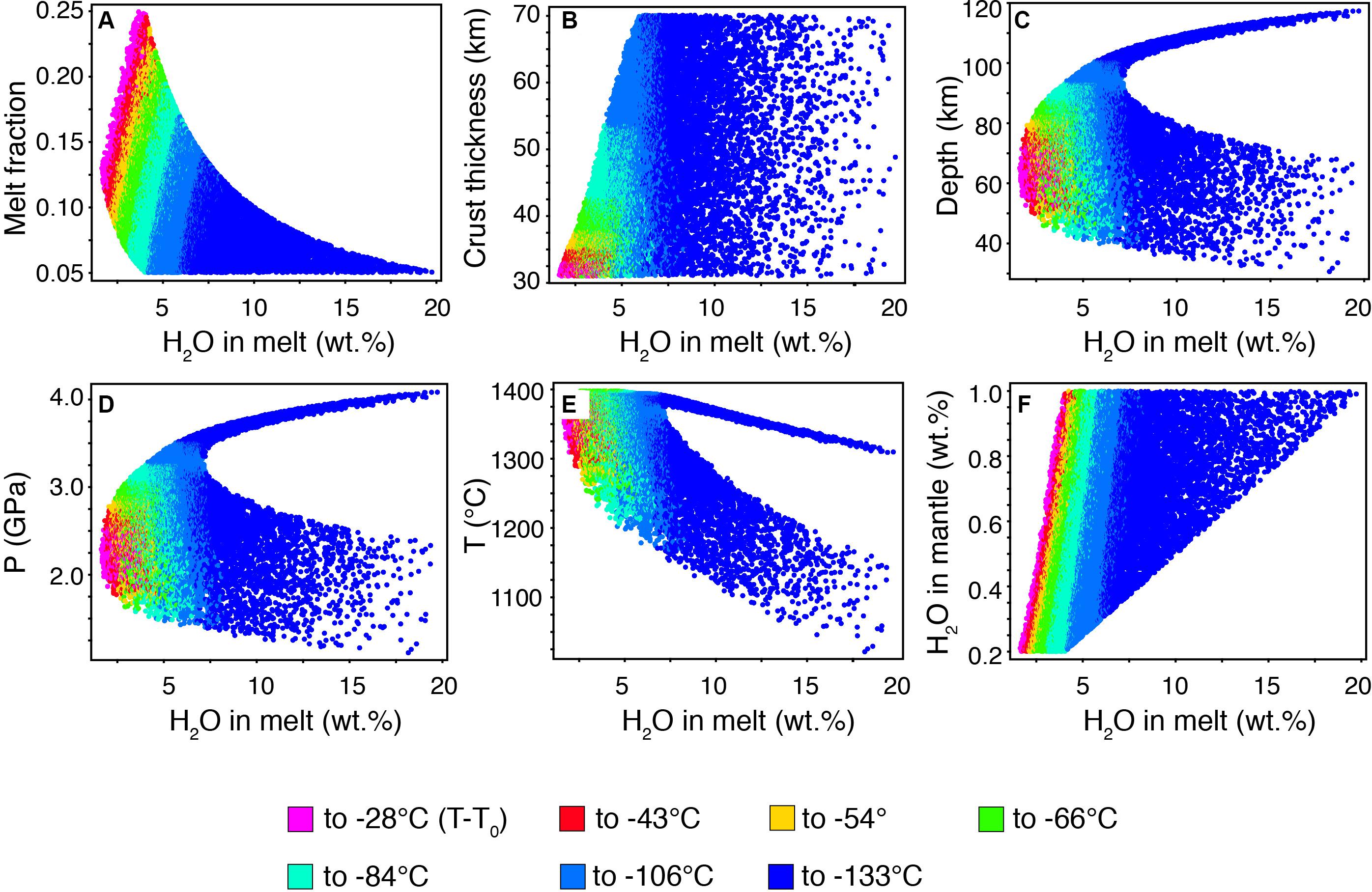
Figure 5. Monte Carlo simulations of the dependency of H₂O contents in primary basalts on various parameters. Monte Carlo simulations (>15,000) of the dependency of the H₂O contents of primary mantle-derived basalts with respect to melt fraction (A), overriding plate thickness (B), depth of melting (C), P of melting (D), T of the mantle wedge (E), and H₂O content in the mantle wedge (F). Color codes highlight the different intervals of T–T₀ values. This figure shows that H₂O contents of the primary basaltic melts are broadly constant for a given T–T₀ interval and independent of the depth of the mantle melting region, temperature, mantle wedge H₂O content, and melting degree (for further discussion, see the text).

Another factor that is not accounted for in the model but may play a negative role for very H₂O-rich primitive melts (>6 wt%) is that these melts will start to crystallize as soon as they reach H₂O saturation at deep crustal levels (e.g., Davidson et al., 2007), with their consequent “viscous death” (Barclay and Carmichael, 2004; Annen et al., 2006). In other words, these magmas will not be able to reach the shallower crustal levels from where they could eventually feed porphyry magmatic systems with the residual Cu and fluids that they still contain. This is a primary requirement for the formation of porphyry deposits as shown by geological and geophysical observations of large parental magma chambers at 10–15 km depth below the deposits (e.g., Sillitoe, 2010; Richards, 2013; Wilkinson, 2013).

The outcome of the modeling presented above is that anomalously high H₂O contents in the primary basalts (e.g., associated with higher H₂O flux of the mantle wedge or with low degrees of partial melting of the mantle wedge at deep levels) are not only not necessary for but also detrimental to the formation of the largest porphyry Cu deposits. The possibility that primary basaltic melts formed beneath thick arcs are H₂O-richer than those formed beneath thin arcs (Turner and Langmuir, 2015; Chin et al., 2018; Figure 1A) could be an appealing hypothesis to explain the occurrence of the largest porphyry Cu deposits in thick crust of the overriding plate. However, according to the model discussed above, arc basaltic magmas with normal initial H₂O contents (i.e., ∼2–6 wt%) are the most fertile to form porphyry Cu deposits, and H₂O-richer primary basalts (independently from the various potential processes causing such H₂O enrichment; Figures 1, 2) become significantly less fertile when they have H₂O contents >6 wt%. This is one additional argument in favor of the hypothesis that porphyry copper deposits are formed by arc magmas that are normal in terms of initial H₂O contents (this study), Cu contents (Cline and Bodnar, 1991; Chelle-Michou et al., 2017; Chiaradia and Caricchi, 2017; Du and Audétat, 2020), and fO₂ (Lee and Tang, 2020). The results discussed above rather suggest that the occurrence of the Cu-richest deposits in thick arcs is controlled by other processes than an anomalously high initial H₂O content in the primary basalts. Intracrustal evolution and the P-T conditions under which this occurs seem to be the main controlling factor for the formation of porphyry deposits (Chiaradia and Caricchi, 2017). Such intracrustal evolution is controlled by large-scale geodynamic parameters, such as the crustal thickness of the overriding plate (Chiaradia, 2020; Lee and Tang, 2020), the intracrustal stress conditions associated with the interaction between the subducting and overriding plates (Tosdal and Richards, 2001; Richards, 2003), and changes in the tectonic situation (Cooke et al., 2005; Chiaradia et al., 2009; Bertrand et al., 2014; Richards, 2018), which may promote changes in the stress conditions within the crust that, ultimately, could be the most important factor controlling the formation of these deposits.

Data Availability Statement

The Monte Carlo-generated datasets for this study and detailed explanations on how to reproduce them can be found in the Supplementary Data Sheets S1–S3.

Author Contributions

MC designed the research, performed the Monte Carlo simulations, wrote the manuscript, and drafted the figures.

Funding

This study was funded by the Swiss National Foundation (grant N. 200021_169032).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.00138/full#supplementary-material

References

Annen, C. (2009). From plutons to magma chambers: thermal constraints on the accumulation of eruptible silicic magma in the upper crust. Earth Planet Sci. Lett. 284, 409–416. doi: 10.1016/j.epsl.2009.05.006

CrossRef Full Text | Google Scholar

Annen, C., Blundy, J. D., and Sparks, R. S. J. (2006). The genesis of intermediate and silicic magmas in deep crustal hot zones. J. Pet. 47, 505–539. doi: 10.1093/petrology/egi084

CrossRef Full Text | Google Scholar

Barclay, J., and Carmichael, I. S. E. (2004). A hornblende basalt from western mexico: water-saturated phase relations constrain a pressure–temperature window of eruptibility. J. Pet. 45, 485–506. doi: 10.1093/petrology/egg091

CrossRef Full Text | Google Scholar

Bertrand, G., Guillou-Frottier, L., and Loiselet, C. (2014). Distribution of porphyry copper deposits along the western Tethyan and Andean subduction zones: insights from a paleotectonic approach. Ore Geol. Rev. 60, 174–190. doi: 10.1016/j.oregeorev.2013.12.015

CrossRef Full Text | Google Scholar

Burnham, C. W. (1979). “Magmas and hydrothermal fluids,” in Geochemistry of Hydrothermal Ore Deposits, 2nd Edn, ed. H. L. Barnes (New York: Wiley), 71–136.

Google Scholar

Caricchi, L., Simpson, G., and Schaltegger, U. (2014). Zircons reveal magma fluxes in the Earth’s crust. Nature 511, 457–461. doi: 10.1038/nature13532

PubMed Abstract | CrossRef Full Text | Google Scholar

Cashman, K. V., Sparks, R. S. J., and Blundy, J. D. (2017). Vertically extensive and unstable magmatic systems: a unified view of igneous processes. Science 355:eaag3055. doi: 10.1126/science.aag3055

PubMed Abstract | CrossRef Full Text | Google Scholar

Chelle-Michou, C., Chiaradia, M., Ovtcharova, M., Ulianov, A., and Wotzlaw, J.-F. (2014). Zircon petrochronology reveals the temporal link between porphyry systems and the magmatic evolution of their hidden plutonic roots (The Eocene Coroccohuayco deposit, Peru). Lithos 198-199, 129–140. doi: 10.1016/j.lithos.2014.03.017

CrossRef Full Text | Google Scholar

Chelle-Michou, C., Rottier, B., Caricchi, L., and Simpson, G. (2017). Tempo of magma degassing and the genesis of porphyry copper deposits. Sci. Rep. 7:40566.

Google Scholar

Chen, K., Tang, M., Lee, C.-T. A., Wang, Z., Zou, Z., Hu, Z., et al. (2020). Sulfide-bearing cumulates in deep continental arcs: the missing copper reservoir. Earth Planet Sci. Lett. 531:115971. doi: 10.1016/j.epsl.2019.115971

CrossRef Full Text | Google Scholar

Chiaradia, M. (2014). Copper enrichment in arc magmas controlled by overriding plate thickness. Nat. Geosci. 7, 43–46. doi: 10.1038/ngeo2028

CrossRef Full Text | Google Scholar

Chiaradia, M. (2015). Crustal thickness control on Sr/Y signatures of recent arc magmas: an earth scale perspective. Sci. Rep. 5:8115.

Google Scholar

Chiaradia, M. (2020). Gold endowments of porphyry deposits controlled by precipitation efficiency. Nat. Comm. 11:248.

Google Scholar

Chiaradia, M., and Caricchi, L. (2017). Stochastic modelling of deep magmatic controls on porphyry copper deposit endowment. Sci. Rep. 7:44523.

Google Scholar

Chiaradia, M., Merino, D., and Spikings, R. (2009). Rapid transition to long-lived deep crustal magmatic maturation and the formation of giant porphyry-related mineralization (Yanacocha, Peru). Earth Planet Sci. Lett. 288, 505–515. doi: 10.1016/j.epsl.2009.10.012

CrossRef Full Text | Google Scholar

Chiaradia, M., Schaltegger, U., Spikings, R. A., Wotzlaw, J. F., and Ovtcharova, M. (2013). How accurately can we date the duration of magmatic-hydrothermal events in porphyry systems? Econ. Geol. 108, 565–584. doi: 10.2113/econgeo.108.4.565

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiaradia, M., Ulianov, A., Kouzmanov, K., and Beate, B. (2012). Why large porphyry Cu deposits like high Sr/Y magmas? Sci. Rep. 2:685. doi: 10.1038/srep00685

PubMed Abstract | CrossRef Full Text | Google Scholar

Chin, E. J., Shimizu, K., Bybee, G. M., and Erdman, M. E. (2018). On the development of the calc-alkaline and tholeiitic magma series: a deep crustal cumulate perspective. Earth Planet Sci. Lett. 482, 277–287. doi: 10.1016/j.epsl.2017.11.016

CrossRef Full Text | Google Scholar

Cline, J. S., and Bodnar, R. J. (1991). Can economic porphyry copper mineralization be generated by a “typical” calc-alkaline melt? J. Geophys. Res. 96, 8113–8126.

Google Scholar

Cooke, D. R., Hollings, P., and Walshe, J. L. (2005). Giant porphyry deposits: characteristics, distribution, and tectonic controls. Econ. Geol. 100, 801–818. doi: 10.2113/gsecongeo.100.5.801

PubMed Abstract | CrossRef Full Text | Google Scholar

Davidson, J., Turner, S., Handley, H., Macpherson, C., and Dosseto, A. (2007). Amphibole “sponge” in arc crust? Geology 35, 787–790.

Google Scholar

Du, J., and Audétat, A. (2020). Early sulfide saturation is not detrimental to porphyry Cu-Au formation. Geology 48:1130. doi: 10.1130/G47169.1

CrossRef Full Text | Google Scholar

Edmonds, M., Cashman, K. V., Holness, M., and Jackson, M. (2019). Architecture and dynamics of magma reservoirs. Philos. Trans. R. Soc. A 377:20180298. doi: 10.1098/rsta.2018.0298

PubMed Abstract | CrossRef Full Text | Google Scholar

Foden, J. D., and Green, G. H. (1992). Possible role of amphibole in the origin of andesite: some experimental and natural evidence. Contrib. Min. Pet. 109, 479–493. doi: 10.1007/bf00306551

CrossRef Full Text | Google Scholar

Grove, T. L., Elkins-Tanton, L. T., Parman, S. W., Chatterjee, N., Muntener, O., and Gaetani, G. A. (2003). Fractional crystallization and mantle-melting controls on calc- alkaline differentiation trends. Contrib. Mineral. Petrol. 145, 515–533. doi: 10.1007/s00410-003-0448-z

CrossRef Full Text | Google Scholar

Hedenquist, J. W., and Lowenstern, J. B. (1994). The role of magmas in the formation of hydrothermal ore deposits. Nature 370, 519–527. doi: 10.1038/370519a0

CrossRef Full Text | Google Scholar

Heinrich, C. A., Halter, W., Landtwing, M. R., and Pettke, T. (2005). The formation of economic porphyry copper (-gold) deposits: constraints from microanalysis of fluid and melt inclusions. Geol. Soc. Lond. Special Public. 248, 247–263. doi: 10.1144/gsl.sp.2005.248.01.13

CrossRef Full Text | Google Scholar

Hollings, P., Cooke, D., and Clark, A. (2005). Regional geochemistry of Tertiary igneous rocks in Central Chile: implications for the geodynamic environment of giant porphyry copper and epithermal gold mineralization. Econ. Geol. 100, 887–904. doi: 10.2113/gsecongeo.100.5.887

PubMed Abstract | CrossRef Full Text | Google Scholar

Jambon, A. (1994). “Earth degassing and large-scale geochemical cycling of volatile elements,” in Volatiles in Magmas, eds M. R. Carroll and J. R. Holloway (Chantilly: Mineralogical Society of America), 479–517.

Google Scholar

Johnson, E. R., Wallace, P. J., Delgado Granados, H., Manea, V. C., Kent, A. J. R., Bindeman, I. N., et al. (2009). Subduction-related volatile recycling and magma generation beneath central Mexico: insights from melt inclusions, oxygen isotopes and geodynamic models. J. Petrol. 50, 1729–1764. doi: 10.1093/petrology/egp051

CrossRef Full Text | Google Scholar

Kelley, K. A., Plank, T., Newman, S., Stolper, E., Grove, T. L., Parman, S., et al. (2010). Mantle melting as a function of water content beneath the Mariana arc. J. Petrol. 51, 1711–1738. doi: 10.1093/petrology/egq036

CrossRef Full Text | Google Scholar

Langmuir, C. H., Bezos, A., Escrig, S., and Parman, S. W. (2006). “Chemical systematics and hydrous melting of the mantle in back- arc basins,” in Back-arc Spreading Systems: Geological, Biological, Chemical, and Physical Interactions, eds D. M. Christie and C. R. Fisher (Washington, DC: American Geophysical Union), 87–146. doi: 10.1029/166gm07

CrossRef Full Text | Google Scholar

Le Bas, M. J., Le Maitre, R. W., Streckeisen, A., and Zanettin, B. (1986). A chemical classification of volcanic rocks based on the total alkali-silica diagram. J. Pet. 27, 745–750. doi: 10.1093/petrology/27.3.745

CrossRef Full Text | Google Scholar

Lee, C.-T. A., Luffi, P., Chin, E. J., Bouchet, R., Dasgupta, R., Morton, D. M., et al. (2012). Copper systematics in arc magmas and implications for crust–mantle differentiation. Science 336, 64–68. doi: 10.1126/science.1217313

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C.-T. A., and Tang, M. (2020). How to make porphyry copper deposits. Earth Planet Sci. Lett. 529:115868. doi: 10.1016/j.epsl.2019.115868

CrossRef Full Text | Google Scholar

Newman, S., and Lowenstern, J. B. (2002). VolatileCalc: a silicate melt-H2O-CO2 solution model written in visual basic for excel. Comput. Geosci. 28, 597–604. doi: 10.1016/s0098-3004(01)00081-4

CrossRef Full Text | Google Scholar

Perrin, A., Goes, S., Prytulak, J., Rondenay, S., and Davies, D. R. (2018). Mantle wedge temperatures and their potential relation to volcanic arc location. Earth Planet Sci. Lett. 501, 67–77. doi: 10.1016/j.epsl.2018.08.011

CrossRef Full Text | Google Scholar

Plank, T., Kelley, K. A., Zimmer, M. M., Hauri, E. H., and Wallace, P. J. (2013). Why do mafic arc magmas contain ∼4 wt% water on average? Earth Planet Sci. Lett. 364, 168–179. doi: 10.1016/j.epsl.2012.11.044

CrossRef Full Text | Google Scholar

Portnyagin, M., Hoernle, K., Plechov, P., Mironov, N., and Khubunaya, S. (2007). Constraints on mantle melting and composition and nature of slab components in volcanic arcs from volatiles (H2O, S, Cl, F) and trace elements in melt inclusions from the Kamchatka arc. Earth Planet. Sci. Lett. 255, 53–69. doi: 10.1016/j.epsl.2006.12.005

CrossRef Full Text | Google Scholar

Richards, J. P. (2003). Tectono-magmatic precursors for porphyry Cu-(Mo-Au) deposit formation. Econ. Geol. 98, 1515–1533. doi: 10.2113/gsecongeo.98.8.1515

PubMed Abstract | CrossRef Full Text | Google Scholar

Richards, J. P. (2009). Postsubduction porphyry Cu–Au and epithermal Au deposits: products of remelting of subduction-modified lithosphere. Geology 37, 247–250. doi: 10.1130/g25451a.1

CrossRef Full Text | Google Scholar

Richards, J. P. (2011). High Sr/Y arc magmas and porphyry Cu±Mo±Au deposits: just add water. Econ. Geol. 106, 1075–1081. doi: 10.2113/econgeo.106.7.1075

PubMed Abstract | CrossRef Full Text | Google Scholar

Richards, J. P. (2013). Giant ore deposits formed by optimal alignments and combinations of geological processes. Nat. Geosci. 6, 911–916. doi: 10.1038/ngeo1920

CrossRef Full Text | Google Scholar

Richards, J. P. (2018). A shake-up in the porphyry world? Econ. Geol. 113, 1225–1233. doi: 10.5382/econgeo.2018.4589

CrossRef Full Text | Google Scholar

Richards, S. W., and Holm, R. J. (2013). Tectonic preconditioning and the formation of giant porphyry deposits. SEG Special Public. 17, 265–275. doi: 10.5382/sp.17.08

CrossRef Full Text | Google Scholar

Rodríguez, C., Sellés, D., Dungan, M., Langmuir, C., and Leeman, W. (2007). Adakitic dacites formed by intracrustal crystal fractionation of water-rich parent magmas at Nevado de Longaví volcano (36.2°S; Andean Southern Volcanic Zone, Central Chile). J. Petrol. 48, 2033–2061. doi: 10.1093/petrology/egm049

CrossRef Full Text | Google Scholar

Rosenbaum, G., Giles, D., Saxon, M., Betts, P. G., Weinberg, R. F., and Duboz, C. (2005). Subduction of the nazca ridge and the inca plateau: insights into the formation of ore deposits in Peru. Earth Planet Sci. Lett. 239, 18–32. doi: 10.1016/j.epsl.2005.08.003

CrossRef Full Text | Google Scholar

Ruscitto, D. M., Wallace, P. J., Johnson, E. R., Kent, A. J. R., and Bindeman, I. N. (2010). Volatile contents of mafic magmas from cinder cones in the central oregon high cascades: implications for magma formation and mantle conditions in a hot arc. Earth Planet Sci. Lett. 298, 153–161. doi: 10.1016/j.epsl.2010.07.037

CrossRef Full Text | Google Scholar

Seward, T. M., William-Jones, A. E., and Migdisov, A. A. (2014). “The chemistry of metal transport and deposition by ore-forming hydrothermal fluids,” in Treatise on Geochemistry, 2nd Edn, eds H. Holland and K. Turekian (Amsterdam: Elsevier), 29–57. doi: 10.1016/b978-0-08-095975-7.01102-5

CrossRef Full Text | Google Scholar

Sillitoe, R. H. (2010). Porphyry copper systems. Econ. Geol. 105, 3–41. doi: 10.2113/gsecongeo.105.1.3

PubMed Abstract | CrossRef Full Text | Google Scholar

Stern, C. R., Skewes, M. A., and Arevalo, A. (2010). Magmatic evolution of the giant el teniente Cu-Mo deposit, central chile. J. Pet. 52, 1591–1617. doi: 10.1093/petrology/egq029

CrossRef Full Text | Google Scholar

Tosdal, R. M., and Richards, J. P. (2001). Magmatic and structural controls on the development of porphyry Cu ± Mo ± Au deposits. Rev. Econ. Geol. 14, 157–181. doi: 10.5382/rev.14.06

CrossRef Full Text | Google Scholar

Turner, S. J., and Langmuir, C. H. (2015). What processes control the chemical compositions of arc front stratovolcanoes? Geochem. Geophys. Geosyst. 16, 1865–1893. doi: 10.1002/2014gc005633

CrossRef Full Text | Google Scholar

Turner, S. J., Langmuir, C. H., Katz, R. F., Dungan, M. A., and Escrig, S. (2016). Parental arc magma compositions dominantly controlled by mantle-wedge thermal structure. Nat. Geosci. 9, 772–776. doi: 10.1038/ngeo2788

CrossRef Full Text | Google Scholar

Wilkinson, J. J. (2013). Triggers for the formation of porphyry ore deposits in magmatic arcs. Nat. Geosci. 6, 917–925. doi: 10.1038/ngeo1940

CrossRef Full Text | Google Scholar