- 1Department of Earth and Environmental Studies, Montclair State University, Montclair, NJ, United States
- 2Geology & Geophysics Department, Woods Hole Oceanographic Institution, Woods Hole, MA, United States
Submerged barrier deposits preserved on continental shelf seabeds provide a record of paleocoastal environmental change from the last glacial maximum through the Holocene. The formation of these offshore deposits is often attributed to intermittent periods of rapidly rising sea levels, especially glacial meltwater pulses, which are expected to lead to partial or complete drowning – overstepping – of migrating barrier islands. However, recent cross-shore modeling and field evidence suggests that even for constant sea-level rise and shelf slope, the internal dynamics of migrating barriers could plausibly drive periodic retreat accompanied by autogenic partial overstepping and deposition of barrier sediment. We hypothesize that the interaction of periodic retreat with changes in external (allogenic) forcing from sea-level rise may create novel retreat responses and corresponding relict barrier deposits. Specifically, we posit that autogenic deposits can be amplified by an increased rate of relative sea-level rise, while in other cases internal dynamics can disrupt or mask the production of allogenic deposits. Here, we model barriers through a range of autogenic–allogenic interactions, exploring how barriers with different inherent autogenic periods respond to discrete, centennial-scale sea-level-rise pulses of variable magnitude and timing within the autogenic transgressive barrier cycle. Our results demonstrate a diversity of depositional signals, where production of relict sands is amplified or suppressed depending on both the barrier’s internal dynamic state and the pulse magnitude. We also show that millennial-scale autogenic periodicity renders barriers vulnerable to complete drowning for relatively low pulse rates of rise (<15 mm/year).
Introduction
Submerged and remnant transgressive barrier island deposits can be a major component of shelf bathymetry and stratigraphy, commonly found on continental shelves across the world (Rampino and Sanders, 1980; Mellett et al., 2012a; De Falco et al., 2015). Formation of these barrier deposits is typically attributed to changes in allogenic forcing, such as changes in the rate of sea-level rise, alteration of sediment supply, or variation in antecedent topography (Cattaneo and Steel, 2003; Storms et al., 2008; Mellett et al., 2012a). Because these drowned or “overstepped” barrier features are associated with variations in external environmental (allogenic) forcing, recent studies have investigated them to gain insights into how modern barriers might respond to future environmental changes, for example, an increase in rate of relative sea-level rise (Donoghue, 2011; Cooper et al., 2016; Emery et al., 2019; Mulhern et al., 2019). Understanding how barrier systems previously responded to periods of increased sea-level rise can also help inform future socioeconomic risks. This is particularly pertinent because centennial-scale processes driving transgressive barrier evolution are not well understood or commonly considered in modern coastal management (Cooper et al., 2018; Cowell and Kinsela, 2018; McNamara and Lazarus, 2018).
Recently, morphodynamic modeling of barriers by Lorenzo-Trueba and Ashton (2014) and modeling with field comparison by Ciarletta et al. (2019) have implicated internally driven (autogenic) periodic retreat as a plausible agent of remnant barrier deposition. This periodic mode of retreat, common for many barrier configurations, is defined by alternating episodes of migration and aggradation, driven by a temporal lag in shoreface response to overwash. During the transition from aggradation to migration, a portion of the lower shoreface is stranded on the continental shelf, producing a deposit of relict barrier sand (Ciarletta et al., 2019).
While not invoking the same mechanism, the deposition of barrier sands during landward migration was initially conceptualized in a series of studies and replies by Rampino and Sanders (1980, 1981, 1982, 1983), who described a drowned barrier system off of the coast of Long Island, NY, United States. Specifically, their work suggested that a rapid increase in the rate of relative sea-level rise could induce complete drowning and overstepping of a barrier, or potentially trigger a mode of combined partial overstepping and retreat (Rampino and Sanders, 1982). The latter concept is intriguing, with Rampino and Sanders (1982) detailing a scenario in which a barrier aggrades during rapid sea-level rise before later undergoing migration (as aggradation increasingly fails to maintain pace with rise). In the context of the Long Island system, the authors referred to this process as a means to describe how both lower shoreface and back-barrier lagoon sediments could be preserved on the modern shelf seabed (Rampino and Sanders, 1983). Earlier, it had been assumed that barriers retreat primarily as steady-state phenomena (Swift, 1975), precluding partial overstepping behaviors. More recently, the acknowledgment that barriers experience variable phases of retreat, potentially resulting in complex future changes in response to increasing sea-level rise, has led to renewed interest in the evolution of barriers at centennial scales (Cooper et al., 2018). This interest is further motivated by the increasing number of globally distributed drowned barrier deposits observed in different geologic settings (Mellett and Plater, 2018).
Whereas Rampino and Sanders (1982) suggested externally driven sediment supply as a mechanism to provide for aggradation even under rapid sea-level rise, we theorize that autogenically driven periodic barrier retreat provides another means for barrier aggradation to coincide with a rapid increase in sea-level rise. To evaluate this hypothesis, we model periodically retreating barriers subjected to high magnitude, century-scale “pulses” in the rate of sea-level rise. Such pulses occurred commonly during the late Pleistocene and early Holocene due to episodes of enhanced glacial melt and possible glacial outburst floods (Liu and Milliman, 2004). We later compare modeled deposits with barrier remnants observed in nature, as well as briefly consider the impact of enhanced sea-level rise on modern barriers.
Materials and Methods
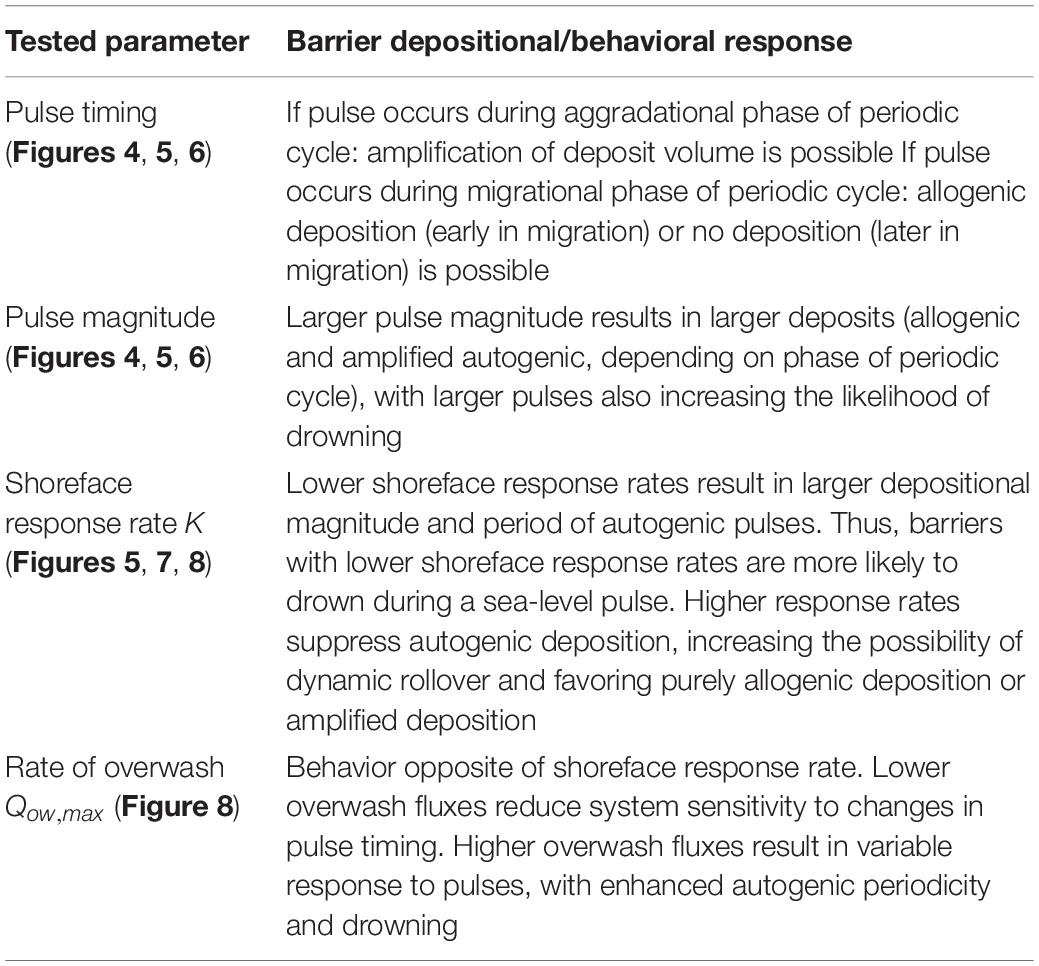
Interplay of Autogenic and Allogenic Forcing
We are partly inspired to model a periodically retreating barrier subjected to a rapid increase in relative sea-level rise based on a recently compiled set of chronologically controlled drowned barriers (Mellett and Plater, 2018) that correlate in time with a sea-level-rise pulse (or pulses) associated with the 8.2 kyr event – an abrupt cooling of global climate linked to glacial lake outburst floods and enhanced meltwater runoff during the collapse of the Laurentide Ice Sheet (LIS) (Hijma and Cohen, 2010; Mellett and Plater, 2018). The timing, duration, and magnitude of the pulse(s) associated with the 8.2 kyr event remains an active area of research [and to varying degrees depends on the location within the global ocean due to the effects of glacial isostatic adjustment (Kendall et al., 2008; Whitehouse, 2018)], but Hijma and Cohen (2010), using sea-level index points derived from radiocarbon dating of basal peats in Rotterdam (NL), suggest a pulse beginning 8450 ± 44 years BP with a magnitude of 2.11 ± 0.89 m over 200 years – an average rate of rise of 10.6 mm/year. Lawrence et al. (2016) additionally identified this pulse using microfossils at the Cree Estuary in Scotland, potentially finding a succession of up to three pulses between 8760 and 8218 years BP. This series includes a relatively prominent jump in sea level beginning at 8595 years BP with a mean magnitude of 0.7 m over 130 years – a corresponding average rate of rise of 5 mm/year. For reference, Hijma and Cohen suggest the background rate of rise at Rotterdam was ∼9.75 mm/year, while Lawrence et al. (2016) [using the sea level reconstruction of Bradley et al. (2011)] suggest a background rate of rise at the Cree Estuary between 2 and 3.5 mm/year – in both cases the centennial-scale rate of sea-level rise more than doubled.
How the pulse(s) associated with the 8.2 kyr event potentially interacted with barrier islands during the early-mid Holocene [potentially including the drowned system off Long Island (Rampino and Sanders, 1981)] to create relict deposits remains an open question. If barriers were periodically retreating, the production of remnant deposits – influenced by a combination of autogenic and allogenic forcing – could follow rules of interaction similar to those observed and modeled in alluvial-deltaic systems. In these environments, interpreting environmental signals from the sedimentary record – assigning the driver, timescale, and magnitude of past allogenic forcing – is complicated by internal, non-linear processes affecting deposition and erosion (Foreman and Straub, 2017).
Examining the timescales of autogenic–allogenic interaction in alluvial-deltaic systems using a numerical model, Jerolmack and Paola (2010) demonstrated that environmental (allogenic) signals tend to be preserved in the sedimentary record when they have temporal periods that are longer than the period of autogenic fluctuations. Conversely, allogenically driven variations in deposition are likely to be destroyed if they fall within the timescales of autogenic processes. However, Jerolmack and Paola (2010) also suggest that allogenic signals with periods shorter than the timescales of autogenic processes can be preserved if their magnitudes are large enough to override any autogenic influence. Li et al. (2016), partly exploring this latter case, showed that for deltas this magnitude directly relates to a storage threshold, based on the delta’s spatial extent. Climate signals are attenuated or masked by autogenic processes as the size of the delta system increases in proportion to the depositional potential of allogenic forcing (Li et al., 2016). Modeling of barrier islands by Ciarletta et al. (2019) suggests that periodic deposits with amplitudes (seabed anomalies) greater than half a meter could be expected to occur over centennial to millennial scales, which in the context of alluvial-deltaic studies implies that centennial-scale pulses may have to be relatively high-magnitude to be recorded on the seabed. We explore this thought in the results presented here, modeling a century-scale pulse, but specifically varying the autogenic period of the barrier island and adjusting the pulse timing and magnitude (rate of sea-level rise).
Morphodynamic Model
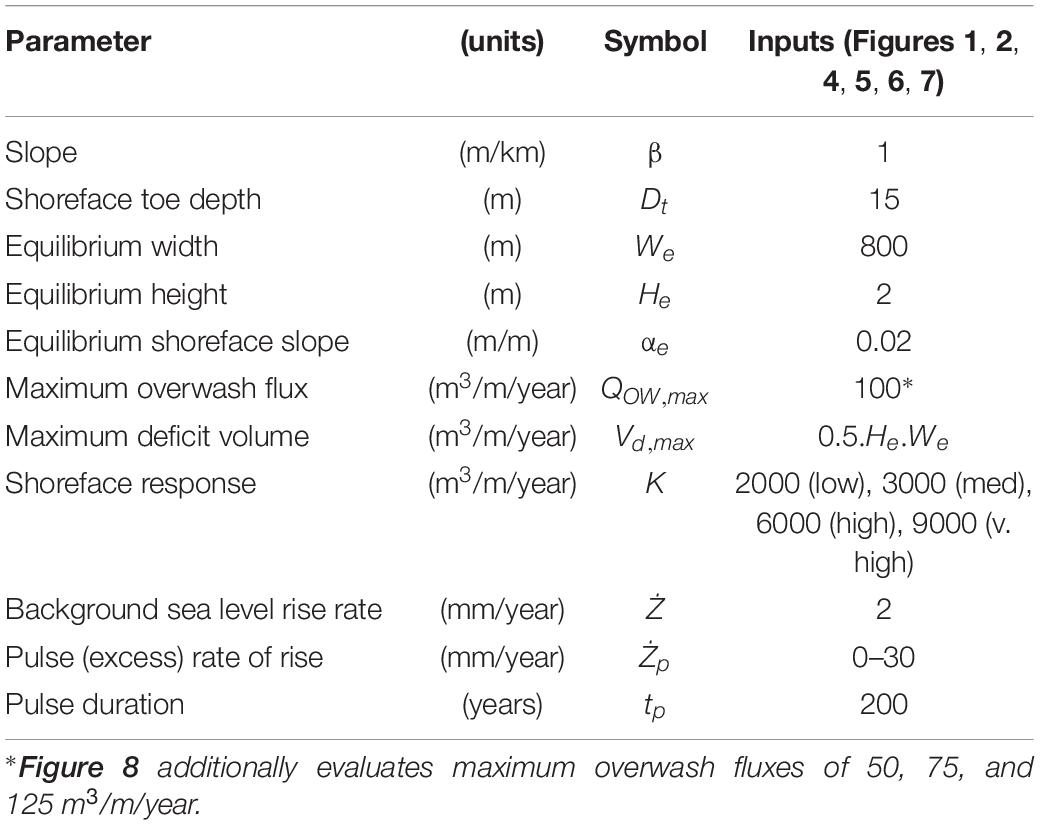
The goal of our work is to explore the diversity of barrier retreat behavior and seabed responses that result from differences in the timing and magnitude of a sea-level pulse interacting with variable internally driven periodicity. We accomplish this by expanding upon Ciarletta et al. (2019), using the cross-shore morphodynamic model of barrier migration by Lorenzo-Trueba and Ashton (2014) – the “LTA” model. Within the LTA model, barrier retreat is governed by the interplay of sea-level rise, shoreface dynamics, and overwash, with cross-shore barrier geometry defined by three moving boundaries: the shoreface toe, ocean shoreline, and backbarrier shoreline (Figure 1). As sea level rises, the barrier height is reduced. In response, barrier shorelines are moved landward by storm-driven overwash, while shoreface dynamics – encapsulated by a shoreface response rate K – adjust the configuration of the shoreface toe and ocean shoreline toward a steady-state geometry. The shoreface toe is additionally constrained by a “depth of closure,” or a depth at which sediment exchange between the seabed and the shoreface is negligible (Hallermeier, 1981).
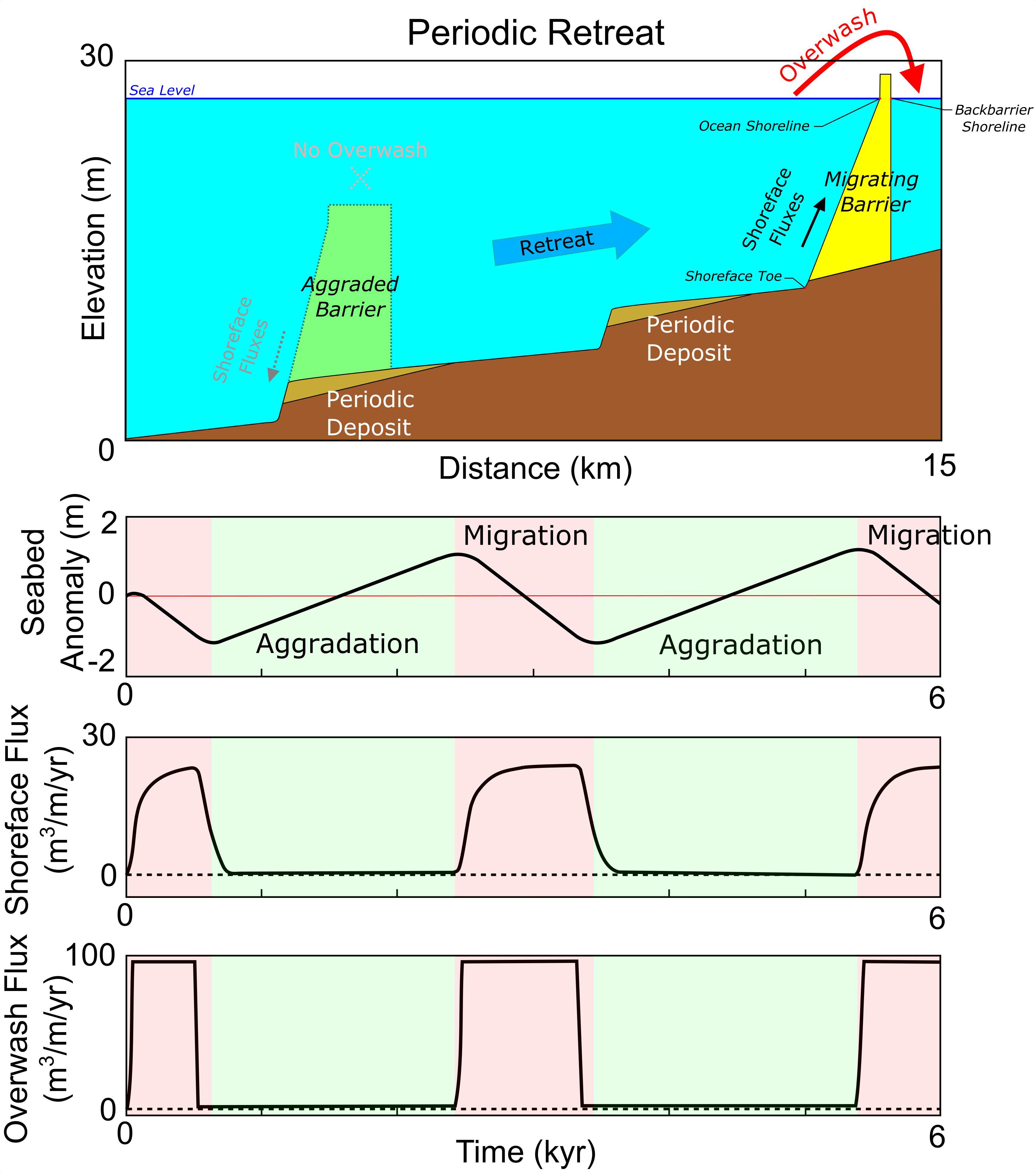
Figure 1. Periodic barrier retreat, defined by an autogenic cycle of alternating episodes of migration (red) and aggradation (green), modeled under constant sea-level rise forcing and shelf slope.
Functionally, the shoreface described by the LTA model spans the portion of the barrier between the shoreface toe and the ocean shoreline, while the “barrier island” comprises the entire structure between the shoreface toe and backbarrier shoreline. As employed in the current study, the model does not consider other processes, such as mass loss or gain driven by alongshore transport gradients [although this process can be accommodated in the model framework (Ashton and Lorenzo-Trueba, 2018)]. This setup reduces the number of environmental variables to isolate the fundamental morphological changes that can be caused by sea-level pulses.
The LTA model can simulate a range of migration and drowning behaviors, including dynamic rollover (constant migration) and periodic retreat. It also captures width drowning, a condition where onshore-directed shoreface fluxes fail to compensate for rapid changes in the geometry of the upper shoreface driven by overwash. Height drowning additionally arises when the rate of sea-level rise outpaces the ability of overwash to maintain the subaerial portion of the barrier.
Physically, periodic retreat is defined by a cycle of aggradation and migration (Figure 1), with the barrier oscillating around an equilibrium profile. During this cycle, as the barrier migrates landward into shallower water, decreasing back-barrier accommodation space and increasing shoreface flux results in widening of the barrier until overwash fluxes no longer reach the back-barrier shoreline. Under rising sea level, such a condition results in aggradation and steepening of the shoreface, with the direction of shoreface fluxes beginning to reverse (“Aggraded Barrier,” Figure 1). The modeling framework would consider this seaward-directed transport to represent net fluxes driven by various wave conditions, with normal storm waves playing the most significant role (Ortiz and Ashton, 2016). Over time, offshore-moving sediment erodes the shoreline while the barrier aggrades in place, causing the barrier to narrow until overwash can again reach the back-barrier shoreline, reinitiating migration (“Migrating Barrier,” Figure 1) and gradually increasing the rate of landward-directed shoreface fluxes, creating a self-reinforced and repeating response.
Modeling Periodic Retreat
In the LTA model, a shoreface response rate is supplied as a constant for the entire shoreface, and subsequently describes the rate at which the lower shoreface will respond to changes in slope in the form of sediment fluxes. This approach is consistent with the study of Ortiz and Ashton (2016), who suggest that changes in the geometry of the upper shoreface by overwash are not immediately translated to changes in the lower shoreface. Specifically, a primary assumption of the LTA model is the existence of an equilibrium shoreface slope, where offshore directed flux (driven by gravity) is balanced by onshore directed flux (driven by wave-driven transport). As the upper shoreface (ocean shoreline) is driven landward by storm-driven overwash it flattens the overall shoreface, and onshore directed transport responds to this out-of-equilibrium geometry as a function of the response rate – estimatable based on wave height/period, grain size/settling velocity, and depth of closure (Lorenzo-Trueba and Ashton, 2014, supplementary materials). A low response rate effectively causes changes in the upper shoreface to be dominated by overwash until the shoreface flattens enough that onshore-directed fluxes can counterbalance landward shoreline advance.
Subsequently, if the shoreface response rate is small relative to the rate of overwash, this increases the temporal lag within the model framework, whereby the barrier experiences increasingly pronounced and sustained deviations from its equilibrium geometry. If the barrier does not drown, these deviations are expressed as cyclical alternations between phases of landward migration and aggradation, creating a regular pattern of ravinement and deposition on the shelf seabed as the barrier geometry oscillates through out-of-equilibrium shoreface configurations (Figure 1). This periodic form of retreat, arising from the morphodynamic nature of the LTA model (Ashton and Lorenzo-Trueba, 2018), is not captured by previous explorations using morphokinematic models, which focus on mass conservation and preservation of (or relaxation to) an idealized barrier geometry as sea level rises (Cowell et al., 1995; Stolper et al., 2005; Moore et al., 2010). Fundamentally, morphokinematic approaches assume that overwash instantaneously drives a landward sediment flux, whereas, in the LTA, a delayed shoreface response is necessary to drive autogenic periodicity.
Modeling Sea-Level Pulses
Within the LTA model, we simulate a pulse inspired by sea-level rise associated with 8.2 kyr event over a 200-year interval (Figure 2), exploring a range of pulse magnitudes from 0 to 30 mm/year with a background rate of sea-level rise of 2 mm/year. This background rate is comparable to that of modern Holocene eustatic rise, as well as the background rate at the Cree Estuary during the 8.2 kyr event (Lawrence et al., 2016). We choose 0–30 mm/year for our pulse magnitudes in light of insights from Liu and Milliman (2004) who suggest that earlier glacial meltwater pulses had mean rates of rise of an order of magnitude higher than observed modern sea-level rise. We also consider that tests with the LTA model suggest rates of rise in excess of 30 mm/year generally result in complete drowning of the barrier system over a 200-year interval. Functionally, the pulse injected into the model has a highly simplified square wave or “top-hat pulse” profile, in which the pulse rate of rise is constant for the pulse duration, simulating the mean pulse described by Hijma and Cohen (2010) (Figure 2).
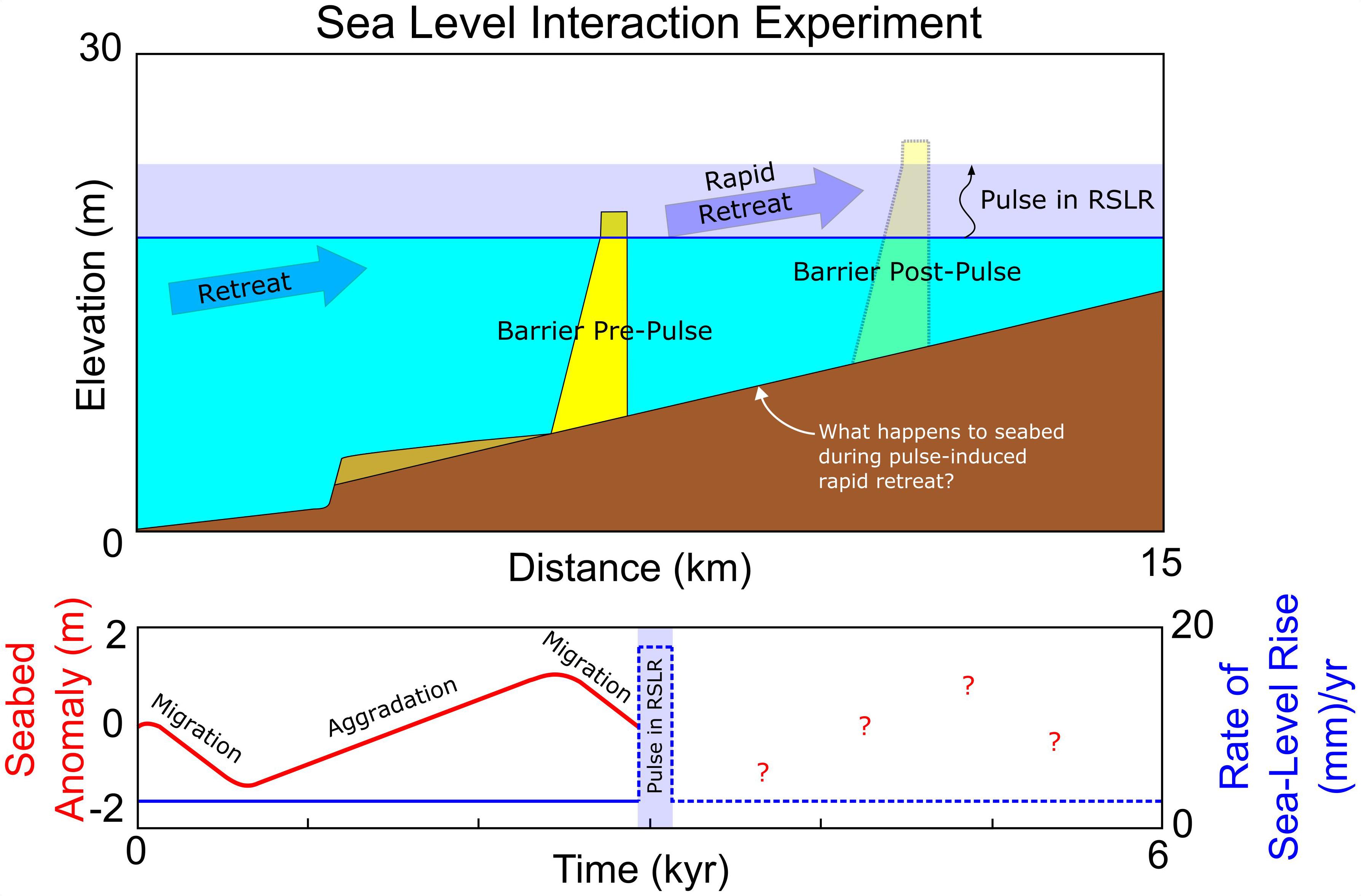
Figure 2. Setup of sea-level interaction experiment. A periodically retreating barrier encounters a pulse in the rate of sea-level rise (in this case, 18 mm/year) for 200 years (comparable to the estimated duration of the 8.2 kyr rise event). To explore autogenic–allogenic interactions, the timing of the pulse is shifted to different times within the periodic cycle (migration and aggradation).
We explore pulse interaction with periodicity in four steps, modeling a transgressive barrier with an equilibrium geometry described by Ciarletta et al. (2019) on a shelf slope of 1 m/km (Table 1). In our initial results, we create a baseline reference (no periodicity) by subjecting a barrier in dynamic rollover to a pulse. Next, we begin to explore pulse interaction with a periodically retreating barrier, altering the timing of pulse initiation with respect to the start of the model run, such that the pulse occurs during different phases of the aggradation and migration cycle (Figure 2, lower panel). Later, we explore how this interaction affects barrier drowning, adjusting the timing and magnitude of the pulse for different rates of shoreface response (increasing/decreasing periodicity). Finally, we characterize the barrier’s behavior as recorded by the seabed and consider the combined effect of different shoreface response rates and maximum overwash fluxes.
Results
Effect of a Pulse on a Rollover Barrier
As a reference case, we initially model the barrier with a “very high” shoreface response rate – for this rate, the barrier is in dynamic rollover, as there is almost no lag between the shoreface response and overwash. This dynamic rollover behavior is similar to the response that could be assumed under a morphokinematic approach, with the barrier assuming a constant steady-state geometry as it retreats (expect for minor fluctuations immediately after initialization) (Figure 3A). Subjecting this smoothly transgressing barrier to a 20 mm/year magnitude pulse (Figure 3B) temporarily disturbs the barrier from its steady state, creating purely allogenically driven deposition with a seabed anomaly “amplitude” over 2 m, followed by corresponding ravinement. In this case, the 200-year sea-level-rise pulse results in barrier response that persists for >1000 years.
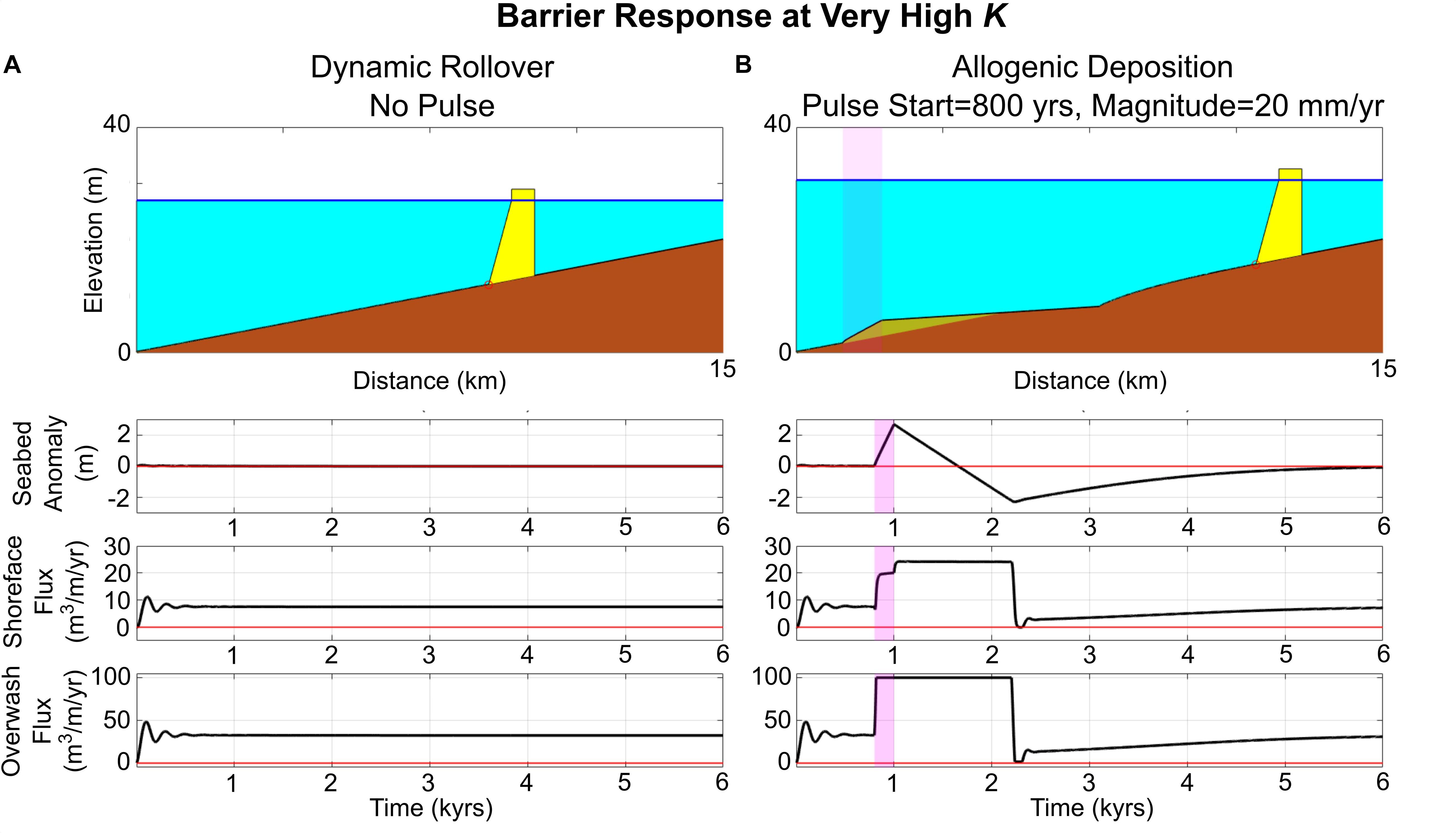
Figure 3. Barrier undergoing dynamic rollover at a very high shoreface response rate K = 9000 m3/m/year. (A) Example with constant forcing and balance between shoreface fluxes and overwash fluxes. (B) The constant rollover barrier is subjected to a 200-year pulse (duration and distance affected highlighted in magenta), beginning 800 years into the model run, with a magnitude of 20 mm/year.
Effect of a Pulse on a Periodically Retreating Barrier
Next, we model a barrier with a “low” shoreface response rate, which, in combination with our other input parameters (Table 1), induces an autogenic periodic cycle lasting ∼2900 years (Figure 4A). By altering the timing of pulse initiation with respect to the start of the model run, the pulse interacts with the barrier’s periodic cycle at different intervals. Our aim is to illustrate the effect of pulse timing on the barrier’s retreat behavior and depositional response.
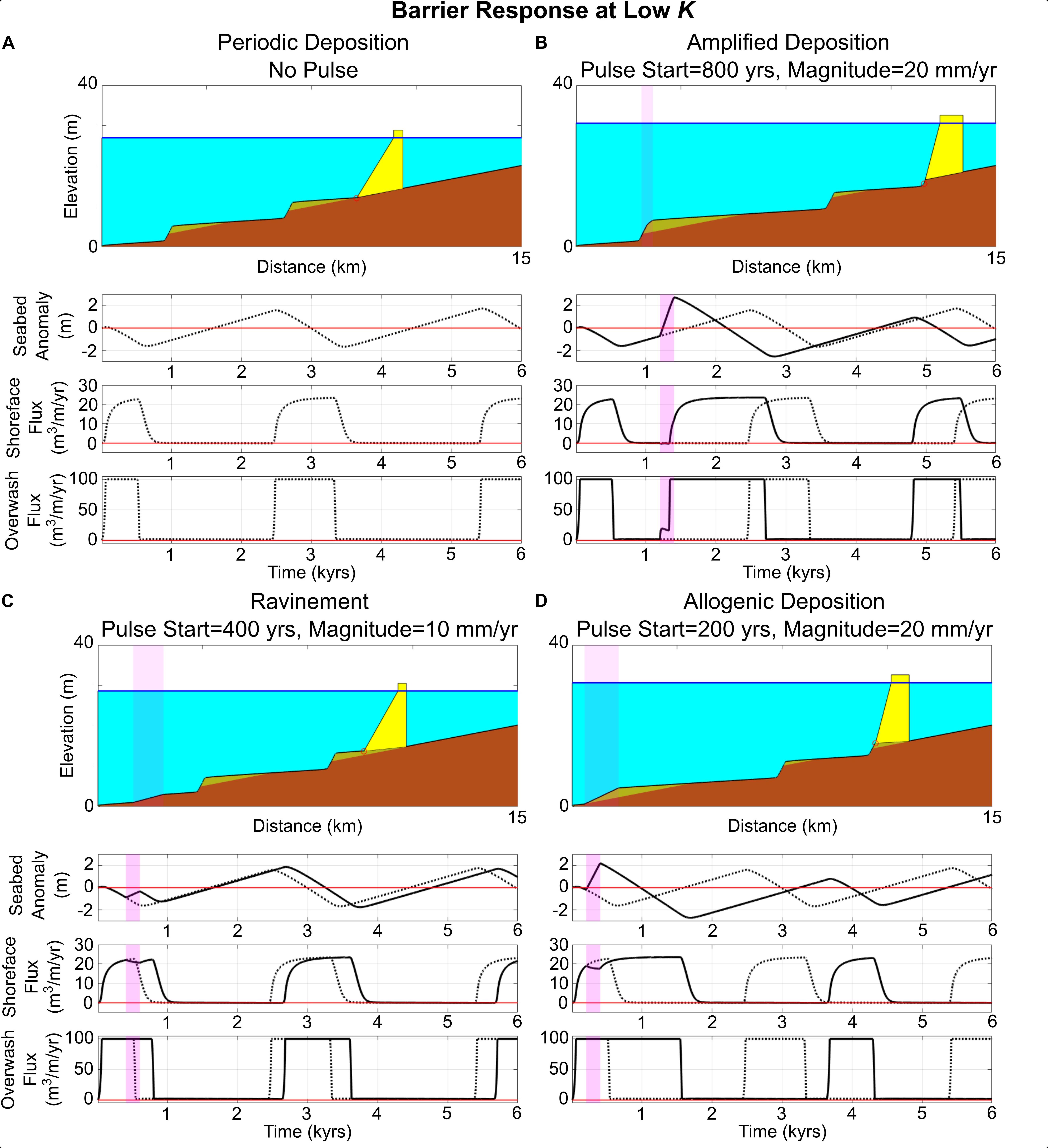
Figure 4. Range of behavioral/depositional responses of a periodically retreating barrier with a low shoreface response rate (K = 2000 m3/m/year) subjected to a pulse in the rate of sea-level rise. Magenta highlights correspond to duration and distance affected by pulse. (A) Periodic deposition (autogenic), with no pulse; dashed lines in subsequent subplots (B–D) refer to subplots shown here. (B) 20 mm/year pulse coinciding with the aggradational phase of periodic retreat; amplified deposit produced. (C) 10 mm/year pulse coinciding with migrational phase of periodic retreat; no deposition/ravinement. (D) 20 mm/year pulse coinciding with migrational phase of periodic retreat; deposition occurs where periodic retreat suggests none should occur.
Varying the timing of applied sea-level-rise pulses for a periodically retreating barrier yields diverse behaviors and different types of deposit production during and after pulse interaction (Figure 4). For example, where the barrier is in the aggradational phase of the periodic cycle (Figure 4A), interaction with a pulse (Figure 4B) initially causes the barrier to accelerate its vertical growth due to the sudden increase in height accommodation. At the same time, the barrier begins eroding at the shoreward edge, until its width becomes narrow enough that it eventually migrates landward. This sequence of events can be seen in the double-step that occurs in the overwash flux, with shoreface fluxes beginning to increase in tandem with the second step (when pulse-induced migration begins). Such an interaction can amplify the height of already-forming autogenic deposits (Figure 4B).
Conversely, if the barrier is in the migrational phase of the periodic cycle when the pulse occurs, interaction with the pulse can lead to two different outcomes (Figures 4C,D). First, if the pulse occurs late enough in the migrational phase, then the pulse will not induce deposition (Figure 4C) – the shoreface is already responding to migration due to overwash, and the pulse simply prolongs this overwash cycle. However, if the pulse occurs earlier in the migrational phase, when the shoreface is only beginning to respond, then the pulse can induce deposition when none would be expected based on the autogenic cycle – a deposit is allogenically forced by the sea-level pulse (Figure 4D).
Effect of Pulse Timing and Shoreface Response Rates on Barrier Drowning
To further explore the influence of autogenic periodicity on behavioral response, we model sea-level pulses of variable timing and magnitude interacting with periodically retreating barriers across a range of shoreface response rates. In particular, we seek to determine under what conditions a sea-level pulse can lead to drowning of a barrier that would otherwise be expected to maintain itself during transgression. Model results suggest that the likelihood of drowning is affected by both the pulse characteristics (timing and magnitude) and the shoreface response rate (Figure 5).
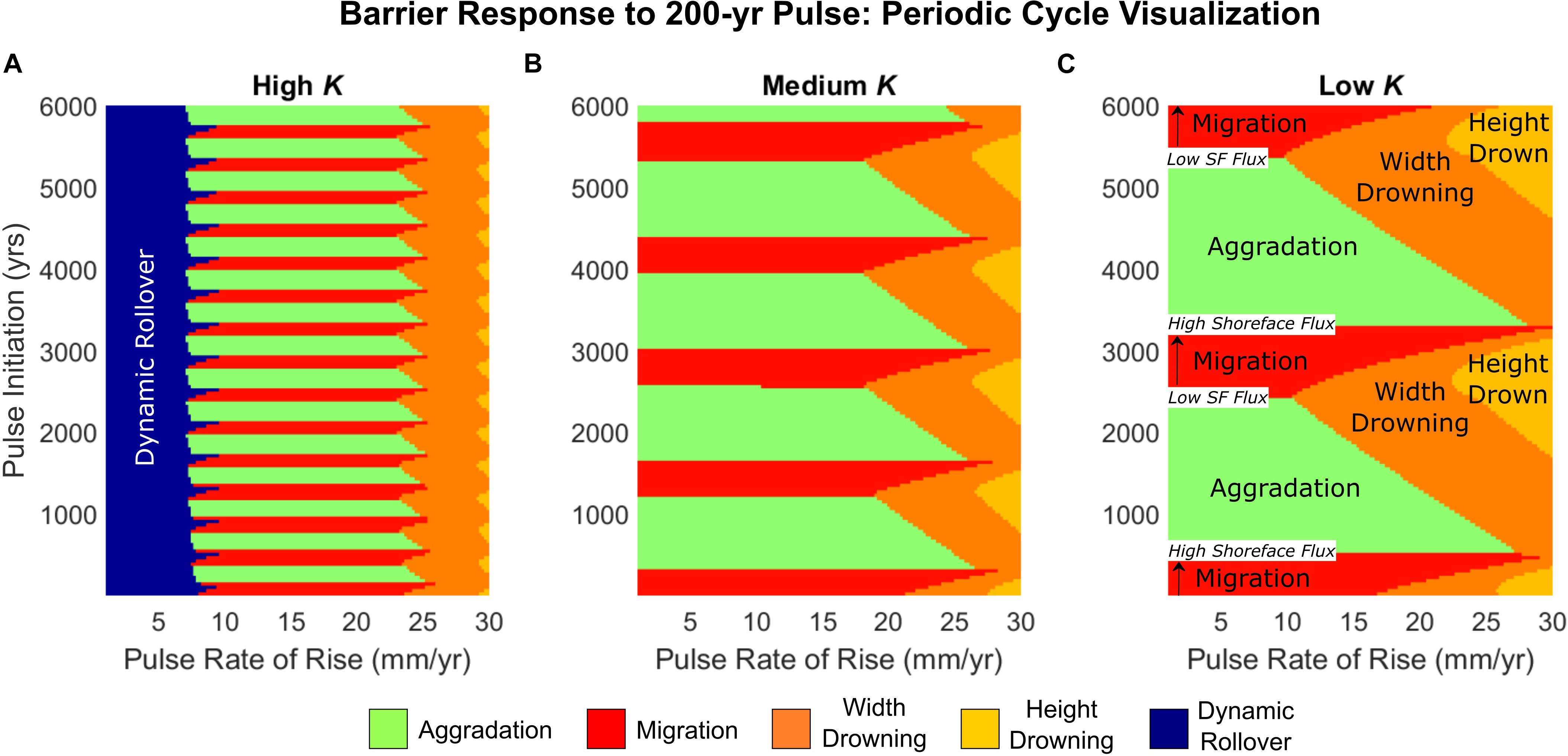
Figure 5. Regime plots depicting the barrier behavioral response to a 200-year sea-level pulse, for different timing of the pulse initiation (relative to the start of the model run) and rate of rise of the pulse. Responses shown for barriers with (A) high K, (B) medium K, and (C) low K (see Table 1). Labels on panel (C) highlight the autogenic cycle of migration-aggradation, which increases in duration at low K (compare panels A–C).
Barrier drowning is more likely for lower shoreface response rates, with pulse timing also strongly affecting whether or not a barrier drowns (Figure 5C). At higher shoreface response rates (Figure 5A), the periodic cycle exerts relatively little influence on whether the barrier drowns; much of the barrier behavior at high shoreface response is also taken up by dynamic rollover at low pulse rates of rise. In all cases (high to low shoreface response rate), complete drowning of the periodically retreating barrier occurs most readily during the transition between aggradation to migration, when landward-directed shoreface fluxes are initially slow to catch up to overwash fluxes and backbarrier accommodation is maximized. Conversely, complete drowning of the barrier can be mitigated if the pulse occurs during the transition between migration to aggradation, where landward-directed shoreface fluxes are peaking and backbarrier accommodation is reduced.
Seabed Response to Pulses
For our final model explorations, we more closely examine the influence of pulse and barrier characteristics (both shoreface response and overwash rates) on the seabed response by constructing a detailed classification of corresponding seabed deposition for different pulse magnitudes and timing. We begin by exploring a barrier with a low shoreface response rate for a full periodic cycle of migration-aggradation (Figure 5C; cycle). For barriers that do not drown, we then determine the maximum amplitude of the seabed deposits. If the deposit amplitudes are larger than those that occur during periodic retreat, or deposition occurs when the periodic cycle indicates there should be ravinement, we classify the deposit as “allogenic” in origin – created partly or solely in response to forcing from sea-level rise (Figure 6). When allogenic deposition coincides with the aggradational phase of periodic retreat, the results are classified as “amplified deposits” (e.g., Figure 4B), or more accurately, periodic deposits with enhanced amplitudes. Conversely, when allogenic deposits are produced during the migrational phase, the results are classified as “emergent” to “large” allogenic deposits (Figure 4D). We define emergent allogenic deposits as having amplitudes smaller than periodic deposits, while large allogenic deposits equal or exceed periodic deposit amplitudes.
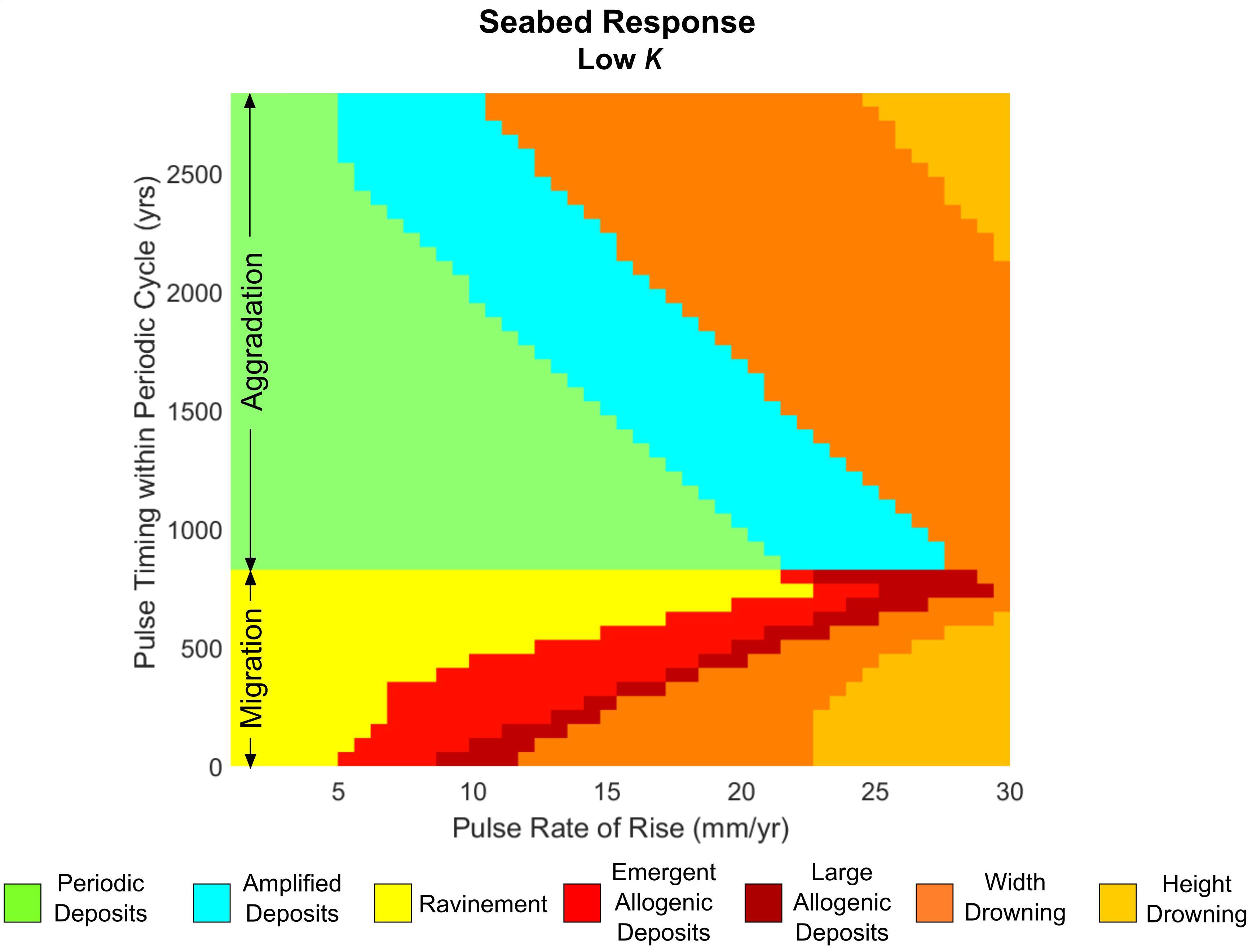
Figure 6. Seabed response classification of a full periodic cycle (migration-aggradation) based on the amplitudes of resulting deposits.
Next, we explore how differences in shoreface response rate affect seabed deposition. A comparison of seabed response at high to low shoreface response rates (Figure 7) shows that a barrier with a high shoreface response rate exhibits a relatively simple response regime (compare High K with Low K), characterized mainly by large allogenic deposits resulting from sea-level pulses with magnitudes of 7–25 mm/year. The highly responsive barrier is also unaffected by lower magnitude pulses (below 7–10 mm/year), remaining in a mode of dynamic rollover. Periodic deposition is almost non-existent at high K and cannot be reliably detected, which explains the lack of amplified deposits.
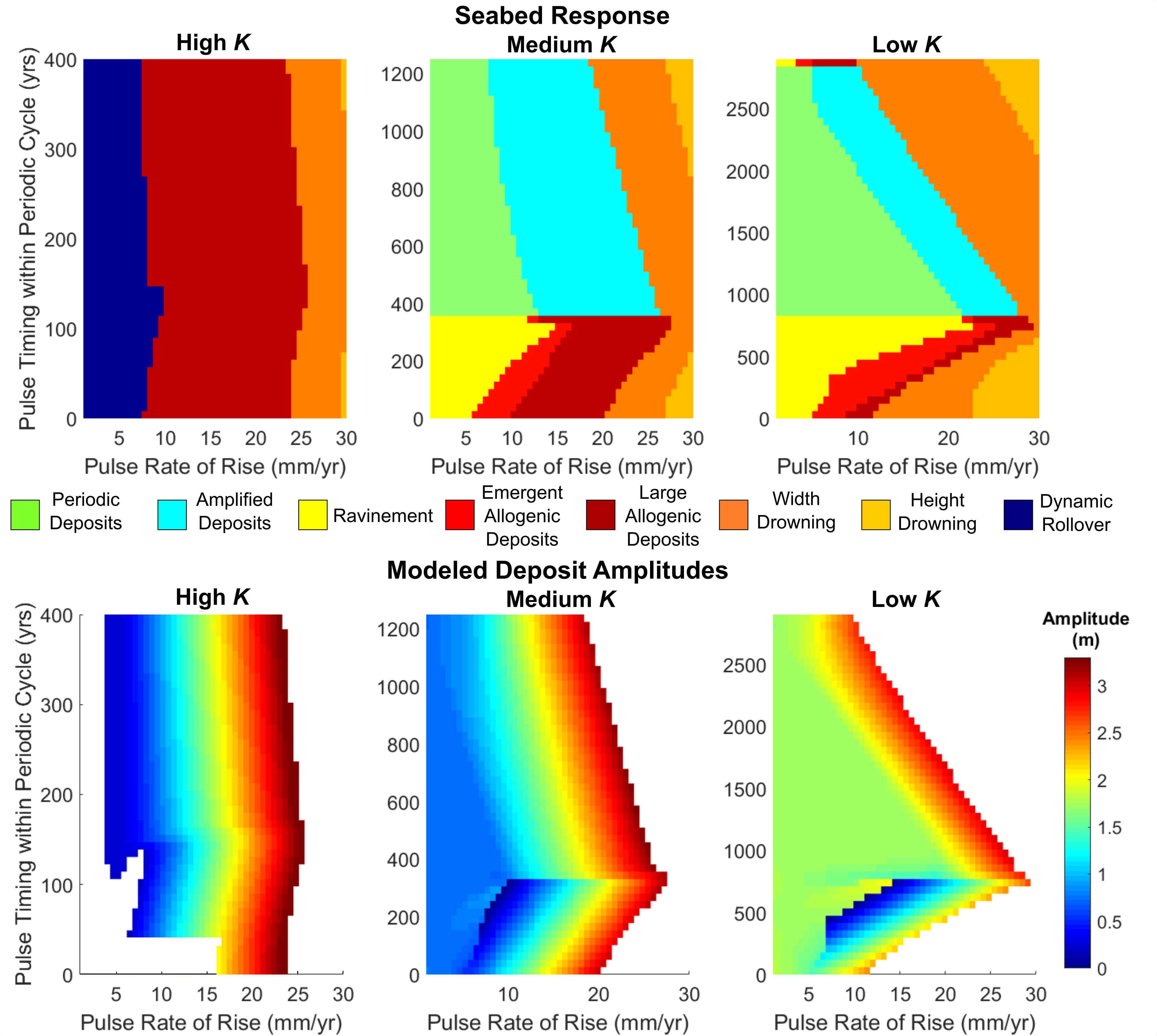
Figure 7. Top: classification of a full periodic cycle with increasing autogenic influence. Bottom: corresponding plots of deposit amplitude. White regions in amplitude plots indicate no detection of a deposit or complete drowning of the barrier.
As suggested by Figure 6, the presence of the periodic cycle, in combination with decreasing shoreface response rate, increasingly limits the production of allogenic deposits. With lower shoreface response rate there is also no dynamic rollover for any pulse magnitude, with periodic deposition/ravinement and drowning the most likely responses. We note more generally that, for all shoreface response rates, the greatest deposit amplitudes occur when barriers are close to the width drowning regime (Figure 7, bottom panel).
To broaden our investigation, we also test the sensitivity of seabed response to different values of the maximum overwash rate (Figure 8). In terms of mediating allogenic versus autogenic deposition, the rate of overwash operates inversely to the shoreface response rate, in that increased overwash induces more temporal lag across the barrier shoreface – this enhances the periodic response at higher rates of overwash. Our sensitivity analysis shows that maximum overwash rates from 50 to 125 m3/m/year can induce seabed responses during pulse interaction that are comparable to our results with variable shoreface response rate. Moreover, where a high overwash rate compounds with low shoreface response rate, the modeled barrier is especially vulnerable to width drowning for even low pulse magnitudes (Figure 8, lower right). Conversely, the co-occurrence of high shoreface response rate and low overwash rate results in a uniform response to increasing pulse magnitude, the barrier rendered insensitive to pulse timing and all deposition driven solely by change in the rate of sea-level rise (Figure 8, upper left).
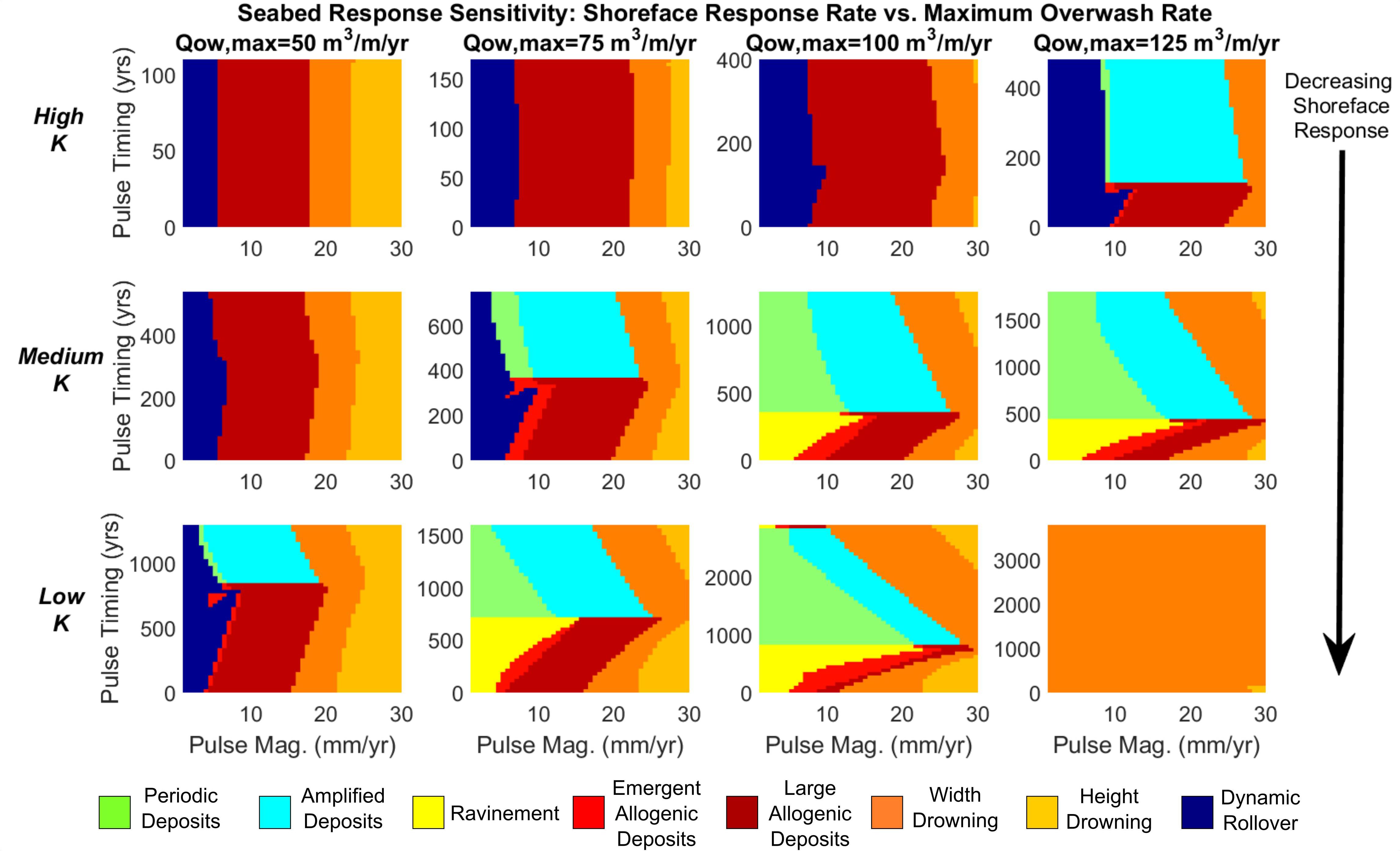
Figure 8. Classification of seabed response based on variable shoreface response rate, maximum overwash rate, sea-level pulse magnitude, and sea-level pulse timing (within a periodic cycle). Shoreface response rate decreases top to bottom (rows), while maximum overwash rate (Qow,max) decreases right to left (columns).
Discussion
Our model results suggest barrier island response to a sea-level pulse is governed by the pulse magnitude, the timing of the pulse, and the interaction of barrier shoreface response rate with overwash (Figure 9 and Table 2). By adjusting each parameter independently, we explore the relative contribution of both internal (autogenic) and external (allogenic) controls on the long-term retreat behavior of the barrier, as well as the types of deposits produced on the seabed. We believe the results of our model explorations are compatible with the observationally inspired concept put forward by Rampino and Sanders (1982) that barrier island retreat involves a suite of states between rollover and complete drowning that are capable of producing remnant deposits on the seabed. Moreover, our work shows that the internal dynamics of a barrier can create an autogenic filter that, despite being regularly oscillating with phases of aggradation and migration, produces a complicated response on the seabed – particularly when considering pulse magnitude and timing.
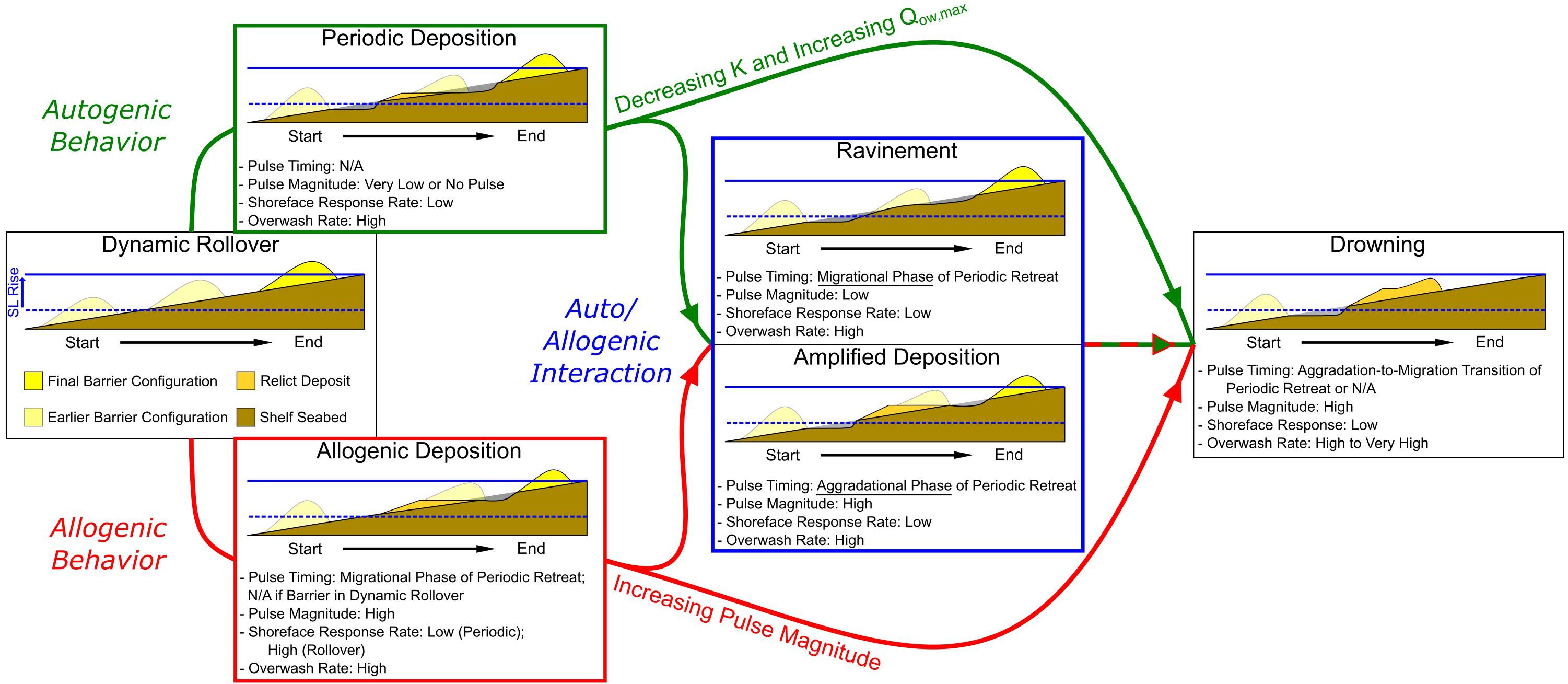
Figure 9. Depiction of barrier response as a function of increasing sea-level pulse magnitude (allogenic behavior – red) and decreasing shoreface response rate K/increasing rate of overwash Qow,max (autogenic behavior – green). Auto/allogenic interaction, where pulses occur in conjunction with periodic deposition, can result in amplified deposits or ravinement, depending on the phase (migrational or aggradational) of periodic retreat and the magnitude of the sea-level pulse. Increasing pulse magnitude, as well as decreasing shoreface response/increasing rate of overwash, ultimately result in barrier drowning. Note that thresholds in internal and external forcing that result in drowning during auto/allogenic interaction are highly variable and depend on the timing of the interaction (see Figure 8). Red and green arrows only represent the relative pathways between barrier responses – they do not imply similar forcing magnitudes between interaction and non-interaction response scenarios.
The rules governing this complicated response within the modeled barrier system share similarities with concepts applied to alluvial-deltaic systems by Jerolmack and Paola (2010) and Li et al. (2016), among others. While we do not test pulses of variable duration, our results show that decreasing periodicity, with aggradational/migrational phases scaling toward the duration of our modeled 200-year pulse, results in an increasingly allogenic depositional response. Conversely, with increasing periodicity, the internal dynamics of the barrier act as an autogenic filter, and only relatively high magnitude pulses can produce an allogenic depositional response – however, the range of pulse magnitudes that can produce allogenic deposition is also variable based on the timing of the pulse within the periodic cycle.
While we can model barrier response under autogenic–allogenic interaction, identifying such a signal in real-world seabed deposits is likely to be difficult based on the similar range of deposit amplitudes produced across the input regime space explored in this study (Figure 7). In particular, this suggests that the internal dynamics of barrier islands are superficially similar to deltas in the way they shred the signals of allogenic forcing operating on sub-autogenic timescales (Foreman and Straub, 2017). One possibility to interpret the response of the barrier from relict deposits is to utilize, where available, a more continuous record of deposition, with multiple deposits [e.g., offshore eastern Texas (Rodriguez et al., 2004)]. Although, presently, most known field sites contain either very short sequences of deposits or just one primary deposit (Mellett and Plater, 2018; Ciarletta et al., 2019). Especially for amplified deposition (Figures 4B,D), pulse interaction can produce a noticeable disruption in amplitude during subsequent deposition, suggesting autogenic–allogenic interaction could be inferred in cases where periodicity is already suspected – this could be supplemented, where available, by age control to correlate timing with known pulses, as has already been accomplished for some field sites (e.g., Mellett and Plater, 2018, describing a barrier system that likely drowned during interaction with the 8.2 kyr event rise per Mellett et al., 2012a, b).
It may also be possible to constrain the potential for past auto/allogenic interaction based on determining the shoreface response rate and maximum overwash rate of the barrier system if a modern analog is available (or a paleobarrier can be reconstructed from relict morphology or other data). For example, recent work by Aagaard and Hughes (2017) quantified shoreface response, or more specifically the balance of onshore-offshore transport as it relates to equilibrium slope, from a combination of field measurements and modeling for coastal Denmark. As for paleobarriers, we note that the shoreface response scales partly as a function of time due to increasing depth of closure over longer timescales (Ortiz and Ashton, 2016), which suggests that estimating the lifetime of such systems [e.g., as accomplished by Mellett et al. (2012b) and Storms et al. (2008), among others] could aid in parameterizing this value. Age dating of paleobarriers, in combination with modeling, could also be applicable to modern barriers to gain insight into future evolution, and could help describe the vulnerability or resilience of specific systems to anthropogenic sea-level rise. Periodic barriers with low shoreface response rates (Figures 5–7) are generally more susceptible to drowning during rapid sea-level rise, although in some cases our results demonstrate that they could withstand up to 30 mm/year of rise (although shoreline retreat and overwash rates would be rapid).
We note that, in addition to shoreface response rate, one of the most important components driving the periodic response produced by the LTA model is storm-driven overwash flux – increasing this flux enhances the lag in the shoreface response to overwash, lengthening the periodic cycle and increasing the potential for diverse seabed responses (Figure 8). We use a maximum overwash rate ranging from 50 to 125 m3/m/year in our results (Table 1), which we estimate compares favorably to real-world barriers. For example, calculation of overwash at barrier sites in New Jersey yields long-term rates in the range 0–100 m3/m/year using a storm return interval of 50 years (Miselis and Lorenzo-Trueba, 2017), which is typical for the region (Scileppi and Donnelly, 2007). Of concern, modern climate change, driving the current anthropogenic “pulse” in the rate of sea-level rise, may reduce this return interval and increase the intensity of storms (Emanuel, 2013), potentially driving overwash rates beyond what we model here.
Not accounting for external sediment supply contributions (anthropogenic or natural), we suggest interaction of modern sea-level rise with periodically retreating barriers could lead to more variability in behavioral response than our explorations indicate, as well as increased vulnerability to drowning for systems already experiencing high rates of overwash. Additionally, our model does not account for changes in sediment grain size and availability across the shelf environment, assuming a uniform and sandy substrate during transgression. In comparing with modern barrier systems, we suggest our model is therefore conservative, and reduction in sand availability could further increase drowning potential or lead to enhanced periodicity.
Furthermore, the potential for auto/allogenic interactions to be expressed in globally distributed field sites (both ancient and modern) will be affected by two important considerations – the shelf slope and barrier volume. Antecedent shelf slopes for observed barrier systems cover an order of magnitude range, from less than a meter per kilometer (West Florida; Locker et al., 2003) to around 2 m per kilometer (Long Island; Rampino and Sanders, 1980), and in excess of 5 m per kilometer (South Africa – Salzmann et al., 2013; Pretorius et al., 2016; Sardinia – De Falco et al., 2015). Additionally, the spacing and size of remnant deposits seen in nature (potentially a proxy for barrier volume) is highly variable, for example, with small (<3000 m3/m) deposits found at sub-kilometer spacing (KwaZulu-Natal shelf, South Africa; Pretorius et al., 2016) and large (>12,000 m3/m) deposits spaced across multiple kilometers (New Jersey; Nordfjord et al., 2009). The previous investigation by Ciarletta et al. (2019) showed that, for the barrier dimensions modeled here, antecedent slopes in excess of 3 m per kilometer can result in an abrupt reduction in autogenic periodicity, with a corresponding decrease in deposit size and spacing. However, tests with the model also suggest that smaller barriers with very low shoreface response rates could allow for autogenic partial overstepping on steeper slopes. Such a relationship is intriguing, as recently Green et al. (2018), studying the role of antecedent topography on overstepped deposits in South Africa, suggest that barrier volume is inversely related to shelf slope.
Of relevance to this study, late Pleistocene/early Holocene sea-level pulses are believed to be coincident with the deposition of relatively small remnant barriers found at steeply sloping sites in South Africa and Sardinia (De Falco et al., 2015; Pretorius et al., 2016). Future modeling explorations may therefore provide insight on whether autogenic partial overstepping interacting with sea-level pulses could play a role in driving deposit size/spacing on high-gradient coastlines. Specifically, we plan to examine Green et al.’s (2018) suggestion that a steep shelf may result in enhanced reworking of remnant barrier deposits due to focused transgressive ravinement – a process that could potentially complicate the ability of steeply sloping coasts to retain a reliable record of pulse interaction, even with sequences of deposits.
Conclusion
Using a morphodynamic model, we demonstrate that autogenic periodicity during barrier island migration could act to filter the response of transgressive systems to rapid changes in rate of sea-level rise (pulses). Our results support the suggestion of Rampino and Sanders (1980, 1981, 1982, 1983) that barrier island retreat and drowning comprises of spectrum of responses that can be recorded on the shelf seabed. In some cases, we show that increasing autogenic periodicity can suppress the depositional response from a sea-level-rise pulse. Conversely, adjustments in the timing and magnitude of a pulse during interaction with a periodically retreating barrier can lead to amplification of autogenic deposition, fully allogenic deposition, or complete drowning of the barrier.
We consider that identifying such autogenic–allogenic interaction in the field presents significant challenges, as the amplitudes of individual relict deposits are not sufficient on their own to characterize the contributions of internal dynamics versus external controls. This exploration suggests, however, that a series of relict deposits could more readily record such an interaction, as sea-level-rise pulses affect the amplitudes of successive periodic deposits. As periodicity strongly affects barrier drowning, we also consider that insights from this exploration could be extended to modern transgressive barriers, providing guidance on their relative vulnerability to differing magnitudes of enhanced sea-level rise.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author. A copy of the model script (MATLAB and Python) used in this study, as well as scripts to produce animations and figures, are available at our model development page https://github.com/ciarletd/LTAModel-Extension.
Author Contributions
DC conceived the model experiments, planned the explorations with JL-T, carried out the simulations, and took the lead in writing the manuscript, with critical feedback from JL-T and AA.
Funding
This material is based upon work supported by the National Science Foundation under Grant No. 1518503, and the American Chemical Society Petroleum Research Fund under Grant No. 58817-DNI8 awarded to JL-T; the views presented herein are solely those of the authors and not of the NSF or the ACS PRF.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This manuscript benefited significantly from constructive evaluations by the reviewers. We would also like to acknowledge our colleagues in the MSU Coastal Research Group for their continued support and feedback; Jesse Kolodin, Arye Janoff, Christopher Tenebruso, William Anderson, and Isamar Cortés.
References
Aagaard, T., and Hughes, M. G. (2017). Equilibrium shoreface profiles: a sediment transport approach. Mar. Geol. 390, 321–330. doi: 10.1016/j.margeo.2016.12.013
Ashton, A. D., and Lorenzo-Trueba, J. (2018). “Morphodynamics of barrier response to sea-level rise,” in Barrier Dynamics and Response to Changing Climate, eds L. J. Moore, and A. B. Murray, (Cham: Springer), 277–304. doi: 10.1007/978-3-319-68086-6_9
Bradley, S. L., Milne, G. A., Shennan, I., and Edwards, R. (2011). An improved glacial isostatic adjustment model for the British Isles. J. Q. Sci. 26, 541–552. doi: 10.1002/jqs.1481
Cattaneo, A., and Steel, R. J. (2003). Transgressive deposits: a review of their variability. Earth Sci. Rev. 62, 187–228. doi: 10.1016/s0012-8252(02)00134-4
Ciarletta, D. J., Lorenzo-Trueba, J., and Ashton, A. D. (2019). Mechanism for retreating barriers to autogenically form periodic deposits on continental shelves. Geology 47, 239–242. doi: 10.1130/g45519.1
Cooper, J. A. G., Green, A. N., and Loureiro, C. (2018). Geological constraints on mesoscale coastal barrier behaviour. Glob. Planet. Change 168, 15–34. doi: 10.1016/j.gloplacha.2018.06.006
Cooper, J. A. G., Green, A. N., Meireles, R. P., Klein, A. H., Souza, J., and Toldo, E. E. (2016). Sandy barrier overstepping and preservation linked to rapid sea level rise and geological setting. Mar. Geol. 382, 80–91. doi: 10.1016/j.margeo.2016.10.003
Cowell, P. J., and Kinsela, M. A. (2018). “Shoreface controls on barrier evolution and shoreline change,” in Barrier Dynamics and Response to Changing Climate, eds L. J. Moore, and A. B. Murray (Cham: Springer), 243–275. doi: 10.1007/978-3-319-68086-6_8
Cowell, P. J., Roy, P. S., and Jones, R. A. (1995). Simulation of large-scale coastal change using a morphological behaviour model. Mar. Geol. 126, 45–61. doi: 10.1016/0025-3227(95)00065-7
De Falco, G., Antonioli, F., Fontolan, G., Presti, V. L., Simeone, S., and Tonielli, R. (2015). Early cementation and accommodation space dictate the evolution of an overstepping barrier system during the Holocene. Mar. Geol. 369, 52–66. doi: 10.1016/j.margeo.2015.08.002
Donoghue, J. F. (2011). Sea level history of the northern Gulf of Mexico coast and sea level rise scenarios for the near future. Clim. Change 107:17. doi: 10.1007/s10584-011-0077-x
Emanuel, K. A. (2013). Downscaling CMIP5 climate models shows increased tropical cyclone activity over the 21st century. Proc. Natl. Acad. Sci. U.S.A 110, 12219–12224. doi: 10.1073/pnas.1301293110
Emery, A. R., Hodgson, D. M., Barlow, N. L., Carrivick, J. L., Cotterill, C. J., Mellett, C. L., et al. (2019). Topographic and hydrodynamic controls on barrier retreat and preservation: an example from Dogger Bank, North Sea. Mar. Geol. 416:105981. doi: 10.1016/j.margeo.2019.105981
Foreman, B. Z., and Straub, K. M. (2017). Autogenic geomorphic processes determine the resolution and fidelity of terrestrial paleoclimate records. Sci. Adv. 3:e1700683. doi: 10.1126/sciadv.1700683
Green, A. N., Cooper, J. A. G., and Salzmann, L. (2018). The role of shelf morphology and antecedent setting in the preservation of palaeo-shoreline (beachrock and aeolianite) sequences: the SE African shelf. Geo Mar. Lett. 38, 5–18. doi: 10.1007/s00367-017-0512-8
Hallermeier, R. J. (1981). Seaward Limit of Significant Sand Transport by Waves: An Annual Zonation for Seasonal Profiles (No. CERC-CETA-81-2). Fort Belvoir, VA: Coastal Engineering Research Center.
Hijma, M. P., and Cohen, K. M. (2010). Timing and magnitude of the sea-level jump preluding the 8200 yr event. Geology 38, 275–278. doi: 10.1130/g30439.1
Jerolmack, D. J., and Paola, C. (2010). Shredding of environmental signals by sediment transport. Geophys. Res. Lett. 37:L19401.
Kendall, R. A., Mitrovica, J. X., Milne, G. A., Törnqvist, T. E., and Li, Y. (2008). The sea-level fingerprint of the 8.2 ka climate event. Geology 36, 423–426.
Lawrence, T., Long, A. J., Gehrels, W. R., Jackson, L. P., and Smith, D. E. (2016). Relative sea-level data from southwest Scotland constrain meltwater-driven sea-level jumps prior to the 8.2 kyr BP event. Quat. Sci. Rev. 151, 292–308. doi: 10.1016/j.quascirev.2016.06.013
Li, Q., Yu, L., and Straub, K. M. (2016). Storage thresholds for relative sea-level signals in the stratigraphic record. Geology 44, 179–182. doi: 10.1130/g37484.1
Liu, J. P., and Milliman, J. D. (2004). Reconsidering melt-water pulses 1A and 1B: global impacts of rapid sea-level rise. J. Ocean Univ. China 3, 183–190. doi: 10.1007/s11802-004-0033-8
Locker, S. D., Hine, A. C., and Brooks, G. R. (2003). Regional stratigraphic framework linking continental shelf and coastal sedimentary deposits of west-central Florida. Mar. Geol. 200, 351–378. doi: 10.1016/s0025-3227(03)00191-9
Lorenzo-Trueba, J., and Ashton, A. D. (2014). Rollover, drowning, and discontinuous retreat: distinct modes of barrier response to sea-level rise arising from a simple morphodynamic model. J. Geophys. Res. 119, 779–801. doi: 10.1002/2013jf002941
McNamara, D. E., and Lazarus, E. D. (2018). “Barrier islands as coupled human–landscape systems,” in Barrier Dynamics and Response to Changing Climate, eds L. J. Moore, and A. B. Murray (Cham: Springer), 363–383. doi: 10.1007/978-3-319-68086-6_12
Mellett, C. L., Hodgson, D. M., Lang, A., Mauz, B., Selby, I., and Plater, A. J. (2012a). Preservation of a drowned gravel barrier complex: a landscape evolution study from the north-eastern English Channel. Mar. Geol. 315, 115–131. doi: 10.1016/j.margeo.2012.04.008
Mellett, C. L., Mauz, B., Plater, A. J., Hodgson, D. M., and Lang, A. (2012b). Optical dating of drowned landscapes: a case study from the English Channel. Quat. Geochronol. 10, 201–208. doi: 10.1016/j.quageo.2012.03.012
Mellett, C. L., and Plater, A. J. (2018). “Drowned barriers as archives of coastal-response to sea-level rise,” in Barrier Dynamics and Response to Changing Climate, eds L. J. Moore, and A. B. Murray (Cham: Springer), 57–89. doi: 10.1007/978-3-319-68086-6_2
Miselis, J. L., and Lorenzo-Trueba, J. (2017). Natural and human-induced variability in barrier-island response to sea level rise. Geophys. Res. Lett. 44, 11922–11931.
Moore, L. J., List, J. H., Williams, S. J., and Stolper, D. (2010). Complexities in barrier island response to sea level rise: insights from numerical model experiments, North Carolina Outer Banks. J. Geophys. Res. 115:F03004.
Mulhern, J. S., Johnson, C. L., and Martin, J. M. (2019). Modern to ancient barrier island dimensional comparisons: implications for analog selection and paleomorphodynamics. Front. Earth Sci. 7:109. doi: 10.3389/feart.2019.00109
Nordfjord, S., Goff, J. A., Austin, J. A. Jr., and Duncan, L. S. (2009). Shallow stratigraphy and complex transgressive ravinement on the New Jersey middle and outer continental shelf. Mar. Geol. 266, 232–243. doi: 10.1016/j.margeo.2009.08.010
Ortiz, A. C., and Ashton, A. D. (2016). Exploring shoreface dynamics and a mechanistic explanation for a morphodynamic depth of closure. J. Geophys. Res. 121, 442–464. doi: 10.1002/2015jf003699
Pretorius, L., Green, A., and Cooper, A. (2016). Submerged shoreline preservation and ravinement during rapid postglacial sea-level rise and subsequent “slowstand”. Bulletin 128, 1059–1069. doi: 10.1130/b31381.1
Rampino, M. R., and Sanders, J. E. (1980). Holocene transgression in south-central Long Island, New York. J. Sediment. Res. 50, 1063–1079.
Rampino, M. R., and Sanders, J. E. (1981). Evolution of the barrier islands of southern Long Island, New York. Sedimentology 28, 37–47. doi: 10.1111/j.1365-3091.1981.tb01661.x
Rampino, M. R., and Sanders, J. E. (1982). Holocene transgression in south-central Long Island, New York: reply. J. Sediment. Res. 52, 1020–1025.
Rampino, M. R., and Sanders, J. E. (1983). Barrier island evolution in response to sea-level rise: reply. J. Sediment. Res. 53, 1031–1033.
Rodriguez, A. B., Anderson, J. B., Siringan, F. P., and Taviani, M. (2004). Holocene evolution of the east Texas coast and inner continental shelf: along-strike variability in coastal retreat rates. J. Sediment. Res. 74, 405–421. doi: 10.1306/092403740405
Salzmann, L., Green, A., and Cooper, J. A. G. (2013). Submerged barrier shoreline sequences on a high energy, steep and narrow shelf. Mar. Geol. 346, 366–374. doi: 10.1016/j.margeo.2013.10.003
Scileppi, E., and Donnelly, J. P. (2007). Sedimentary evidence of hurricane strikes in western Long Island, New York. Geochem. Geophys. Geosyst. 8:Q06011.
Stolper, D., List, J. H., and Thieler, E. R. (2005). Simulating the evolution of coastal morphology and stratigraphy with a new morphological-behaviour model (GEOMBEST). Mar. Geol. 218, 17–36. doi: 10.1016/j.margeo.2005.02.019
Storms, J. E., Weltje, G. J., Terra, G. J., Cattaneo, A., and Trincardi, F. (2008). Coastal dynamics under conditions of rapid sea-level rise: late pleistocene to early holocene evolution of barrier–lagoon systems on the northern Adriatic shelf (Italy). Quat. Sci. Rev. 27, 1107–1123. doi: 10.1016/j.quascirev.2008.02.009
Swift, D. J. (1975). Barrier-island genesis: evidence from the central Atlantic shelf, eastern USA. Sediment. Geol. 14, 1–43. doi: 10.1016/0037-0738(75)90015-9
Keywords: barrier island, autogenic, modeling, sea level, Holocene, meltwater pulse, overstepping
Citation: Ciarletta DJ, Lorenzo-Trueba J and Ashton AD (2019) Interaction of Sea-Level Pulses With Periodically Retreating Barrier Islands. Front. Earth Sci. 7:279. doi: 10.3389/feart.2019.00279
Received: 15 July 2019; Accepted: 17 October 2019;
Published: 31 October 2019.
Edited by:
Brian W. Romans, Virginia Polytechnic Institute and State University, United StatesReviewed by:
Alexander Ray Simms, University of California, Santa Barbara, United StatesMehrdad Sardar Abadi, The University of Oklahoma, United States
Cari Johnson, The University of Utah, United States
Copyright © 2019 Ciarletta, Lorenzo-Trueba and Ashton. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniel J. Ciarletta, Y2lhcmxldHRhZDFAbW9udGNsYWlyLmVkdQ==
 Daniel J. Ciarletta
Daniel J. Ciarletta Jorge Lorenzo-Trueba
Jorge Lorenzo-Trueba Andrew D. Ashton
Andrew D. Ashton