
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Big Data , 16 October 2020
Sec. Data Mining and Management
Volume 3 - 2020 | https://doi.org/10.3389/fdata.2020.00030
This article is part of the Research Topic Big Spatial Data View all 5 articles
Due to the ubiquity of spatial data applications and the large amounts of spatial data that these applications generate and process, there is a pressing need for scalable spatial query processing. In this paper, we present new techniques for spatial query processing and optimization in an in-memory and distributed setup to address scalability. More specifically, we introduce new techniques for handling query skew that commonly happens in practice, and minimizes communication costs accordingly. We propose a distributed query scheduler that uses a new cost model to minimize the cost of spatial query processing. The scheduler generates query execution plans that minimize the effect of query skew. The query scheduler utilizes new spatial indexing techniques based on bitmap filters to forward queries to the appropriate local nodes. Each local computation node is responsible for optimizing and selecting its best local query execution plan based on the indexes and the nature of the spatial queries in that node. All the proposed spatial query processing and optimization techniques are prototyped inside Spark, a distributed memory-based computation system. Our prototype system is termed LocationSpark. The experimental study is based on real datasets and demonstrates that LocationSpark can enhance distributed spatial query processing by up to an order of magnitude over existing in-memory and distributed spatial systems.
Spatial computing is becoming increasingly important with the proliferation of mobile devices. Besides, the growing scale and importance of location data have driven the development of numerous specialized spatial data processing systems, e.g., SpatialHadoop (Eldawy and Mokbel, 2015), Hadoop-GIS (Aji et al., 2013). By taking advantage of the power and cost-effectiveness of MapReduce, these systems typically outperform spatial extensions on top of relational database systems by orders of magnitude (Aji et al., 2013). MapReduce-based systems allow users to run spatial queries using predefined high-level spatial operators without worrying about fault tolerance or computation distribution. However, these systems have the following two main limitations: (1) They do not leverage the power of distributed memory, and (2) They are unable to reuse intermediate data (Zaharia, 2016). Nonetheless, data reuse is very common in the spatial data processing. Spatial datasets, e.g., Open Street Map (OSM, for short, >60 G) and Point of Interest
(POI, for short, >20 G) (Eldawy and Mokbel, 2015), are relatively large in size. It is unnecessary to read these datasets continuously from disk [e.g., using HDFS; Shvachko et al., 2010] to respond to user queries. Moreover, intermediate query results have to be written back to HDFS, thus directly impeding the performance of further data analysis steps.
One way to address the above challenges is to develop an efficient execution engine for large-scale spatial data computation based on a memory-based computation framework (in this case, Spark; Zaharia, 2016). Spark is a computation framework that allows users to work on distributed in-memory data without worrying about data distribution or fault-tolerance. Recently, various Spark-based systems have been proposed for spatial data analysis, e.g., GeoSpark (Yu et al., 2015), Simba (Xie et al., 2016), and LocationSpark (Tang et al., 2016).
Although addressing several challenges in spatial query processing, none of the existing systems can overcome the computation skew introduced by spatial queries. “Spatial query skew” is observed in distributed environments during spatial query processing when certain data partitions are overloaded by spatial queries. Traditionally, distributed spatial computing systems (e.g., Aji et al., 2013; Eldawy and Mokbel, 2015) first, learn the spatial data distribution by sampling the input data. Afterward, spatial data is partitioned evenly into equal-size partitions. For example, in Figure 1, the data points with dark dots are distributed evenly into four partitions. However, the query workload is what may cause computation skew. Given the partitioned data, consider two spatial join operators, namely range and kNN joins, that combine two datasets, say D and Q, with respect to a spatial relationship. For each point q ∈ Q, a spatial range join [Figure 1 (left)] returns data points in D that are inside the circle centered at q. In contrast, a kNN join [Figure 1 (right)] returns the k nearest-neighbors from the dataset D for each query point q ∈ Q. Both spatial operators are expensive, and may incur computation skew in certain workers, thus greatly degrading the overall performance.
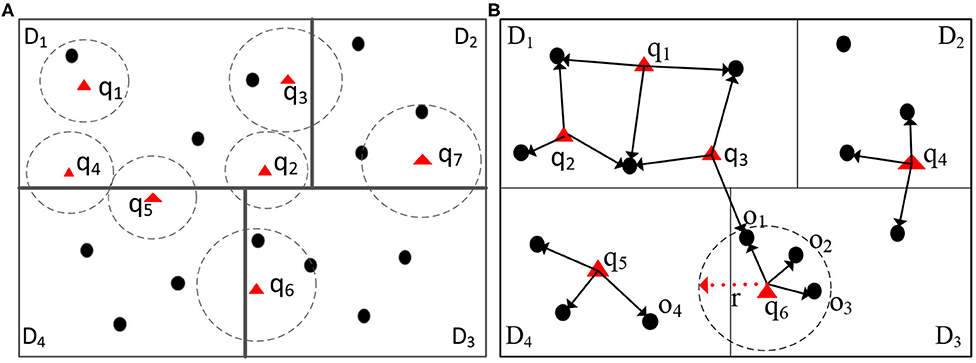
Figure 1. Illustration of spatial join and kNN join operators. Circles centered around the triangle focal points form one dataset, and the black dots form the second dataset. Spatial range join returns (dot, triangle) pairs when the dot is inside the circle. kNN join returns (triangle, dot) pairs when the dot is among the three nearest dots to the triangle. (A) Range join, (B) 3NN join.
For illustration, consider a large spatial dataset, with millions of points of interests (POIs), that is partitioned into different computation nodes based on the spatial distribution of the data, e.g., one data partition represents data from San Francisco, CA, and another represents data from Chicago, IL. Assume that we have incoming queries from people looking for different POIs, e.g., restaurants, train, or bus stations, and grocery stores, around their locations. These spatial range queries are consolidated into batches to be joined via an index on the POI data (e.g., using indexed nested-loops join). After partitioning the incoming spatial queries based on their locations, we observe the following issues: During rush hours in San Francisco from 4 p.m. to 6 p.m. (PST), San Francisco's data partition may encounter more queries than the data partition in Chicago, since it is already evening time in Chicago. Without an appropriate optimization technique, the data partition for San Francisco will take much longer time to process its corresponding queries while the workers responsible for the Chicago partition is lightly loaded. Similarly, if in Figure 1, the data points (the dark dots) correspond to the GPS records of Uber's cars, where multiple users (the triangles) are looking for the Uber carpool service around them. Partition D1, that corresponds, say to an airport, experiences more queries than the other partitions because people may prefer using Uber at this location. Being aware of the spatial query skew provides a new opportunity to optimize queries in distributed spatial data environments. The skewed partitions have to be assigned more computation power to reduce the overall processing time.
Furthermore, communication cost, generally a key factor of the overall performance, may become a bottleneck. When a spatial query touches more than one data partition, it may be the case that some of these partitions do not contribute to the final query result. For example, in Figure 1 (left part), queries q2, q3, q4, and q5 overlap more than one data partition (D1, D2, and D4). Traditionally, system would think these partitions would contribute the final query results, however, these partitions do not contain data points that satisfy the queries, since these queries overlap partitions only. Thus, scheduling queries (e.g., q4 and q5) to the overlapping data partition D4 incurs unnecessary communication costs. More importantly, for the spatial range join or kNN join operators over two large datasets, the cost of the network communication may become prohibitive without proper optimization.
In this paper, we introduce LOCATIONSPARK, an efficient memory-based distributed spatial query processing system. LOCATIONSPARK has a query scheduler to mitigate query skew. The query scheduler uses a cost model to analyze the skew for use by the spatial operators, and a plan generation algorithm to construct a load-balanced query execution plan. After plan generation, local computation nodes select the proper algorithms to improve their local performance based on the available spatial indexes and the registered queries on each node. Finally, to reduce communication cost when dispatching queries to their overlapping data partitions, LOCATIONSPARK adopts a new spatial bitmap filter, termed sFilter, that can speed up query processing by avoiding needless communication with data partitions that do not contribute to the query answer. We implement LOCATIONSPARK as a library in Spark that provides an API for spatial query processing and optimization based on Spark's standard dataflow operators.
The main contributions of this paper is as follows:
1. We present LOCATIONSPARK, a spatial computing system for the efficient processing of spatial queries in a distributed in-memory environment.
2. We address data and query skew issues to improve load balancing while executing spatial operators, e.g., spatial range joins and kNN joins. LOCATIONSPARK produces cost-optimized query execution plans over in-memory distributed spatial data.
3. We introduce a new lightweight yet efficient spatial bitmap filter to reduce communication costs.
4. We realize the introduced query processing and optimization techniques inside LOCATIONSPARK, and conduct a large-scale evaluation on real spatial data and common benchmark algorithms. We compare LOCATIONSPARK against state-of-the-art distributed spatial data processing systems. Experimental results illustrate an enhancement in performance by up to an order of magnitude over existing in-memory distributed spatial query processing systems.
The rest of this paper proceeds as follows. Section 2 presents the problem definition and an overview of distributed spatial query processing. Section 3 introduces the cost model and the cost-based query plan scheduler and optimizer and their corresponding algorithms. Section 4 presents an empirical study for local execution plans in local computation nodes. Section 5 introduces the spatial bitmap filter, and explains how it can speedup spatial query processing in a distributed setup. The experimental results are presented in section 6. Section 7 discusses the related work. Finally, section 8 concludes the paper.
LOCATIONSPARK stores spatial data as key-value pairs. A tuple, say oi, contains a spatial geometric key ki and a related value vi. The spatial data type for key ki can be a two-dimensional point, e.g., latitude-longitude, a line-segment, a poly-line, a rectangle, or a polygon. The value types vi is specified by the user, e.g., a text data type if the data tuple is a tweet. In this paper, we assume that queries are issued continuously by users, and are processed by the system in batches (e.g., similar to the DStream model; Zaharia, 2016).
LOCATIONSPARK supports various types of spatial query predicates including spatial range search, k-NN search, spatial range join, and kNN join. In this paper, we focus our discussion on the spatial range join and kNN join operators on two datasets, say Q and D, the form the outer and inner tables, respectively.
Definition 1. Spatial Range Select—range(q,D): Given a spatial range area q (e.g., circle or rectangle) and a dataset D, range(q,D) finds all tuples from D that overlap the spatial range de fined by q.
Definition 2. Spatial Range Join—Q⋈sjD: Given two datasets Q and D, Q⋈sjD, combines each object q ∈ Q with its range search results from D, Q⋈sjD= {(q, o)|q ∈ Q, o ∈ range(q,D)}.
Definition 3. kNN Select—kNN(q,D): Given a query tuple q, a dataset D, and an integer k, kNN(q,D), returns the output set {o|o ∈ D and ∀s ∈ D and s≠o, ||o, q|| ≤ ||s, q||}, where the number of output objects from D, |kNN(q,D)| = k.
Definition 4. kNN Join—Q⋈knnD: Given a parameter k, kNN join of Q and D computes for each object q ∈ Q its k-nearest-neighbors in D. Q⋈knnD= {(q, o)|∀q ∈ Q, ∀o ∈ kNN(q,D)}.
To facilitate spatial query processing, in LOCATIONSPARK, we construct a distributed spatial index for in-memory spatial data. Given a spatial dataset D, we obtain samples from D, and construct over these samples a spatial index (e.g., an R-tree) with N leaves. We refer to this index on the sample data as the global spatial index. It partitions D via data shuffling into N partitions. The global spatial index guarantees that each data partition approximately has the same amount of data. Then, each worker Wi of the N workers has a local data partition Di that is roughly 1/Nth of the data and constructs a local spatial index. Finally, the indexed data (termed the LocationRDD) is cached into memory. Figure 2 gives the architecture of LOCATIONSPARK and the physical representation of the partitioned spatial data based on the procedure outlined above, where the master node (e.g., Master in the Figure) stores the global spatial index that indexes the data partitions, while each worker has a local spatial index (e.g., the black triangle in the Figure) over the local spatial data within the partition. Notice that the global spatial index partitions the data into LocationRDDs as in Figure 2, and this index can be copied into various workers to help partition the data in parallel. The type of each local index, e.g., a Grid, an R-tree, or an IR-tree, for a data partition can be determined based on the specifics of the application scenarios. For example, a Grid can be used for indexing moving objects while an R-tree can be used for polygonal objects. For spatial range join, two strategies are possible; either replicate the outer table and send it to the node where the inner table is, or replicate the inner table data and send it to the different processing nodes where the outer table tuples are. In a shared execution, the outer table is typically a collection of range query tuples, and the inner table is the queried dataset. If this is the case, it would make more sense to send the outer table of queries to the inner data tables as the outer table is usually much smaller compared to the inner data tables. In this paper, we adopt this technique because it would be impracticable to replicate and forward copies of the large inner data table.
Thus, each tuple q ∈ Q is replicated and forwarded to the partitions that spatially overlap with it. These overlapping partitions are identified using the global index. Then, a post-processing step merges the local results to produce the final output. For example, we replicate q2 in Figure 1 (left part) and forward it to data partitions D1, D3, and D4. Then, we execute a spatial range search on each data partition locally. Next, we merge the local results to form the overall output of tuple q2. As illustrated in Figure 2, the outer table that corresponds to a shared execution plan's collection of queries (termed queryRDD) are first partitioned into qRDD based on the overlap between the queries in qRDD and the corresponding data partitions. Then, the local search takes place over the local data partitions of LocationRDD.
The kNN join operator is implemented similarly in a simple two-round process. First, each outer focal point qi ∈ Q is transferred to the worker that holds the data partition that qi spatially belongs to. Then, the kNN join is executed locally in each data partition, producing the kNN candidates for each focal point qi. Afterward, the maximum distance from qi to its kNN candidates, say radius ri, is computed. If the radius ri overlaps multiple data partitions, Point qi is replicated into these overlapping partitions, and another set of kNN candidates is computed in each of these partitions. Finally, we merge the kNN candidates from the various partitions to get the exact result. For example, in Figure 1 (right), assume that we want to evaluate a 3NN query for Point q6. The first step is to find the 3NN candidates for q6 in data Partition D3. Next, we find that the radius r for the 3NN candidates from Partition D3 overlaps Partition D4. Thus, we need to compute the 3NN of q6 in Partition D4 as well. Notice that the radius r can enhance the 3NN search in Partition D4 because only the data points within Radius r are among the 3NN of q6. Finally, the 3NN of q6 are o1, o2, and o3.
The outer and inner tables (or, in shared execution terminology, the queries, and the data) are spatially collocated in distributed spatial query processing. We refer to the outer table as being the queries table, e.g., containing the ranges of range operations, or the focal points of kNN operations. Assume further that the outer (queries) table is the smaller of the two. We refer to the inner table by the data table (in the case of shared execution of multiple queries together). The distribution of the incoming spatial queries (in the outer tables) changes dynamically over time, with bursts in certain spatial regions. Thus, evenly distributing the input data D to the various workers may result in a load imbalance at times. LOCATIONSPARK's scheduler identifies the skewed data partitions based on a cost model, repartitions, and redistributes the data accordingly, and selects the optimal repartitioning strategies for both the outer and inner tables, and consequently generates an overall optimized execution plan.
Communication cost is a major factor that affects system performance. LOCATIONSPARK adopts a spatial bitmap filter to reduce network communication costs. The role of the spatial bitmap filter is to prune the data partitions that overlap the spatial ranges from the outer tables but do not contribute to the final operation's results. This spatial bitmap filter is memory-based and is space- and time-efficient. The spatial bitmap filter adapts its structure as the data and query distributions change.
This section addresses how to dynamically handle query skew (the outer table of the join). First, we present the cost functions for query processing and analyze the bottlenecks. Then, we show how to repartition the skewed data partitions to speed up processing. This is formulated as an optimization problem that we show is NP-complete. Consequently, we introduce an approximation algorithm to solve the data skew repartitioning problem. Although presented for spatial range joins, the proposed technique all applies to kNN joins.
The inner table D of the spatial range join is distributed into N data partitions, where each partition Di is indexed and is cached in memory. For the query table Q (i.e., the outer table of spatial range join), each query qi ∈ Q is shuffled to the data partitions that spatially overlap with it. Let ϵ(Q, N) be the shuffling cost, and E(Di) be the execution time of local queries at Partition Di. The execution times of local queries depend on the queries and the built indexes. The estimation of E(Di) is presented later. After the local results are computed, the post-processing step merges the local results to produce the final output. The corresponding cost is denoted by ρ(Q).
Overall, the runtime cost for the spatial range join operation is:
where N is the number of data partitions. In reality, the cost of query shuffling is far less than the other costs as the number of queries is much smaller than the number of data items. Thus, the runtime cost can be estimated as follows:
We categorize the data partitions into two types: skewed (Ds) and non-skewed (Dns). The execution time of the local queries in the skewed partitions is the bottleneck. The runtime costs for skewed and non-skewed data partitions are and , respectively, where (and ) is the number of skewed (and non-skewed) data partitions, and . Thus, Equation (2) can be rewritten as follows:
The goal of the query scheduler is to minimize the query processing time subject to the following constraints: (1) The limited number of available resources (i.e., the number of partitions) in a cluster, and (2) The overhead of network bandwidth and disk I/O. Given the partitioned and indexed spatial data, the cost estimators for query processing based on sampling (that is introduced below), and the available number of data partitions, the optimizer returns an execution plan that minimizes query processing time. First, the optimizer determines if any partitions are skewed. Then, it repartitions them subject to the introduced cluster and networking constraints. Finally, the optimizer evaluates the plan on the newly repartitioned data to determine whether or not it minimizes query execution time (see Figure 3). For example, the partition D is repartitioned into two parts for skew issues.
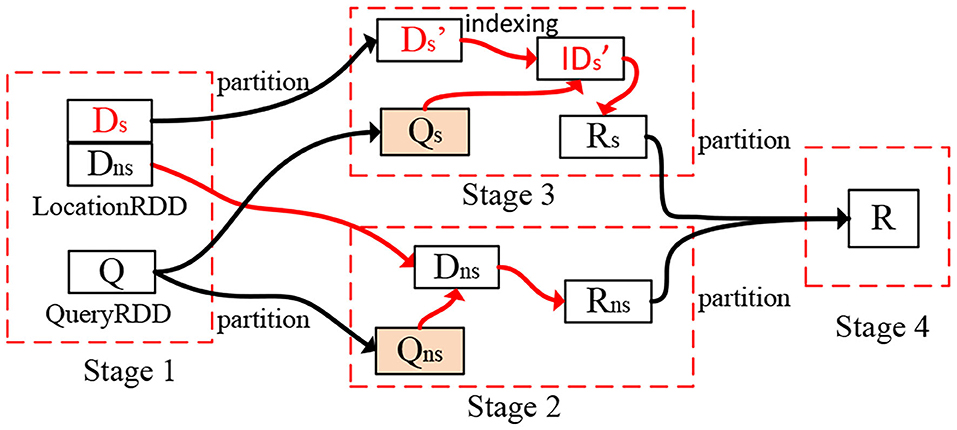
Figure 3. Execution plan for spatial range join. The red lines identify local operations, and black lines show the data partitioning.
Estimating the runtime cost of executing the local queries and the cost of merging the final results is not straightforward. The local query processing time E(Di) is influenced by various factors including the types of spatial indexes used, the number of data points in Di, the number of queries directed to Di, related spatial regions, and the available memory. Similar to Kwon et al. (2010), we assume that the related cost functions are monotonic, and can be approximated using samples from the outer and inner tables (queries and data). Thus, the local query execution time is formulated as follows: , where is a sample of the original inner table dataset, is the sample of the outer table queries, A is the area of the underlying spatial region, and α is the sample ratio to scale up the estimate to the entire dataset. After computing a representative sample of the data points and queries, e.g., using reservoir sampling (Vitter, 1985), the cost function E(Di) estimates the query processing runtime in Data Partition Di. More details on computing E(Di), ρ(Qi), and the sample size can be found in Kwon et al. (2010).
Given the estimated runtime cost over skewed and non-skewed partitions, the optimizer splits one skewed data Partition into m′ data sub-partitions. Assume that is the set of queries originally assigned to Partition . Let the overheads due to data shuffling, re-indexing, and merging be , , and , respectively. After splitting a skewed partition (), the new runtime is:
Hence, we can split into multiple partitions only if . As a result, the new query execution time is:
Thus, we can formulate the query plan generation based on the data repartitioning problem as follows:
Definition 5. Let D be the set of spatially indexed data partitions, Q be the set of spatial queries, M be the total number of data partitions, and their corresponding cost estimation functions, i.e., local query execution E(Di), data repartitioning β(Di), and data indexing cost estimates γ(Qi). The query optimization problem is to choose a skewed Partition Ds from D, repartition each into multiple partitions, and assign spatial queries to the new data partitions. The new data partition set, say D′, contains partitions . s.t. (1) and (2) |D′| ≤ M.
Unfortunately, as we show below, this problem is NP-complete. In the next section, we present a greedy algorithm for this problem.
Theorem 1. Optimized query plan generation with data repartitioning for distributed indexed spatial data is NP-complete.
The proof is given in Mingjie et al. (2016).
The general idea is to search for skewed partitions based on their local query execution times. Then, we split the selected data partitions only if the runtime can be improved. If the runtime cannot be improved, or if all the available data partitions are consumed, then the algorithm terminates. While this greedy algorithm cannot guarantee optimal query performance, our experiments show significant improvement (by one order of magnitude) over the plan executing on the original partitions. Algorithm 1 gives the pseudocode for the greedy partitioning procedure.

Algorithm 1 includes two functions, namely numberOfPartitions and repartition. Function numberOfPartitions in line 7 computes the number of sub-partitions m′ that the skewed partition will be split into. We could split a skewed partition into two partitions each time, but this is not necessarily efficient. Given data partitions D = {D1, D2, …, DN}, let Partition D1 be the one with the largest local query execution time E(D1). From Equation (2), the execution time is approximated by E(D1)+ρ(Q). To reduce this execution time, D1 is split into m′ partitions, and the query execution time for D1 is updated to . For all other partitions Di ∈ D (i≠1), the runtime is the , where i = [2, …, N] and Q′ are the queries related to all data partitions except D1. Thus, the runtime is , and is improved if
As a result, we need to compute the minimum value of m′ to satisfy Equation (6), since Δ, E(D1), and ρ(Q) are known.
Function repartition in line 8 splits the skewed data partitions and reassigns the spatial queries to the new data partitions using two strategies. The first strategy repartitions based on data distribution. Because each data partition Di is already indexed by a spatial index, the data distribution can be learned directly by recording the number of data points in each branch of the index. Then, we repartition data points in Di into multiple parts based on the recorded numbers while guaranteeing that each newly generated sub-partition contains an equal amount of data. In the second strategy, we repartition a skewed Partition Di based on the distribution of the spatial queries. First, we collect a sample Qs from the queries Qi that are originally assigned to Partition Di. Then, we compute how Qs is distributed in Partition Di by recording the frequencies of the queries as they belong to branches of the index over the data. Thus, we can repartition the indexed data based on the query frequencies. Although the data sizes may not be equal, the execution workload will be balanced. In our experiments, we choose this second approach to overcome query skew. To illustrate how the proposed query-plan optimization algorithm works, consider the following example.
Running Example. Given data partitions D = {D1, D2, D3, D4, D5}, where the number of data points in each partition is 50, the number of queries in each partition Di, 1 ≤ i ≤ 5 is 30, 20, 10, 10, and 10, respectively, and the available data partitions M is 5. For simplicity, the local query processing cost is E(Di) = |Di| × |Qi| × pe, where pe = 0.2 is a constant. The cost of merging the results is ρ(Q) = |Q| × λ × pm, where pm = 0.05, and λ = 10 is the approximate number of retrieved data points per query. The cost of data shuffling and re-indexing after repartitioning is , and γ(Ds) = |Ds| × px, respectively, where pr = 0.01 and px = 0.02. Without any optimization, from Equation (2), the estimated runtime cost for this input table is 340. LOCATIONSPARK optimizes the workload as follows. At first, it chooses Data Partition D1 as the skewed partition to be repartitioned because D1 has the highest local runtime (300), while the second largest cost is D2's (200). Using Equation (6), we split D1 into two partitions, i.e., m′ = 2. Thus, Function repartition splits D1 into the two partitions and based on the distribution of queries within D1. The number of data points in and is 22 and 28, respectively, and the number of queries are 12 and 18, respectively. Therefore, the new runtime is reduced to ≈200+25 because D1's runtime is reduced to ≈100 based on Equation (4). Therefore, the two new data partitions and are introduced in place of D1. Next, Partition D2 is chosen to be split into two partitions, and the optimized runtime becomes ≈100+15. Finally, the procedure terminates as only one available partition is left.
Once the query plan is generated, each computation node chooses a specific local execution plan based on the queries assigned to it and the indexes it has. We implement various centralized algorithms for spatial range join and kNN join operators within each worker and study their performance. The algorithms are implemented in Spark. We use the execution time as the performance measure.
We implement two algorithms for spatial range join (Sowell et al., 2013). The first is indexed nested-loops join, where we probe the spatial index repeatedly for each outer tuple (or range query in the case of shared execution). The tested algorithms are nestRtree, nestGrid, and nestQtree, where they use an R-tree, a Grid, and a Quadtree as an index for the inner table, respectively. The second algorithm is based on the dual-tree traversal (Brinkhoff et al., 1993). It builds two spatial indexes (e.g., an R-tree) over both the input queries and the data, and performs a depth-first search over the dual trees simultaneously.
Similar to the spatial range join, indexed nested-loops can be applied to kNN join, where it computes the set of kNN objects for each query point in the outer table. An index is built on the inner table (the data table). The other kinds of kNN join algorithms are block-based. They partition the queries (the outer table) and the data points (the inner table) into different blocks and find the kNN candidates for queries in the same block. Then, post-processing refines step computes kNN for each query point in the same block. Gorder (Xia et al., 2004) divides query and data points into different rectangles based on the G-order, and utilizes two distance bounds to reduce the processing of unnecessary blocks. For example, the min-distance bound is the minimum distance between the rectangles of the query points and the data points. The max-distance bound is the maximum distance from the queries to their kNN sets. If the max-distance is smaller than the min-distance bound, the related data block is pruned. PGBJ (Lu et al., 2012) has a similar idea that extends to parallel kNN join using MapReduce.
Recently, Spitfire (Chatzimilioudis et al., 2016) is a parallel kNN self-join algorithm for in-memory data. It replicates the possible kNN candidates into its neighboring data blocks. Both PGBJ and Spitfire are designed for parallel kNN join, but they are not directly applicable to indexed data. The reason is that PGBJ partitions queries and data points based on the selected pivots while Spitfire is specifically optimized for kNN self-join.
LOCATIONSPARK enhances the performance of the local kNN join procedure. For Gorder (Xia et al., 2004), instead of using the expensive principal component analysis (PCA) in Gorder, we apply the Hilbert curve to partition the query points. We term the modified Gorder method sfcurve. We modify PGBJ as follows. First, we compute the pivots of the query points based on a clustering algorithm (e.g., k-means) oversample data, and then partition the query points into different blocks based on the computed pivots. Next, we compute the MBR of each block. Because the data points are already indexed (e.g., using an R-tree), the min-distance from the MBRs of the query points and the index data is computed, and the max-distance bound is calculated based on the kNN results from the pivots. This approach is termed pgbjk. For Spitfire, we use a spatial index to speed up finding the kNN candidates.
In this section, we introduce a new spatial bitmap filter termed sFilter. The sFilter helps us decide for an outer tuple, say q, in a spatial range join, if there exist tuples in the inner table that join with q. This helps reduce the communication overhead. For example, consider an outer tuple q of a spatial range join where q has a range that overlaps multiple data partitions of the inner table. Typically, all the overlapping partitions need to be examined by communicating q's range to them and searching the data within each partition to test for overlap with q's range. This incurs high communication and search costs. Using the sFilter, given q's range that overlaps multiple partitions of the inner table, the sFilter can decide which overlapping partitions contain data that overlaps q's range without actually communicating with and searching the data in the partitions. Only the partitions that contain data that overlap q's range are the ones that will be searched.
Figure 4 gives an example sFilter. Conceptually, an sFilter is a new in-memory variant of a quadtree that has internal and leaf nodes (Samet, 2005). Internal nodes are for index navigation, and leaf nodes, each has a marker to indicate whether or not there are data items in the node's corresponding region. We encode the sFilter into two binary codes and execute queries over this encoding.
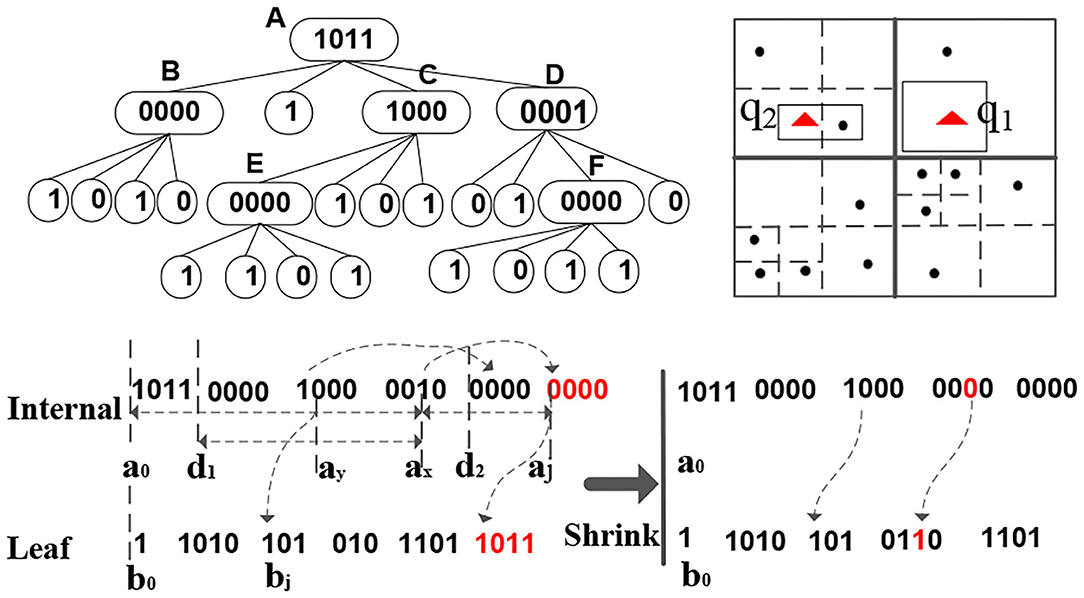
Figure 4. sFilter structure (up left), the related data (up right), and the two bit sequences of the sFilter (down).
The sFilter is encoded into two long sequences of bits. The first bit-sequence corresponds to internal nodes while the second bit-sequence corresponds to leaf nodes. Notice that in these two binary sequences, no pointers are needed. Each internal node of the sFilter takes four bits, where each bit represents one of the internal node's children. These children are encoded in clockwise order starting from the upper-left corner. Each bit value of an internal node determines the type of its corresponding child, i.e., whether the child is internal (a 1 bit) or leaf (a 0 bit). In Figure 4, the root (internal) node A has binary code 1011, i.e., it has three of its children being internal nodes, and its second node is a leaf node. The four-bit encodings of all the internal nodes are concatenated to form the internal-node bit-sequence of the sFilter. The ordering of the internal nodes in this sequence is based on a breadth-first search (BFS) traversal of the quadtree. In contrast, a leaf node only takes one bit, and its bit value indicates whether or not data points exist inside the spatial quadrant corresponding to the leaf. In Figure 4, Internal Node B has four children, and the bit values for B's leaf nodes are 1010, i.e., the first and third leaf nodes of B contain data items. During the BFS on the underlying quad-tree of the sFilter, simultaneously construct the bit-sequences for all the leaf and internal nodes. The sFilter is encoded into the two binary sequences in Figure 4. The space usage of an sFilter is ((4d−1−1)/3) × 4+4d−1 Bits, where (4d−1−1)/3 and 4d−1 are the numbers of internal nodes and leaf nodes, respectively, and d = o(log(L)) is the depth of quadtree and L is the length of the space.
Consider the internal node D in Figure 4. D's binary code is 0001, and the fourth bit has Value 1 at Memory Address ax of the internal-nodes bit-sequence. Thus, this bit refers to D's child F that is also an internal node at Address aj. Because the sFilter has no pointers, we need to compute F's address aj from ax. Observe that the number of bits with Value 1 from Start Address a0 of the binary code to ax can be used to compute the address.
Definition 6 . Let a be the bit sequence that starts at Address a0. χ(a0, ax) and τ(a0, ax) are the number of bits with Values 1 and 0, respectively, from Addresses a0 to ax inclusive.
χ(a0, ax) is the number of internal nodes up to ax. Thus, Address aj of F is (a0+5 × 4) because there are 5 bits with value 1 from a0 to ax. Similarly, if one child node is a leaf node, its address is inferred from τ(a0, ax) as follows:
Proposition 1. Let a and b be the sFilter's bit sequences for internal and leaf nodes in Memory Addresses a0 and b0, respectively. To access a node's child in memory, we need to compute its address. The address, say aj, of the xth child of an internal node at Address ax is computed as follows. If the bit value of ax is 1, then aj = a0+4 × χ(a0, ax). If the bit value of ax is 0, aj = b0+τ(a0, ax).
We adopt the following two optimizations to speedup the computation of χ(a0, ax) and τ(a0, ax): (1) Precomputation and (2) Set counting. Let di be the memory address of the first internal node at Height (or Depth) i of the underlying quadtree when traversed in BFS order. For example, in Figure 4, Nodes B and E are the first internal nodes in BFS order at Depths 1 and 2 of the quadtree, respectively. For all i ≤ depth of the underlying quadtree, we precompute χ(a0, di), e.g., χ(a0, d1) and χ(a0, d2) in Figure 4. Notice that d0 = a0 and χ(a0, d0) = 0. Then, Address aj that corresponds to the memory address of the xth child of an internal node at Address ax can be computed as follows. aj = a0+(χ(a0, d1)+χ(d1, ax)) × 4. χ(a0, d1) is precomputed. Thus, we only need to compute on the fly χ(d1, ax). Furthermore, evaluating χ can be optimized by a bit set counting approach, i.e., a lookup table or a sideways addition1 that can achieve constant-time complexity.
After getting one node's children via Proposition 1, we apply Depth-First Search (DFS) over the binary codes of the internal nodes to answer a spatial range query. The procedure starts from the first four bits of Bit Sequence a, since these four bits are the root node of the sFilter. Then, we check the four quadrants, say rs, of the children of the root node, and iterate over rs to find the quadrants, say , overlapping the input query range qi. Next, we continue searching the children of based on the addresses computed from Proposition 1. This recursive procedure stops if a leaf node is found with Value 1, or if all internal nodes are visited. For example, consider Range Query q2 in Figure 4. We start at Root Node A (with Bit Value 1011). Query q2 is located inside the northwestern (NW) quadrant of A. Because the related bit value for this quadrant is 1, it indicates an internal node type, and it refers to Child Node B. Node B's memory address is computed by a0+1 × 4 because only one non-leaf node (A) is before B. B's related bit value is 0000, i.e., B contains four leaf nodes. The procedure continues until finding one leaf node of B, mainly the southeastern child leaf node, with Value 1 that overlaps the query, and thus returns True.
Since the depth of the sFilter affects query performance, it is impractical to use only one sFilter in a distributed setting. Thus, we embed multiple sFilters into the global and local spatial indexes in LOCATIONSPARK. In the master node, separate sFilters are placed into the different branches of the global index, where the role of each sFilter is to locally answer the query for the specific branch it is in. In the local computation nodes, an sFilter is built, and it adapts its structure based on data updates and changes in query patterns.
Algorithm 2 gives the procedure for performing the spatial range join using the sFilter. Initially, the outer (queries) table is partitioned according to the global index. The global index identifies the overlapping data partitions for each query q. Then, the sFilter tells which partitions contain data that overlap the query range (Line 2 of the algorithm). After performing the spatial range join (Line 14), the master node fetches the updated sFilter from each data worker, and refreshes the existing sFilters in the master node (Lines 15–16). Lines 2–13 update the sFilter of each worker (as in Figure 2).

The sFilter can improve the kNN search and kNN join because they also depend on spatial range search. Moreover, their query results may enhance the sFilter by lowering the false positive errors as illustrated below.
The build and update operations of the sFilter are first executed at the local workers in parallel. Then, the updated sFilters are propagated to the master node.
The initial sFilter is built from a temporary local quadtree (Samet, 2005) in each partition. Then, the sFilter is adapted based on the query results. For example, consider Query q1 in Figure 4. Initially, the sFilter reports that there is data for q1 in the partitions. When q1 visits the related data partitions, it finds that no data points are overlapping q1 in the partitions, i.e., a false-positive (+ve) error. Thus, we mark the quadrants precisely covered by q1 in the sFilter as empty, and hence reduce the false positive errors if queries visit the marked quadrants again. Function insert in Algorithm 2 recursively splits the quadrants covered by the empty query, and marks these generated quadrants as empty. After each local sFilter is updated in each worker, these updates are reflected into the master node. The compact encoding of the sFilter saves the communication cost between the workers and the master.
However, the query performance of the sFilter degrades as the size of the index increases. Function shrink in Algorithm 2 merges some branches of the sFilter at the price of increasing false-positive errors. For example, one can shrink Internal Node F in Figure 4 into a leaf node, and updating its bit value to 1, although one quadrant of F does not contain data. Therefore, we might track the visit frequencies of the internal nodes, and merge internal nodes with low visiting frequency. Then, some well-known data caching policies, e.g., LRU or MRU, can be used. However, the overhead to track the visit frequencies is expensive. In our implementation, we adopt a simple bottom-up approach. We start merging the nodes from the lower levels of the index to the higher levels until the space constraint is met. In Figure 4, we shrink the sFilter from Internal Node F, and replace it by a leaf node, and update its binary code to 1. F's leaf children are removed. The experimental results show that this approach increases the false-positive errors, but enhances the overall query performance.
LOCATIONSPARK is implemented on top of Resilient Distributed Datasets (RDDs); these key components of Spark are fault-tolerant collections of elements that can be operated on in parallel. LOCATIONSPARK is a library of Spark, and provides the Class LocationRDD for spatial operations (Mingjie et al., 2016). Statistics are maintained at the driver program of Spark, and the execution plans are generated at the driver. Local spatial indexes are persisted in the RDD data partitions, while the global index is realized by extending the interface of the RDD data partitioner. The data tuples and related spatial indexes are encapsulated into the RDD data partitions. Thus, Spark's fault tolerance naturally applies to in LOCATIONSPARK. The spatial indexes are immutable and are implemented based on the path copy approaches. Thus, each updated version of the spatial index can be persisted into a disk for fault tolerance. This enables the recovery of a local index from disk in case of failure in a worker. The Spark cluster is managed by YARN, and a failure in the master nodes is detected and managed by ZooKeeper. In the case of a master node failure, the lost master node is evicted and a standby node is chosen to recover the master. As a result, the global index and the sFilter in the master node are recoverable. Finally, the built spatial index data can be stored into a disk, and enables further data analysis without additional data repartitioning or indexing. LOCATIONSPARK is open-source, and can be downloaded from https://github.com/merlintang/SpatialSpark.
Experiments are conducted on two datasets. Twitter: 1.5 Billion Tweets (around 250 GB) are collected over a period of nearly 20 months (from January 2013 to July 2014), and is restricted to the USA spatial region. The format of a tweet is the identifier, timestamp, longitude-latitude coordinates, and text. OSMP: is shared by the authors of SpatialHadoop (Eldawy and Mokbel, 2015). OSMP represents the map features of the whole world, where each spatial object is identified by its coordinates (longitude, latitude) and an object ID. It contains 1.7 Billion points with a total size of 62.3GB. We generate two types of queries. (1) Uniformly distributed (USA, for short): We uniformly sample data points from the corresponding dataset, and generate spatial queries from the samples. These are the default queries in our experiments. (2) Skewed spatial queries: These are synthesized around specific spatial areas, e.g., Chicago, San Francisco, New York (CHI, SF, NY, respectively, for short). The spatial queries and data points are the outer and inner tables Q and D for the experimental studies of the spatial range and kNN joins presented below.
Our study compares LOCATIONSPARK with the following: (1) GeoSpark (Yu et al., 2015) uses ideas from SpatialHadoop, but is implemented over Spark. (2) SpatialSpark (You, 2015) performs partition-based spatial joins. (3) Magellan (Hortonworks, 2015) is developed based on Spark's dataframes to take advantage from Spark SQL's plan optimizer. However, Magellan does not have spatial indexing. (4) State-of-art kNN-join: Since none of the three systems support kNN join, we compare LOCATIONSPARK with a state-of-art kNN-join approach (PGBJ; Lu et al., 2012) that is provided by PGBJ's authors. (5) Simba (Xie et al., 2016) is a spatial computation system based on Spark SQL with spatial distance join and kNN-join operator. We also modified Simba with the developed techniques (e.g., query scheduler and sFilter) inside, the optimized Simba is called Simba(opt). (6) LocationSpark(opt) and LocationSpark refers to the query scheduler and sFilter is applied or not, respectively. We do not compare against Stark (Hagedorn et al., 2017), since GeoSpark shows better performance than Stark in most of the cases.
We use a cluster of six physical nodes Hathi2. that consists of Dell compute nodes with two 8-core Intel E5-2650v2 CPUs, 32 GB of memory, and 48TB of local storage per node. Meanwhile, in order to test the scalability of LOCATIONSPARK, we set up one Hadoop cluster (with Hortonworks data platform 2.5) on the Amazon EC2 with 48 nodes, each node has an Intel Xeon E5-2666 v3 (Haswell) and 8 GB of memory. Spark 1.6.3 is used with YARN cluster resource management. Performance is measured by the average query execution time.
Table 1 summarizes the spatial range select and spatial index build time by the various approaches. For a fair comparison, we cache the indexed data into memory and record the spatial range query processing time. From Table 1, we observe the following: (1) LOCATIONSPARK is 50 times better than Magellan on the query execution time for the two tables, mainly because the global and local spatial indexes of LOCATIONSPARK can avoid visiting unnecessary data partitions. (2) LOCATIONSPARK with different local indexes, e.g., the R-tree and Quadtree, outperforms SpatialSpark. The speedup is around 50 times since SpatialSpark (without index) has to scan all the data partitions. SpatialSpark (with index) stores the global indexes into a disk and finds data partitions by scanning the global index in the disk. This incurs extra I/O overhead. Also, the local index is not utilized during local searching. (3) LOCATIONSPARK is around 10 times faster than GeoSpark in spatial range search execution time because GeoSpark does not utilize the built global indexes and scans all data partitions. (4) The local index with Quadtree for LOCATIONSPARK achieves superior performance over the R-tree index in terms of index construction and query execution time as discussed in section 4. (5) The index build time among the three systems is comparable because they all scan the data points, which is the dominant factor, and then build the index in memory. (6) LOCATIONSPARK achieves 5 times speedup against Simba since sFilter reduces redundant search of data partitions. This is also observed from Simba(opt) (i.e., with sFilter) that can achieve comparable performance with LOCATIONSPARK.
The execution times of the spatial range join are listed in Figure 5. For a fair comparison, the runtime includes the time to initiate the job, build indexes, execute the join query, and save results into HDFS. Note that Simba does not support spatial range join, it only provides the spatial distance join, where each query is a rectangle or circle with the same size. Performance results for Magellan are not shown because it performs a Cartesian product and hence has the worst execution time. Figure 5 presents the results by varying the data sizes of D (the inner table) from 25 to 150 million, while keeping the size of Q (the outer table) to 0.5 million. The execution time of GeoSpark shows a quadratic increase as the data size increases. GeoSpark's running time is almost 3 h when the data size is 150 million, which is extremely slow. SpatialSpark shows similar trends. The reason is that both GeoSpark and SpatialSpark suffer from the following: (1) The spatial skew issue, where some workers process more data and take a longer time to finish. (2) The local execution plans based on the R-tree and the Grid are slow. (3) Query processing accesses data partitions that do not contribute to the final results. LOCATIONSPARK with the optimized query plans and the sFilter outperforms the two other systems by an order of magnitude. Also, we study the effect of the outer table size on performance. Figure 5 give the run time, and demonstrate that LOCATIONSPARK is 10 times faster than the other two systems. From Figure 5, we also observe that Simba outperforms GeoSpark and SpatialSpark more than one order of magnitude. However, Simba suffers from query skew issues and degrades the performance quickly, because Simba duplicates each data point into multiple data partitions if it spatially overlaps the query rectangles. Naturally, the bigger the spatial query rectangle, the more data points to be duplicated. This introduces redundant network and computation costs. Thus, we place the query scheduler and sFilter into the physical execution part of Simba (e.g., modifying the RDKspark). From the experimental results, the performance of Simba is improved dramatically. This also proves that the proposed approaches in this work could be used to improve other in-memory distributed spatial query processing systems.
Performance of kNN select is given in Figure 6. LOCATIONSPARK outperforms GeoSpark by an order of magnitude. GeoSpark broadcasts the query points to each data partition and accesses each data partition to get the kNN set for the query. Then, GeoSpark collects the local results from each partition, then sorts the tuples based on the distance to a query point of kNN. This is prohibitively expensive and results in large execution times. LOCATIONSPARK only searches for data partitions that contribute to the kNN query point based on the global and local spatial indexes and the sFilter. It avoids redundant computations and unnecessary network communication for irrelevant data partitions.
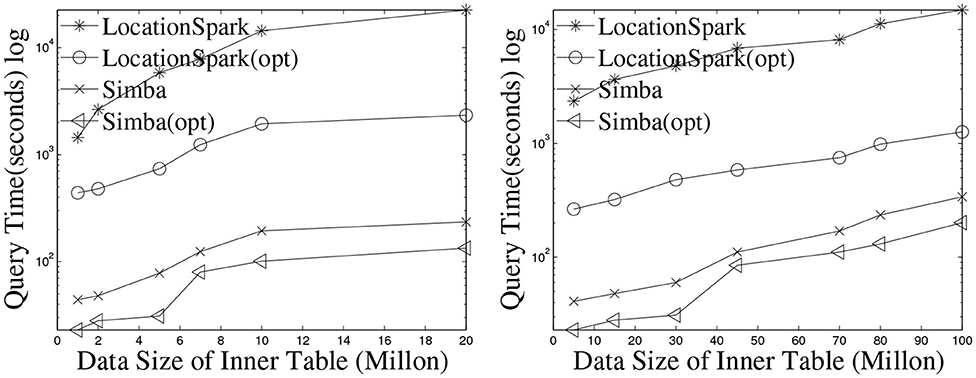
Figure 6. Performance of kNN join by increasing the number of data points for OSMP (left) and Twitter (right).
For kNN join, Figure 7 gives the performance results when varying k on Twitter and OSMP datasets. In terms of runtime, LOCATIONSPARK with optimized query plans and with the sFilter always perform the best. LOCATIONSPARK without any optimizations gives better performance than that of PGBJ. The reason is due to having in-memory computations and avoiding expensive disk I/O when compared to MapReduce jobs. Furthermore, LOCATIONSPARK with optimization shows around 10 times speedup over PGBJ, because the optimized plan migrates and splits the skewed query regions.
We test the performance of the kNN join operator when increasing the number of data points while having the number of queries fixed to 1 million around the Chicago area. The results are illustrated in Figure 8. Observe that LOCATIONSPARK with optimizations performs an order of magnitude better than the basic approach. The reason is that the optimized query plan identifies and repartitions the skewed partitions. In this experiment, the top five slowest tasks in LOCATIONSPARK without optimization take around 33 min, while more than 75% tasks only take <30 s. On the other hand, with an optimized query plan, the top five slowest tasks take <4 min. This directly enhances the execution time.
Observe that Simba outperforms LOCATIONSPARK around 10 times for the kNN join operation. This speedup is achieved by implementing the kNN join via a sampling technique in Simba. More specifically, Simba at first samples query points, and computes the kNN join bound to prune data partitions that do not contribute kNN join results. The computed kNN bound could be very tight when k is small and the query points are well-balanced and distributed. More details can be found in Simba (Xie et al., 2016).
However, the computed kNN join bound has to check for spatial overlap with data points, then duplicate the query points to the overlapping data partitions as well. As a result, Simba would suffer from query skew, where certain data partitions are overwhelmed with query points. Furthermore, a bigger k value introduces redundant network communication because the kNN join bound would be bigger. Similar to spatial join, we place the spatial query scheduler and the sFilter inside the physical execution part of Simba. The query scheduler can detect the skewed data partitions, and the sFilter removes the data partitions that overlap the kNN join bound but has no contributing results. Therefore, the performance of Simba is further improved, e.g., more than three times in this experimental setting.
Furthermore, we study the performance under various query distributions, the number of execution nodes, and the effect of the sFilter. More details are presented in the technical report (Mingjie et al., 2016). In addition, most recent work (Pandey et al., 2018) compare the performance of big spatial data processing system, and it proves LOCATIONSPARK shows much better performance in different aspects.
Spatial data management has been extensively studied for decades and several surveys provide good overviews. Gaede and Günther (1998) provides a good summary of spatial data indexing. Sowell et al. (2013) present a survey and experimental study of iterative spatial-join in memory. Recently, there has been considerable interest in supporting spatial data management over Hadoop MapReduce. Hadoop-GIS (Aji et al., 2013) supports spatial queries in Hadoop by using a uniform grid index. SpatialHadoop (Eldawy and Mokbel, 2015) builds global and local spatial indexes, and modifies the HDFS record reader to read data more efficiently. MD-Hbase (Nishimura et al., 2011) extends HBase to support spatial data update and queries. Hadoop MapReduce is good at data processing for high throughput and fault-tolerance.
Taking advantage of the very large memory pools available in modern machines, Spark and Spark-related systems (e.g., Graphx, Spark-SQL, and DStream) (Gonzalez et al., 2014; Zaharia, 2016) are developed to overcome the drawbacks of MapReduce in specific application domains. To process big spatial data more efficiently, it is natural to develop efficient spatial data management systems based on Spark. Several prototypes have been proposed to support spatial operations over Spark, e.g., GeoSpark (Yu et al., 2015), SpatialSpark (You, 2015), Magellan (Hortonworks, 2015), Simba (Xie et al., 2016), Stark (Hagedorn et al., 2017). However, some important factors impede the performance of these systems, mainly, query skew, lack of adaptivity, and excessive and unoptimized network and I/O communication overheads. For existing spatial join (Brinkhoff et al., 1993; Sowell et al., 2013) and kNN join approaches (Xia et al., 2004; Lu et al., 2012; Chatzimilioudis et al., 2016), we conduct experiments to study their performance in section 4. The reader is referred to section 4. For testing how the proposed techniques to improve Simba, we placed the spatial query scheduler and the sFilter inside Simba standalone version. Simba's standalone version is based on Spark SQL Dataframe while removing the support of the Spark SQL parser. The query scheduler and the sFilter are placed inside the physical plan of Simba (i.e., RDJSpark and RKJSpark). For spatial data updating, it belongs to data processing engine scope but related to data storage like (Memarzia et al., 2019). To support querying over polygonal or polyline objects, we can reuse the spatial index of LOCATIONSPARK (e.g., the local and global indexes), then extend the workload scheduling model and sFilter while considering the properties of polylines. More specifically, a polygon is typically represented by a rectangle that is enclosing the polgyon. The rectangles are used for “filtering.” Anything that is outside the rectangle is guaranteed not to intersect the polygon, Once a query intersects the rectangle, we need to apply a detailed polygon intersection, which is relatively expensive. We can use the sFilter to indicate the empty space between the polygon and its representing rectangle, and this would reduce the computation cost.
Kwon et al. (2010, 2012) proposes a skew handler to address the computation skew in a MapReduce platform. AQWA (Aly et al., 2015) is a disk-based approach that handles spatial computation skew in MapReduce. In LOCATIONSPARK, we overcome the spatial query skew for spatial range join and kNN join operators and provide an optimized query execution plan. These operators are not addressed in AQWA. The query planner in LOCATIONSPARK is different from relational query planners, i.e., join order and selection estimation. ARF (Alexiou et al., 2013) supports a one-dimensional range query filter for data in the disk. Calderoni et al. (2015) study spatial Bloom filter for private data. Yet, it does not support spatial range querying.
We present LOCATIONSPARK, a query executor, and an optimizer based on Spark to improve the query execution plan generated for spatial queries. We introduce a new spatial bitmap filter to reduce the redundant network communication cost. Empirical studies on various real datasets demonstrate the superiority of our approaches compared with existing systems. In the future, we would like to adopt the introduced techniques of LOCATIONSPARK into the Spark SQL optimization engine, and investigate how spatial operations enabled with the spatial bitmap filter would work with relational data operators.
The datasets generated for this study are available on request to the corresponding author.
MT and YY contributed to the design, implementation, and analysis of the results in the manuscript. AM, QM, MO, and WA contributed to the writing of the manuscript. WA also contributed to the design and analysis of the manuscript, in addition to the contribution of writing the manuscript. All authors contributed to the article and approved the submitted version.
YY was employed by the company Facebook. AM was employed by the company Google. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This manuscript has been released as a pre-print at: http://export.arxiv.org/pdf/1907.03736, Tang et al. (2019). Walid G. Aref acknowledges the support of the U.S. National Science Foundation Under Grant Numbers III-1815796 and IIS-1910216. This work was also supported by the Natural Science Foundation of China (Grant No. 61802364).
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fdata.2020.00030/full#supplementary-material
Aji, A., Wang, F., Vo, H., Lee, R., Liu, Q., Zhang, X., et al. (2013). “Hadoop GIS: A high performance spatial data warehousing system over mapreduce,” in VLDB (Trento).
Alexiou, K., Kossmann, D., and Larson, P.-A. (2013). “Adaptive range filters for cold data: avoiding trips to siberia,” in VLDB (Trento).
Aly, A. M., Mahmood, A. R., Hassan, M. S., Aref, W. G., Ouzzani, M., Elmeleegy, H., et al. (2015). “AQWA: adaptive query-workload-aware partitioning of big spatial data,” in VLDB (Kohala Coast, HI).
Brinkhoff, T., Kriegel, H.-P., and Seeger, B. (1993). “Efficient processing of spatial joins using R-trees,” in SIGMOD Rec. (Washington, DC).
Calderoni, L., Palmieri, P., and Maio, D. (2015). Location privacy without mutual trust. Comput. Commun. 68, 4–16. doi: 10.1016/j.comcom.2015.06.011
Chatzimilioudis, G., Costa, C., Zeinalipour-Yazti, D., Lee, W., and Pitoura, E. (2016). “Distributed in-memory processing of all K nearest neighbor queries,” in IEEE Trans. Knowle. Data Eng. 28, 925–938. doi: 10.1109/TKDE.2015.2503768
Eldawy, A., and Mokbel, M. (2015). “Spatialhadoop: a mapreduce framework for spatial data,” in ICDE (Seoul).
Gaede, V., and Günther, O. (1998). Multidimensional access methods. ACM Comput. Surv. 30, 170–231. doi: 10.1145/280277.280279
Gonzalez, J. E., Xin, R. S., Dave, A., Crankshaw, D., Franklin, M. J., and Stoica, I. (2014). “Graphx: Graph processing in a distributed dataflow framework,” in OSDI (Broomfield, CO).
Hagedorn, S., Götze, P., and Sattler, K.-U. (2017). “The stark framework for spatio-temporal data analytics on spark,” in BTW, eds B. Mitschang et al. (Bonn: Gesellschaft für Informatik), 20.
Kwon, Y., Balazinska, M., Howe, B., and Rolia, J. (2010). “Skew-resistant parallel processing of feature-extracting scientific user-defined functions,” in SoCC (Indianapolis, IN).
Kwon, Y., Balazinska, M., Howe, B., and Rolia, J. (2012). “Skewtune: Mitigating skew in mapreduce applications,” in SIGMOD (Scottsdale, AZ)
Lu, W., Shen, Y., Chen, S., and Ooi, B. C. (2012). “Efficient processing of K nearest neighbor joins using mapreduce,” in Proc. VLDB Endow. (Istanbul).
Memarzia, P., Patrou, M., Alam, M. M., Ray, S., Bhavsar, V. C., and Kent, K. B. (2019). “Toward efficient processing of spatio-temporal workloads in a distributed in-memory system,” in 2019 20th IEEE International Conference on Mobile Data Management (MDM) (Hong Kong), 118–127.
Mingjie, T., Yongyang, Y., Walid, G. A., Qutaibah, M. M., Mourad, O., and Ahmed, R. (2016). Locationspark: A Distributed In-Memory Data Management System for Big Spatial Data. Purdue technical report. Purdue University in West Lafayette.
Nishimura, S., Das, S., Agrawal, D., and Abbadi, A. (2011). “MD-Hbase: A scalable multi-dimensional data infrastructure for location aware services,” in MDM 11.
Pandey, V., Kipf, A., Neumann, T., and Kemper, A. (2018). How good are modern spatial analytics systems? VLDB18 11, 1661–1673. doi: 10.14778/3236187.3236213
Samet, H. (2005). Foundations of Multidimensional and Metric Data Structures. Morgan Kaufmann Publishers Inc.
Shvachko, K., Kuang, H., Radia, S., and Chansler, R. (2010). “The hadoop distributed file system,” in MSST (Incline Village, NV).
Sowell, B., Salles, M. V., Cao, T., Demers, A., and Gehrke, J. (2013). “An experimental analysis of iterated spatial joins in main memory,” in Proc. VLDB Endow. (Trento).
Tang, M., Yu, Y., Aref, W. G., Mahmood, A. R., Malluhi, Q. M., and Ouzzani, M. (2019). Locationspark: in-memory distributed spatial query processing and optimization. CoRR abs/1907.03736.
Tang, M., Yu, Y., Aref, W. G., Malluhi, Q., and Ouzzani, M. (2016). “Locationspark: a distributed in-memory data management system for big spatial data,” in VLDB (New Delhi).
Xia, C., Lu, H., Chin, B., and Hu, O. J. (2004). “Gorder: An efficient method for knn join processing,” in VLDB (Toronto, ON).
Xie, D., Li, F., Yao, B., Li, G., Zhou, L., and Guo, M. (2016). “Simba: efficient in-memory spatial analytics,” in SIGMOD (San Francisco, CA).
Yu, J., Wu, J., and Sarwat, M. (2015). “Geospark: a cluster computing framework for processing large-scale spatial data,” in SIGSPATIAL (Seattle, WA).
Keywords: spatial data, query processing, in-memory computation, parallel computing, query optimization
Citation: Tang M, Yu Y, Mahmood AR, Malluhi QM, Ouzzani M and Aref WG (2020) LocationSpark: In-memory Distributed Spatial Query Processing and Optimization. Front. Big Data 3:30. doi: 10.3389/fdata.2020.00030
Received: 12 February 2020; Accepted: 05 August 2020;
Published: 16 October 2020.
Edited by:
Andreas Zuefle, George Mason University, United StatesReviewed by:
Suprio Ray, University of New Brunswick Fredericton, CanadaCopyright © 2020 Tang, Yu, Mahmood, Malluhi, Ouzzani and Aref. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yongyang Yu, eW9uZ3lhbmd5dUBmYi5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.