Pore-Level Study of Syngas Production From Fuel-Rich Partial Oxidation in a Simplified Two-Layer Burner

We performed pore-level simulation of fuel-rich partial oxidation of a CO₂/CH₄ mixture in a two-dimensional porous burner with staggered arrangement of discrete particles. The chemistry was treated with detailed chemical kinetics GRI-Mech 1.2, and surface-to-surface radiation was taken into account by the discrete ordinates (DO) model. The predicted results were validated against the available experimental data and results by the volume-averaged method. The predicted main syngas products (CO, H₂, and CO₂) agreed well with the experimental data for the whole investigation range; it indicated that the pore-level simulation could precisely predict syngas productions from fuel-rich partial oxidation in a two-layer burner with the simplified arrangement of porous media. Variations of species, temperature, and velocity within the pores were presented and discussed. The predicted molar fractions of CO, H₂, CO₂, H₂O, etc. over the pores between particles were highly two-dimensional; the flame thickness was on the order of the particle diameter (2.5 mm) and smaller than the particle diameter. The predicted area-weighted average temperatures were greater than the experiments due to the ignorance of the heat loss to the surroundings through burner walls. The effect of CO₂ adding on syngas production is examined.

Highlights

- Prediction of syngas production in pore level with detailed chemical mechanism.

- Surface-to-surface radiation is considered.

- The predicted velocities, temperatures, and species are highly two-dimensional.

- The maximum local velocity in the pores is 17.4 times of the interstitial gas velocity.

- 2D pore level with simplified geometry captures the syngas components.

Introduction

Porous media burners have been widely used for syngas production from fuel-rich partial oxidation in porous media (Kennedy et al., 1999). A review by Oliveira and Kaviany (2001) examined the non-equilibrium of transport processes for combustion in porous media. Mujeebu (2016) presented a detailed review of hydrogen and syngas production by superadiabatic combustion. He pointed out that modeling was still an open problem and the effect of porous structures on syngas production needs further investigation.

The concept of employing superadiabatic combustion for hydrogen production was first reported by Weinberg et al. (1988), who experimentally proved that fuel-rich combustion can be maintained in spouted beds. Two types of porous burner for syngas production can be found in the literature based on porous material or its structure. For the first type, burners filled with homogeneous media were used, in which the combustion wave propagated in the upstream or downstream direction of the flow, mainly depending on the equivalence ratio and mixture velocity (Drayton et al., 1998; Kennedy et al., 2000).

To confine the combustion wave within packed bed, Kennedy et al. (1999) proposed and developed reciprocal flow burner (RFB) for syngas production. Rich flammability limit was successfully extended to an equivalence ratio of 8 for methane/air mixture. Zheng et al. (2012) modeled RFB with external heat source using a one-dimensional two-temperature model with GRI-Mech 1.2. Gonzalez et al. (2018) conducted an experimental study on syngas production from biogas and polyethylene in a porous burner; it was shown that the conversion efficiency was increased by the presence of polyethylene. Futko (2003) analyzed the chemical structure of fuel-rich partial oxidation in a porous burner with the use of skeleton diagrams and sensitivity analysis, and they suggested that combustion waves could be divided into three regions based on heat release: a preheating zone, an exothermic zone characterized by partial oxidation of methane, and an endothermic zone with the conversion processes.

For the second approach, burners with different porous material or structures and two-layer porous burners were used to confine the flame near the interface of two sections under a certain range of equivalence ratio and gas velocity (Pedersen-Mjaanes et al., 2005). Zeng et al. (2017) presented an experimental and numerical study on the influence of adding CO₂ on syngas production in a two-layer burner. In their experimental study, the conversion efficiency was found to be increased from 39.1 to 45.3% when the molar ratio of CO₂ to CH₄ was increased from 0 to 1. They conducted a numerical study applying a two-dimensional two-temperature model based on the volume-averaged treatment. In their experimental study (Wang et al., 2018), the burner was optimized based on conversion efficiency, which was determined to be composed of 2.5-mm pellets in the upstream section and 7.5-mm pellets in the downstream section.

Volume-averaged treatment (Liu et al., 2009; Li et al., 2015; Yang et al., 2018; Fan et al., 2019) and pore-level simulation on porous media combustion have been applied for last three decades with special attention on fuel-lean combustion. Much of early work was limited to simple geometry with symmetry or periodic boundary conditions due to computational limitations. Sahraoui and Kaviany (1994) presented simulations of premixed combustion in packed bed for fuel-lean methane/air mixture with one-step chemistry. The volume-averaged method and the pore-level model were applied to study the superadiabatic effect, flame structure, and flame speed. Their pore-level model revealed that the significant variation of temperature and species concentration occurred over pores. However, solid radiation was ignored in their computations to save computational cost. Hackert et al. (1999) extended the work of Sahraoui and Kaviany (1994) by consideration of solid phase radiation.

Pereira et al. (2010) numerically studied porous media diffuser reformer using quasi-1D and three-dimensional models. Fuel-rich partial oxidation in the porous media was simulated by quasi-1D model with 12-step reduced chemistry. Bedoya et al. (2015) presented a comprehensive study of premixed combustion in porous media with special attention on the effects of pressure and equivalence ratio on flame speed. Both the volume-averaged model and the pore-level method were employed for three different porous burners. The three-dimensional porous structure for simulations was reconstructed with the help of computed tomography from a real sample of porous media. Considerable variation of temperature along space coordinate was predicted by the pore-level model.

Shi et al. (2017) reported combustion characteristics of fuel-lean mixture in packed bed made of discrete particles. They found significant thermal non-equilibrium between the same phase and interphase. Recently, Jiang et al. (2017, 2018) modeled filtration combustion in a random packed bed filled with pellets by large eddy model, and the turbulent-flame interaction in porous media with special porous structure was quantitatively analyzed.

As reviewed above, numerical studies on syngas production based on volume-averaged treatment have been extensively studied with different chemical kinetics for several fuels and rather development has been made. However, volume-averaged treatments filter out the detailed information at the smaller scales (Oliveira and Kaviany, 2001). Meanwhile, measurements of velocities, species profiles, temperature distributions, and flame structures were often difficult due to the obstacle of porous media. The knowledge on detailed information in pore level was scarce. To the authors' best knowledge, no pore-level numerical study on the syngas production was reported.

The detailed local simulations helped to understand the physics of filtration combustion in pore level. Faced with the complex three-dimensional geometry structures and high computational cost, pore-level simulation for simplified geometry structures with detailed kinetics was feasible at present and might present some principles for the future three-dimensional pore-level simulation with complex structures of porous media.

The aim of this work was to investigate syngas production from partial oxidation of fuel-rich CO₂/CH₄ mixture in a two-layer burner made of two-dimensional simplified geometries. The chemistry was treated with detailed chemical kinetics Gri-Mech 1.2 and surface-to-surface radiation between the pellets was taken into account using the discrete ordinates (DO) model.

Physical Model

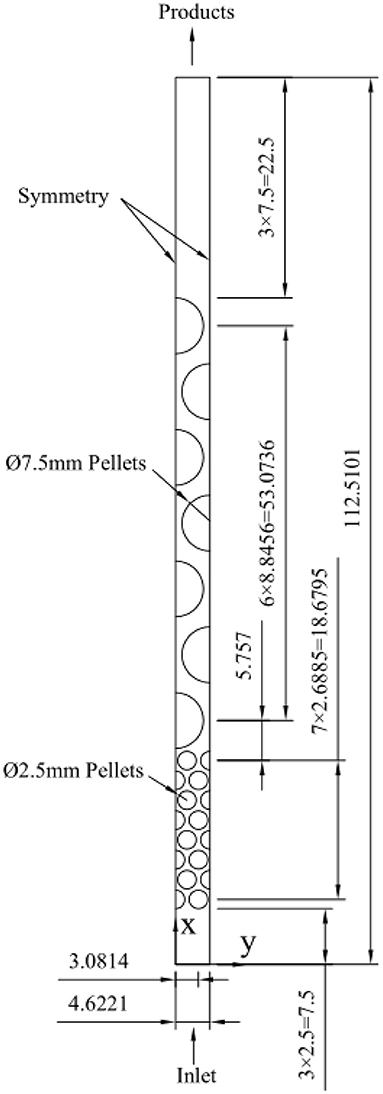
A two-layer burner developed and tested by Zeng et al. (2017) is considered in computations. The porous burner was composed of 2- to 3-mm alumina pellets with a length of 20 mm in the upstream and 7.5-mm alumina pellets in the downstream that was 60 mm long. The burner developed by Zeng et al. (2017) is a random packed bed, and three-dimensional pore-level simulations of syngas production in this random packed bed with detailed kinetics are infeasible due to computational limitations. Meanwhile, it is very difficult to use a 2D direct model for the random packed bed. Even for the 3D simple cubic and body center cubic packing, it is difficult to choose a 2D representative part to represent 3D geometry. In this study, the random packed bed is simplified to a two-dimensional structural arrangement of discrete cylinder particles. The process of reconstructing geometries is as follows. For a packed bed with 2.5-mm pellets in the upstream section and 7.5-mm pellets in the downstream section, we assume that all the particles are arranged in equilateral triangles and the corresponding porosities are computed as ε = 0.375+0.34d/D, where d and D are the diameter of the particle and burner, respectively. Under the above assumptions, the number of pellets and the distance between the neighboring pellets in the computational domain are determined. For simplification, just two rows of 2.5-mm particles and one row of 7.5-mm particles with symmetric boundary conditions at the right and left of the selected rows have been considered in the present study, as shown in Figure 1. The packed bed contains 16 cylindrical particles with a diameter of 2.5 mm in the upstream section and seven cylindrical particles with a diameter of 7.5 mm in the downstream section. The lengths of the corresponding zone filled with 2.5- and 7.5-mm particles are 21.1795 and 60.5736 mm, which are close to the lengths of the modeled burner (Zeng et al., 2017). It extends 7.5 mm in the upstream (inlet section) and 22.5 mm in the downstream (outlet section).

FIGURE 1

Figure 1. Schematic of the two-layer burner.

To simplify the problem, the following assumptions are made:

(1) The pellets are opaque and inert homogeneous; solid surface scattering is ignored.

(2) The surface-to-surface radiation and gas radiation are taken into account and computed by the DO model. The gas is gray gas and does not scatter; the refractive index of the gas is one.

(3) The flow of gas mixture in the packed bed is assumed to be laminar.

(4) Heat loss through burner walls to the surrounding is assumed to be proportional to the heat loss coefficient β and the difference between the local and ambient temperature.

Under the above assumptions, a set of differential equations can be obtained.

Continuity equation

$\begin{array}{ll}\nabla ·({\rho }_g\text{v})=0& (1)\end{array}$

where ρ_g represents the gas density and vdenotes the velocity vector.

Momentum equation

$\begin{array}{ll}\nabla ·({\rho }_g\text{v}{v}_i)=\nabla ·(\mu \nabla v_i)-\frac{\partial P}{\partial x_i}& (2)\end{array}$

where v_i represents the horizontal or vertical velocity, μ is dynamic viscosity, and P is the pressure.

Gas phase energy equation

$\begin{array}{l}\hfill \nabla ·({\rho }_g{c}_g\text{v}{T}_g)=\nabla ·({\lambda }_g\nabla T_g)+{\displaystyle \sum _i}{\omega }_i{h}_i{W}_i-\nabla ·q_r\\ -\beta (T_g-T_0)& (3)\end{array}$

where T_g, λ_g, c_g are the gas temperature, thermal conductivity, and specific heat, respectively. ω_i, W_i are the chemical reaction rate and molecular weight of species i, respectively. β is heat loss coefficient (Contarin et al., 2003). q_R is radiation flux, obtained by the DO model coupled to the model for the properties of gas mixture. The DO model solves radiative transfer equation (RTE) in the direction $\overrightarrow{s}$ as a field equation. For model gas radiation, we assume that the gas is gray gas and does not scatter, the refractive index of the gas is one, and the RTE for the gas phase in this study is simplified to:

$\begin{array}{l}\nabla ·(I(\overrightarrow{r},\overrightarrow{s})\overrightarrow{s})+\alpha I(\overrightarrow{r},\overrightarrow{s})=\alpha \sigma T^4\surd \pi \end{array}$

where $I(\overrightarrow{r},\overrightarrow{s})$ is radiation intensity, σ is Stefan–Boltzmann constant, and α is gas absorption coefficient and computed by weighted sum of gray gases model. The heat source term due to radiation that appears in Equation (3) is calculated from RTE: $\nabla ·q_r=4\alpha \sigma T^4-\alpha G$, where G is incident radiation.

Solid phase energy equation

$\begin{array}{ll}\nabla ·({\lambda }_s\nabla T_s)-\beta (T_s-T_0)=0& (4)\end{array}$

where T_s, λ_s is the solid temperature and thermal conductivity, respectively.

Species conservation equation

$\begin{array}{ll}\nabla ·({\rho }_g\text{v}{Y}_i)-\nabla ·({\rho }_g{D}_i\nabla Y_i)-{\omega }_i{W}_i=0& (5)\end{array}$

where D_i, Y_i is diffusion coefficient and mass fraction of species i, respectively.

Boundary Conditions

The following boundary conditions are specified in the model:

1) Inlet

$\begin{array}{l}{T}_g=T_s=300K,u=u_0,v=0\\ Y_{CH4}={Y_{CH4}}_{,in},Y_{O2}={Y_{O2}}_{,in},Y_{CO2}={Y_{CO2}}_{,in}& (6)\end{array}$

2) Outlet

$\begin{array}{ll}\frac{\partial T_g}{\partial x}=\frac{\partial T_s}{\partial x}=\frac{\partial (Y_i)}{\partial x}=\frac{\partial (u)}{\partial x}=0& (7)\end{array}$

3) Radiative heat loss from burner inlet and outlet is considered;

$\begin{array}{ll}{\lambda }_s\frac{\partial T_s}{\partial x}=-{\epsilon }_r\sigma ({T^4}_{s,\text{in}/\text{out}}-{T_0}^4)& (8)\end{array}$

ε_r is the solid surface emissivity and σ is the Stefan–Boltzmann constant.

4) At y = 0, 3.0814 mm, symmetry conditions are imposed;

$\begin{array}{ll}\frac{\partial T_g}{\partial y}=\frac{\partial T_s}{\partial y}=\frac{\partial Y_i}{\partial y}=\frac{\partial u}{\partial y}=v=0& (9)\end{array}$

At the gas–solid interfaces, the non-slip condition is imposed for gas velocity. The symbol used in this work is summarized in Table 1. Table 2 presents the values of velocity, temperature, and pressure at the burner inlet.

TABLE 1

Table 1. Symbols used in this work.

TABLE 2

Table 2. Numerical values at boundary inlet.

Initial Conditions, Material Porperties, and Solution

The governing Equations (1)–(5) with the boundary conditions are numerically solved by a CFD software Fluent 15.0. The chemistry is treated with detailed kinetics Gri-Mech 1.2; it includes 32 species and 177 reactions. The thermal and transport properties of gas are obtained from the Chemkin and Tranfit packages (Kee et al., 1986). These properties and detailed reaction mechanism are imported into Fluent 15.0. Detailed chemical mechanisms are invariably numerically stiff and compute-intensive. However, we used direct integration for the chemical reaction. Fluent 15.0 computes the Arrhenius rate for the laminar flow. The thermal conductivity of the alumina pellets is specified as polynomial functions of the temperature (Munro, 2010). The density of pellets is specified as 3,984 kg/m³. The absorption coefficient and emissivity of the pellets are set to be 80 m⁻¹ and 0.4 (Henneke and Ellzey, 1999).

The pressure field is solved using the SIMPLE method. At the interface of the upstream and downstream sections, the solid temperature of pellets is set to be 2,200 K to model the ignition process. We have tested the sensitivity of this initial heating to the predicted results. It is shown that the ignition fails when the initial heating temperature is smaller than 2,200 K. A residual error of 10⁻⁶ for energy equations and 10⁻³ for all other equations are taken as convergence criteria.

The conversion efficiency is defined as (Zeng et al., 2017):

$\begin{array}{ll}{\eta }_{e-s}=\frac{Y_{CO}\times LH{V}_{CO}+Y_{H2}\times LH{V}_{H2}}{Y_{CH4,in}\times LH{V}_{CH4}}& (10)\end{array}$

where LHV_CH4, LHV_CO, and LHV_H2, are the low heating value of CH₄, CO, and H₂, respectively.

Mesh Independence Study

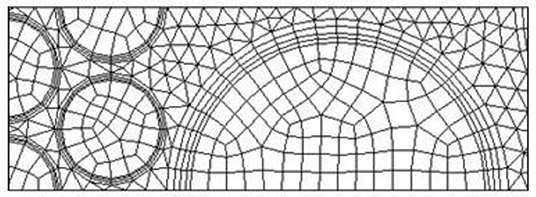
As shown in Figure 1, the computational domain includes inlet section, outlet section, and solid and fluid zone. The fluid zone is constantly changing and the fluid path is tortuous. Chemical reaction takes place at the fluid zone, intense convective heat transfer occurs near the particle surfaces in the fluid side, and thus more mesh is expected in the fluid zone. In this study, non-uniform grid system is used in the computation, with finer grid in the fluid zone. Three mesh configurations are analyzed during the convergence study for three levels, coarse (mesh 1), average (mesh 2), and fine (mesh 3). Table 3 shows the details of the mesh size and mesh type in the computations. Figure 2 shows the mesh in the vicinity of the interface between the 2.5- and 7.5-mm pellets. Three prism layers are applied at the fluid side for all the particle surfaces. Quad mesh is used in the solid zone, and triangle mesh is used in the fluid zone.

TABLE 3

Table 3. Mesh configurations.

FIGURE 2

Figure 2. Mesh in the vicinity of the interface between the two sections.

To estimate the influence of the mesh resolution, we analyze the average temperature and normalized velocity (divided by u₀/ε) in the burner. The average temperature is defined as average value perpendicular to the flow direction. The heating of the cold particle (300 K) with hot air (1,600 K) is calculated, including the radiation, but the chemical reaction is not considered; other parameters and the solution procedure are the same to the full problem.

Figure 3 presents the predicted average temperature and normalized velocity for the three mesh configurations. It can be seen that the average temperature and normalized velocity for mesh 1 differs considerably from other configurations. It is shown that mesh resolution has a larger impact on flow parameter than the heat transfer. The predicted average temperatures by mesh 2 and mesh 3 are almost the same over the entire range. The predicted normalized velocity demonstrates the largest difference of 3.5% between mesh configurations 2 and 3. Finally, mesh 2 was used for the computation.

FIGURE 3

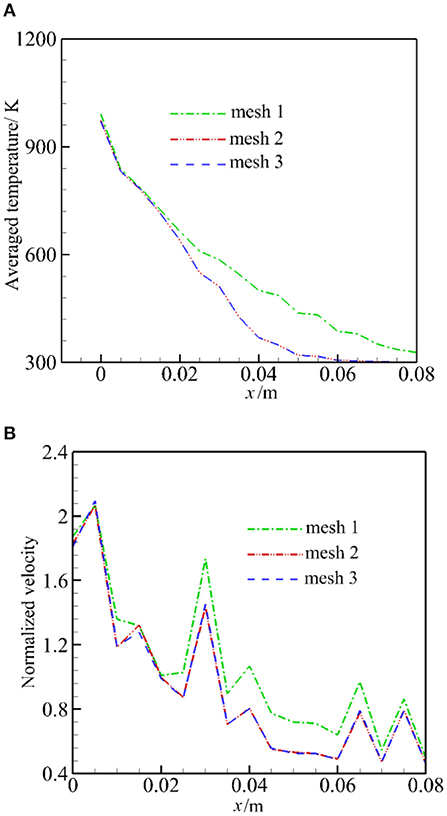
Figure 3. Averaged temperature and normalized velocity for three mesh configurations. (A) Averaged temperature. (B) Normalized velocity.

Results and Discussion

Species Profiles, Temperature Distributions, and Velocities Within Pores

In the experiment (Zeng et al., 2017), the equivalence ratio (φ) and air flow rate are set to be 1.5 and 5 L/min, while the ratio (α) between CO₂ and CH₄ is changed from 0 to 1. In the computation, for all computed cases, the equivalence ratio for methane/air mixture is set to be a fixed value of 1.5 and the mixture velocity at the burner inlet is varied due to the adding CO₂ in fuel.

Figure 4 illustrates the predicted molar fractions of CH₄, O₂, CO, H₂, H₂O, and CO₂ (X_CH4, X_O2, X_CO, X_H2, X_CO2, X_H2O), temperature, and normalized velocity near the exothermic zone for α = 0 and φ = 1.5. One can see that the distributions of syngas components in the pores are highly two-dimensional. Slight decreases in X_CH4 and X_O2 are observed between the second and third rows of the particles. This indicates that CH₄ begins to break down and a very smaller O₂ is consumed in the preheating zone. Then, significant decreases in X_CH4 and X_O2 are observed within the pores between the second row of particles and it means that extensive chemical reaction occurs within a small region. The thickness of the exothermic zone is on the order of pellet diameter (2.5 mm) and smaller than the pellet diameter. Predictions (Zeng et al., 2017) by the volume-averaged method showed that the thickness of flame zone was smaller than 3 mm for this case. Our predictions of flame thickness agree with the results by the volume-averaged method. The main syngas components, CO and H₂, are being formed over the pores between the second and third rows of particles, and then a slight reduction in X_CO and increase in X_H2 are revealed in the post-flame zone. X_H2O peaks just after the exothermic zone and a slight decrease in X_H2O is observed in the post-flame zone, whereas X_CO2 still slightly increases after the exothermic zone. The small variations of molar fraction of CO, CO₂, H₂, and H₂O in the endothermic zone are captured by our model. For fuel-rich partial oxidation in porous media, the water–gas shift reaction CO+H2O → H2+CO2 is an important reaction in the reforming process, which leads to a slight increase in X_H2 and X_CO2 and a slight decrease in X_CO and X_H2O.

FIGURE 4

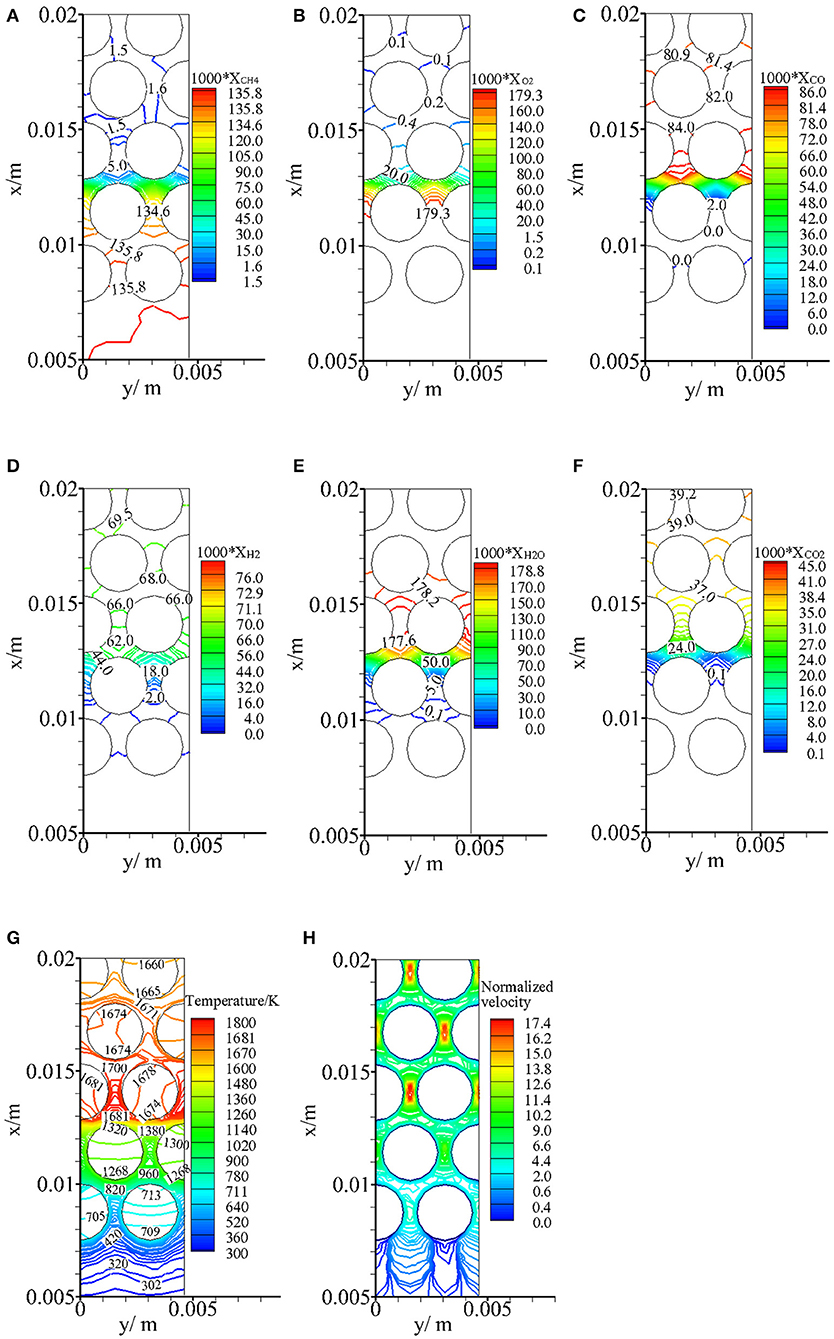
Figure 4. Predicted molar fractions of CH₄, O₂, CO, H₂, H₂O, CO₂, temperature profiles, and normalized velocity distributions near the exothermic zone for α = 0 and ϕ = 1.5. (A) X_CH4, (B) X_O2, (C) X_CO, (D) X_H2, (E) X_H2O, (F) X_CO2, (G) Temperature (K), and (H) Normalized velocity.

The high gas temperature zone is located just downstream the reaction zone. In the post-flame zone, as shown in Figure 4G, the temperature difference within the same particle is rather small and can be negligible. This is because adequate heat exchange takes place between the gas and solid phases through convective heat transfer, and the solid thermal conductivity is greater compared to that of the gas phase. However, in the preheating region, obvious thermal non-equilibrium is observed within the same pellet. This is the result of reaction heat redistribution and multimode heat transfer mechanisms in the packed bed. The combustion takes place near the second row of the particles, and part of the reaction heat is stored in the porous media around the reaction zone through convective heat transfer between the gas and solid phases. Then, solid radiation occurs between the heated particles and the neighboring particles. The particles of the first row are heated via surface-to-surface radiation. Thus, heat recirculation is realized through solid radiation from the downstream high-temperature region to the upstream low-temperature region. As a result, the incoming fresh mixtures prior to entering the combustion zone are preheated by gas radiation and through convective heat transfer between the gas and solid phases. It is shown in Figure 4G that the gas mixture is substantially preheated before entering the reaction zone.

The normalized velocity is defined as the ratio of the predicted local velocity to the average interstitial gas velocity. As shown in Figure 4H, the maximum normalized velocity reaches up to 17.4 and this means that the maximum velocity in the pores is 17.4 times of the interstitial gas velocity. The distribution of normalized velocity is periodic by the distance of particle diameter and this is due to the staggered arrangement of the particles.

Temperature Distributions

Figure 5 presents the experimental values, the predicted solid temperatures by Zeng et al. (2017), and the predicted averaged temperatures along the flow direction for φ = 1.5 and α = 0, 1. It is noted that the experimental values and predictions (Zeng et al., 2017) in Figure 5 are the temperatures along the burner centerline. To compare the predicted temperatures by the pore-level model with the experiments and predictions, the predicted temperatures in this work in Figure 5 are area-weighted average temperatures in the line perpendicular to the flow direction. Our prediction shows the same trend as experiments, but the predicted averaged temperatures are greater than the experiments and the predictions (Zeng et al., 2017) especially for α = 0. The difference is mainly due to the model used in present study. In our model, radiation heat loss to the surrounding from the burner inlet and outlet is considered. However, only part of the burner in the flow direction is considered and symmetry conditions are used, heat loss to the surroundings through burner walls is taken into account by an empirical formula. Zeng et al. (2017) modeled the syngas production using the same physics model, in their two-dimensional model, heat loss to the surroundings through the burner walls was taken into account and good agreement between their predictions and experiments was observed compared to our model. For α = 1, both the predictions by Zeng et al. (2017) and this work show that the flame shifts slightly to downstream compared to the experimental results, and the predicted T_s and the average temperature agree well with the experiment when the measurement error is taken into account.

FIGURE 5

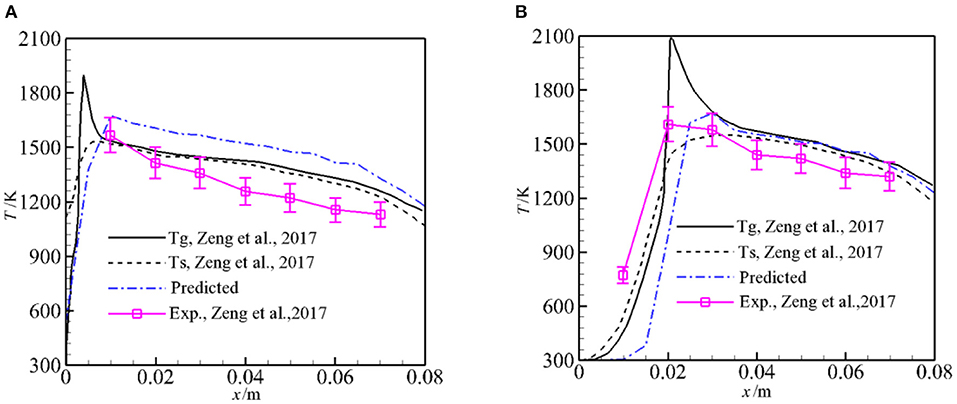
Figure 5. Predicted temperatures for ϕ = 1.5 and α = 0, 1. (A) Predicted temperatures for α = 0 and ϕ = 1.5. (B) Predicted temperatures for α = 1 and ϕ = 1.5.

Combustion Products and Conversion Efficiencies

Figure 6 shows the predicted molar fraction of major combustion products (H₂, CO, CO₂, CH₄) in the exhaust gases as a function of α for φ = 1.5, and experimental results and numerical predictions by Zeng et al. (2017) are also presented for comparison. It is shown in Figure 6 that X_CO and X_CO2 increases, while X_H2 and X_CH4 reduces when α is increased from 0 to 1. It can be noted that our model can successfully capture the syngas components with different α. The predictions by our model and Zeng et al. (2017) show good agreement with the experimental results for the whole range of α. Our predictions of X_H2 are slightly greater than the experimental values, and the differences between the predictions and experiments are reasonable when the measurement error is taken into account. The amount of unburned CH₄ in the exhaust gases is very small and X_CH4 is overpredicted by our model. It is noted that our model has almost the same accuracy in predicting the major combustion products as the volume-averaged method used by Zeng et al. (2017). This indicates that modeling syngas production in pore level with staggered arrangement of discrete particles is feasible and the predictions are reliable. Meanwhile, as shown in Figure 4, detailed information in the pores such as velocity profiles, temperature distributions, and syngas components can be obtained by the present model; this information is often difficult to measure in experiments, and it is very important to deeply understand the physics of syngas combustion in porous media.

FIGURE 6

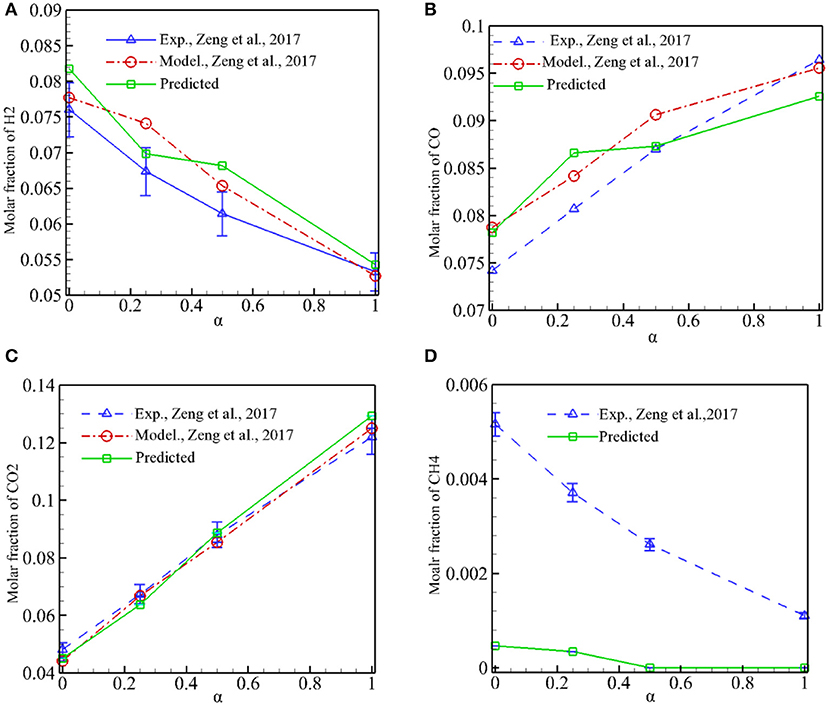
Figure 6. Predicted molar fraction of H₂, CO, CO₂, and CH₄ in the exhaust gases as a function of α for ϕ = 1.5. (A) Predicted X_H2 in the exhaust gases. (B) Predicted X_CO in the exhaust gases. (C) Predicted X_CO2 in the exhaust gases. (D) Predicted X_CH4 in the exhaust gases.

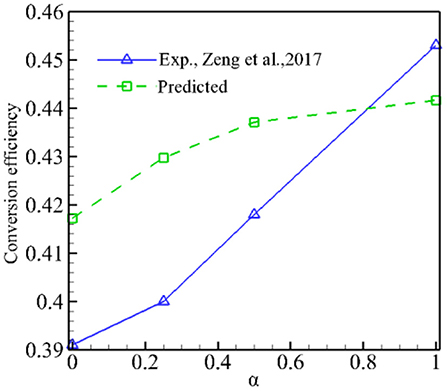
Figure 7 presents the predicted conversion efficiency of syngas production as well as experimental values as a function of α for φ = 1.5. Both the predictions and experiments show that the conversion efficiency increases with α; it indicates that adding CO₂ in the fuel can increase the conversion efficiency. Our model predicts the same trend as experiments, but the conversion efficiency is overpredicted for 0 ≤ α ≤ 0.5 compared to the experimental results. Again, this is due to the fact that the model overpredicts the combustion temperature and therefore the conversion efficiency.

FIGURE 7

Figure 7. Predicted conversion efficiency as a function of α for ϕ = 1.5.

Conlusions

A numerical study on syngas production from fuel-rich partial oxidation in a two-layer burner made of staggered arrangements of particles is conducted using detailed chemistry mechanism GRI-Mech 1.2. The predicted results for the temperature, syngas production of components, and conversion efficiency are compared with experiments and the results from volume-averaged method. The major conclusions are as follows:

(1) The pore-level modeling of syngas production with the simplified discrete particles captures the feature of fuel-rich combustion in pore level. The model can successfully capture the syngas components with different molar ration of CO₂/CH₄.

(2) The thermal non-equilibrium in the same particle is observed in the burner. The thermal non-equilibrium varies along the flow direction and is not obvious in the post-flame zone.

(3) The detailed information of syngas components, temperature, and velocity over the pores is presented with the pore-level model, which is difficult to get in experiment.

(4) The predicted molar fractions of CH₄, CO, H₂, and CO₂ in the pores are highly two-dimensional. The maximum gas velocity in the pores is 17.4 times that of the interstitial gas velocity.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

JS, MM, and HL conceived and designed the study. HL and YL analyzed the data. MM and YS wrote the manuscript.

Funding

The authors wish to acknowledge the support to this work by the National Natural Science Foundation of China (No. 51876107) and the General Projects of Key R&D Plans in Shaanxi Province (2018SF-387).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Bedoya, C., Dinkov, I., Habisreuther, P., Zarzalis, N., Bockhorn, H., and Parthasarathy, P. (2015). Experimental study, 1D volume-averaged calculations and 3D direct pore level simulations of flame stabilization in porous inert media at elevated pressure. Combust. Flame 16, 3740–3754. doi: 10.1016/j.combustflame.2015.07.012

CrossRef Full Text | Google Scholar

Contarin, F., Saveliev, A. V., Fridman, A. A., and Kennedy, L. A. (2003). A reciprocal flow filtration combustor with embedded heat exchangers: numerical study. Int. J. Heat Mass Transf. 46, 949–961. doi: 10.1016/S0017-9310(02)00371-X

CrossRef Full Text | Google Scholar

Drayton, M. K., Saveliev, A. V., Kennedy, L. A., Fridman, A. A., and Li, Y. E. (1998). Syngas production using superadiabatic combustion of ultra-rich methane-air mixtures. Symp. Combust. 27, 1361–1367. doi: 10.1016/s0082-0784(98)80541-9

CrossRef Full Text | Google Scholar

Fan, A. W., Li, L. H., Yang, W., and Yuan, Z. L. (2019). Comparison of combustion efficiency between micro combustors with single- and double-layered walls: a numerical study. Chem. Eng. Process 137, 39–47. doi: 10.1016/j.cep.2019.02.004

CrossRef Full Text | Google Scholar

Futko, S. I. (2003). Kinetic analysis of the chemical structure of waves of filtration combustion of gases in fuel-rich compositions. Combust. Explo Shock Waves 39, 437–447. doi: 10.1023/A:1024786805591

CrossRef Full Text | Google Scholar

Gonzalez, H., Caro, S., Toledo, M., and Olguin, H. (2018). Syngas production from polyethylene and biogas in porous media combustion. Int. J. Hydr. Energy 43, 4294–4304. doi: 10.1016/j.ijhydene.2018.01.050

CrossRef Full Text | Google Scholar

Hackert, C. L., Ellzey, J. L., and Ezekoye, O. A. (1999). Combustion and heat transfer in model two-dimensional porous media. Combust. Flame 116, 177–191. doi: 10.1039/A903185E

CrossRef Full Text | Google Scholar

Henneke, M. R., and Ellzey, J. L. (1999). Modeling of filtration combustion in a packed bed. Combust. Flame 117, 832–840. doi: 10.1016/S0010-2180(98)00129-1

CrossRef Full Text | Google Scholar

Jiang, L. S., Liu, H. S., Suo, S. Y., and Xie, M. Z. (2018). Pore-scale simulation of flow and turbulence characteristics in three-dimensional randomly packed beds. Powder Technol. 338, 197–210. doi: 10.1016/j.powtec.2018.06.013

CrossRef Full Text | Google Scholar

Jiang, L. S., Liu, H. S., and Xie, M. Z. (2017). Pore-scale simulation of vortexcharacteristics in randomly packed beds using LES/RANS models. Chem. Eng. Sci. 177, 431–444. doi: 10.1016/j.ces.2017.11.040

CrossRef Full Text | Google Scholar

Kee, R. J., Dixon, G. L., Warnatz, J., Coltrin, M. E., and Miller, J. A. (1986). A Fortran Computer Code Package for the Evaluation of Gas Phase Multi-component Transport Properties. Report SAND86-8246. Sandia National Laboratories.

Google Scholar

Kennedy, L. A., Bingue, J. P., Saveliev, A. V., and Foutko, S. I. (2000). Chemical structures of methane-air filtration combustion waves for fuel-lean and fuel-rich conditions. Proc. Combust. Instit. 28, 1431–1438. doi: 10.1016/S0082-0784(00)80359-8

CrossRef Full Text | Google Scholar

Kennedy, L. A., Saveliev, A. V., and Fridman, A. A. (1999). Proceedings of the Mediterranean Combust, Symposium (Naples), 105–139.

Google Scholar

Li, J., Wang, Y. T., Shi, J. R., and Liu, X. L. (2015). Dynamic behaviors of premixed hydrogen–air flames in a planar micro-combustor filled with porous medium. Fuel 145, 70–78. doi: 10.1016/j.fuel.2014.12.070

CrossRef Full Text | Google Scholar

Liu, H., Dong, S., Li, B. W., and Chen, H. G. (2009). Parametric investigations of premixed methane–air combustion in two-section porous media by numerical simulation. Fuel 89, 1736–1742. doi: 10.1016/j.fuel.2009.06.001

CrossRef Full Text | Google Scholar

Mujeebu, A. M. (2016). Hydrogen and syngas production by superadiabatic combustion-a review. Appl. Energy 173, 210–224. doi: 10.1016/j.apenergy.2016.04.018

CrossRef Full Text | Google Scholar

Munro, M. (2010). Evaluated material properties for a sintered alpha-alumina. J. Am. Ceram. Soc. 80, 1919–1928. doi: 10.1111/j.1151-2916.1997.tb03074.x

CrossRef Full Text | Google Scholar

Oliveira, M., and Kaviany, M. (2001). Nonequilibrium in the transport of heat and mass reactants in combustion in porous media. Prog. Energy Combust. Sci. 27, 523–545. doi: 10.1016/S0360-1285(00)00030-7

CrossRef Full Text | Google Scholar

Pedersen-Mjaanes, H., Chan, L., and Mastorakos, E. (2005). Hydrogen production from rich combustion in porous media. Int. J. Hydrog. Energy 30, 579–592. doi: 10.1016/j.ijhydene.2004.05.006

CrossRef Full Text | Google Scholar

Pereira, J. M. C., Mendes, M. A. A., Trimis, D., and Pereira, J. C. F. (2010). Quasi-1D and 3D TPOX porous media diffuser reformer model. Fuel 89, 1928–1935. doi: 10.1016/j.fuel.2010.01.011

CrossRef Full Text | Google Scholar

Sahraoui, M., and Kaviany, M. (1994). Direct simulation vs volume-averaged treatment of adiabatic, premixed flame in a porous medium. Int. J. Heat Mass Transfer 37, 2817–2834. doi: 10.1016/0017-9310(94)90338-7

CrossRef Full Text | Google Scholar

Shi, J. R., Xiao, H. X., Li, J., Li, N., Xia, Y. F., and Xu, Y. N. (2017). Two-dimensional pore-level simulation of low-velocity filtration combustion in a packed bed with staggered arrangements of discrete. Combust. Sci. Technol. 189, 1260–1276. doi: 10.1080/00102202.2017.1282472

CrossRef Full Text | Google Scholar

Wang, Y. Q., Zeng, H. Y., Shi, Y. X., and Cai, N. S. (2018). Methane partial oxidation in a two-layer porous media burner with Al₂O₃ pellets of different diameters. Fuel 217, 45–50. doi: 10.1016/j.fuel.2017.12.088

CrossRef Full Text | Google Scholar

Weinberg, F. J., Bartleet, T. G., Carleton, F. B., Rimbotti, P., Brophy, J. H., and Manning, R. P. (1988). Partial oxidation of fuel-rich mixtures in a spouted bed combustor. Combust. Flame 72, 235–239.

Google Scholar

Yang, W., Li, L. H., Fan, A. W., and Yao, H. (2018). Effect of oxygen enrichment on combustion efficiency of lean H₂/N₂/O₂ flames in a micro cavity-combustor. Chem. Eng. Process 127, 50–57. doi: 10.1016/j.cep.2018.03.019

CrossRef Full Text | Google Scholar

Zeng, H. Y., Wang, Y. Q., Shi, Y. X., Ni, M., and Cai, N. S. (2017). Syngas production from CO₂/CH₄ rich combustion in a porous media burner: Experimental characterization and elementary reaction model. Fuel 199, 413–419. doi: 10.1016/j.fuel.2017.03.003

CrossRef Full Text | Google Scholar

Zheng, C., Cheng, L., Cen, K., Bingue, J. P., and Saveliev, A. (2012). Partial oxidation of methane in a reciprocal flow porous burner with an external heat source. Int. J. Hydrog. Energy 37, 4119–4126. doi: 10.1016/j.ijhydene.2011.11.142

CrossRef Full Text | Google Scholar