Extended X-Ray Absorption Fine Structure of ZrW2O8: Theory vs. Experiment

Extended x-ray absorption fine structure (EXAFS) is well-suited for investigations of structure and disorder of complex materials. Recently, experimental measurements and analysis of EXAFS have been carried out to elucidate the mechanisms responsible for the negative thermal expansion (NTE) in zirconium tungstate (ZrW₂O₈). In contrast to previous work suggesting that transverse O-displacements are largely responsible, the EXAFS analysis suggested that correlated rotations and translations of octahedra and tetrahedra within the structure are a major source. In an effort to resolve this controversy, we have carried out ab initio calculations of the structure, lattice vibrations, and EXAFS of ZrW₂O₈ based on real-space multiple-scattering calculations using the FEFF9 code and auxiliary calculations of structure and Debye-Waller factors. We find that the theoretical simulations are consistent with observed EXAFS, and show that both of the above mechanisms contribute to the dynamical structure of ZrW₂O₈.

1. Introduction

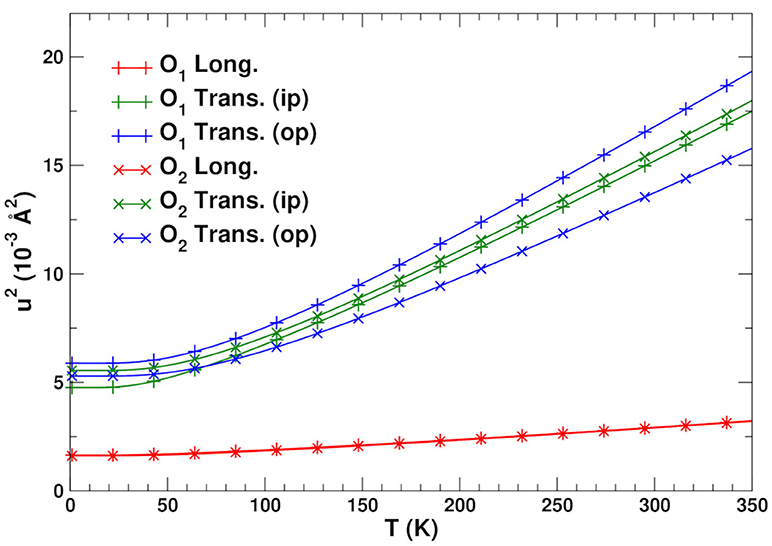
Zirconium tungstate (ZrW₂O₈) is remarkable for its large negative thermal expansion (NTE). Unlike other such materials, ZrW₂O₈ exhibits NTE over a wide range of temperatures from about 10 to 1,050 K. However, the microscopic mechanism(s) underlying its NTE is controversial. In several studies this has been associated primarily with the transverse motion of the central O atom in the Zr-O-W linkages (Figure 1).

FIGURE 1

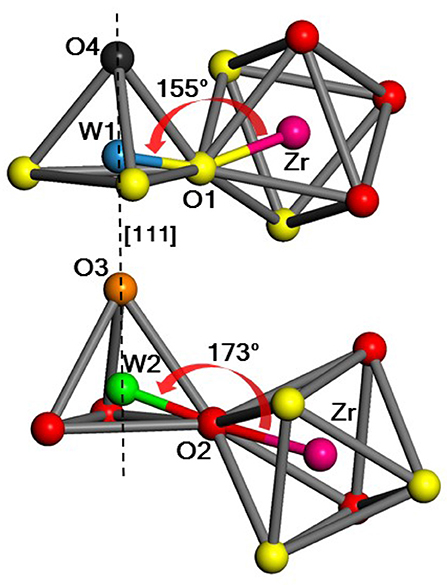
Figure 1. Portion of the unit cell showing the two possible WO₄–ZrO₆ linkages in ZrW₂O₈, with Zr (magenta), W1 (blue) and W2 (green), O1 (yellow), O2 (red), O3 (orange), O4 (black). W1, O1, and W2, O2 are the atoms that form Zr-O-W linkages with bridging angles of 155° and 173°, respectively, while the O3 and O4 atoms are only weakly linked (Table 1). [111] denotes the body diagonal direction of the unit cell.

Recently, however, an alternative mechanism based on correlated translations of the W-centered oxygen tetrahedra and rotations of Zr-centered oxygen octahedra has been proposed (Cao et al., 2002, 2003; Bridges et al., 2014). This interpretation is based on experimental investigations of ZrW₂O₈ using extended x-ray absorption fine structure (EXAFS), a technique well suited for eludicating the structure and disorder in complex materials. X-ray total scattering results are consistent with this interpretation (Bridges et al., 2014). In particular these analyses suggest that the Zr-O2-W2 linkages are quite stiff, with the implication of limited transverse O motion. In an effort to resolve the controversy, we have carried out ab initio simulations of EXAFS of ZrW₂O₈ using the real-space multiple-scattering (RSMS) code FEFF9 (Rehr et al., 2009) and associated Debye-Waller factors (Vila et al., 2007). We find that these calculations are consistent with the observed EXAFS, and show that both of the above mechanisms contribute to the dynamical structure of ZrW₂O₈.

In the remainder of this work we first summarize the lattice structure of ZrW₂O₈, the multiple-scattering theory of EXAFS, and the theory of the multiple-scattering Debye-Waller factors. Subsequently we describe the results of our simulations, followed by a summary and conclusions.

2. Theoretical Considerations

2.1. Structure of ZrW₂O₈

The first step in our approach is a detailed treatment of the ground state equilibrium structure of ZrW₂O₈. Our calculations assume a periodic equilibrium structure with a 44-atom unit cell enclosing four equivalent Zr, 8 W, and 32 O atoms. The metal atoms are centered in polyhedra with O vertices: octahedra for Zr, and tetrahedra for W. The O atoms shared between the Zr-octahedra and W-tetrahedra form Zr–O–W “linkages.” This detailed structure was refined with ab initio DFT calculations using the VASP plane-wave pseudopotential code (Kresse and Hafner, 1993, 1994; Kresse and Furthmüller, 1996a,b; Kresse and Joubert, 1999). These calculations show that the structure has a large degree of asymmetry; the octahedra are slightly irregular, and the unit cell contains Zr-O-W bond linkages with equally populated bond angles of about 155 and 173° respectively (see Figure 1 and Table 1).

TABLE 1

Table 1. Experimental and theoretical structural parameters for the 44-atom ZrW₂O₈ cell used in this work.

2.2. Multiple-Scattering EXAFS Theory

Formally, the normalized EXAFS at a given photon energy E is defined as χ = (μ−μ₀)/μ₀, where μ is the x-ray absorption coefficient and μ₀ the smooth atomic background. Theoretically χ can be represented by a sum over all possible single- (SS) and multiple-scattering (MS) paths p taken by the photoelectron following photo-absorption (Rehr et al., 2009). Assuming the thermal and structural disorder is sufficiently small, χ(k) is given by the full path expansion

$\begin{array}{ll}\chi (k)={\displaystyle \sum _p}{N}_p{\chi }_p(k)e^{-2{\sigma }_p^2{k}^2},& (1\text{a})\end{array}$

$\begin{array}{ll}{\chi }_p(k)=S_0^2\frac{\left|f_{\text{eff}}^p(k)\right|}{k{R}_p^2}sin(2k{R}_p+{\Phi }_p)e^{-2R/{\lambda }_k}.& (1\text{b})\end{array}$

Here $k=\sqrt{2(E-E_0)}$ is the wave-number of the photoelectron defined relative to threshold energy E₀, $f_{\text{eff}}^p(k)$ the effective scattering amplitude of path p, Φ_p the net scattering phase-shift, N_p the degeneracy of the path, R_p the effective- (or half-)path length, $S_0^2$ is the many-body amplitude factor, typically close to unity and path independent, λ_k is the mean free path, and ${\sigma }_p^2$ is the mean-square relative displacement (MSRD) of path p, which characterizes the path length fluctuations. Unless otherwise specified we use atomic units for the electron, e = ℏ = m = 1.

In this paper we are primarily interested in the EXAFS from the Zr K and W L₃ edges, which are relevant to previous EXAFS studies of NTE in ZrW₂O₈. In particular our study focuses on the contributions to EXAFS from the SS and MS paths linking a given Zr atom to a nearby W atom or vice versa. These paths are denoted by the scattering atoms in the path. For example, the paths Zr-W-Zr, Zr-W-O-Zr, and Zr-O-W-O-Zr also have the highest amplitude importance ratios, which are defined relative to the amplitudes for the shortest Zr-O or W-O paths. As discussed in our companion study (Vila et al., 2018), the NTE in ZrW₂O₈ can be linked to anharmonic low frequency modes with negative Grüneisen parameters. This effect is strongest for modes with transverse O-displacements, which can also involve correlated rotations and translations. Thus we also discuss the effects of such transverse motion. Details of the dominant paths including averages of effective path lengths weighted by path degeneracy are listed in Table 2, where (W1, O1) and (W2, O2) denote the W and O atoms in the Zr-O-W bond angles of 155 and 173°, respectively.

TABLE 2

Table 2. Properties of some selected Zr and W paths.

2.3. EXAFS Debye-Waller Factors

The EXAFS Debye-Waller (DW) factors $W_p=exp(-2{\sigma }_p^2{k}^2)$ provide a useful measure of damping from the correlated structural and thermal disorder in a given path. These Debye-Waller factors are essential, because they govern the exponential decay of the fine structure with increasing temperature and photoelectron energy. Our explicit calculations of ${\sigma }_p^2$ only include bond-length fluctuations (i.e., stretching contributions) in a given MS path, and neglect the usually negligible contributions from motion perpendicular to each bond (Poiarkova and Rehr, 1999a; Fornasini et al., 2004). Thus the MSRD for a given path is calculated in terms of averages over displacement-displacement correlation functions,

$\begin{array}{ll}{\sigma }_p^2=\frac{1}{4}\langle {\displaystyle \sum _{i=1}^{n_p}{\left[({\overrightarrow{u}}_i-{\overrightarrow{u}}_{i+1})·{\widehat{R}}_{i,i+1}\right]}^2}\rangle ,& (2)\end{array}$

where n_p is the number of legs in the path and 〈⋯ 〉 denotes a thermal average. However, this MSRD neglects bond-angle fluctuations, which depend on a thermal average over the effective scattering amplitude $\langle \left|f_{\text{eff}}^p(\theta )\right|\rangle$ for a given path. This effect is largest for paths with forward scattering contributions, such as the Zr-O-W linkages. Expanding to 2nd order in the bond-bending angle θ and keeping only the lowest order contributions to the average, yields a damping term that can be represented as an angular Debye-Waller factor

$\begin{array}{ll}{W}_p(\theta )=e^{-a{\sigma }_{\theta }^2},& (3)\end{array}$

$\begin{array}{l}{\sigma }_{\theta }^2=\langle {(\theta -\langle \theta \rangle )}^2\rangle ,\end{array}$

where $a=-(1/2)f_{\text{eff}}^{″}(\theta )/f_{\text{eff}}(\theta )$.

We have shown that these vibrational properties can be efficiently computed by combining DFT calculations of the dynamical matrix (DM) of lattice force constants, with a Lanczos algorithm (Vila et al., 2007). An efficient implementation based on parallelized calculations of the DMs is described in a separate paper in this collection (Vila et al., 2018), and briefly summarized below. Thermal averages such as the EXAFS mean square relative displacements ${\sigma }_p^2$ of a single or multiple scattering path p are calculated in terms of Debye integrals over the phonon projected density of states (PDOS)

$\begin{array}{ll}{\sigma }_p^2(T)=\frac{\hslash }{2{\mu }_p}{\displaystyle {\int }_0^{\infty }}\frac{1}{\omega }coth\left(\frac{\beta \hslash \omega }{2}\right){\rho }_p(\omega )d\omega ,& (4)\end{array}$

where μ_p is the reduced mass associated with the path, β = 1/k_BT, and ρ_p(ω) is the PDOS for that path (Poiarkova and Rehr, 1999a,b). Higher order cumulants such as ${\sigma }_p^{(3)}$ due to anharmonic effects are neglected, which is generally a good approximation for the relatively stiff bonds considered here. In the reminder of this work the path index subscript p is ignored unless needed for clarity.

The key system-dependent ingredient for ${\sigma }_p^2$ in Equation (4) is the PDOS ρ_p(ω). Following Poiarkova and Rehr (1999a,b) the unit-normalized PDOS is obtained from the imaginary part of path specific matrix elements of the lattice dynamical Green's function

$\begin{array}{ll}{\rho }_p(\omega )=-\frac{2\omega }{\pi }\text{Im}\langle p\left|\frac{1}{{\omega }^2-\text{D}+iϵ}\right|p\rangle .& (5)\end{array}$

Here |p〉 is a Lanczos seed vector representing an initial normalized, mass-weighted displacement along path p, and D is the dynamical matrix

$\begin{array}{ll}{D}_{jl\alpha ,j\prime l\prime \beta }={(M_j{M}_{j^{\prime }})}^{-1/2} \frac{{\partial }^{2}U[\{u_{jl\alpha }\}]}{\partial u_{jl\alpha }\partial u_{j\prime l\prime \beta }},\hfill & (6)\end{array}$

where U is the total internal energy of the system as a function of lattice coordinates, u_jlα is a displacement of atom j in unit cell l along the direction α, and M_j is the mass of atom j. The phonon Green's function is obtained from a continued fraction representation with parameters derived from the Lanczos algorithm (Haydock, 1980; Deuflhard and Hohmann, 1995). This yields a many-pole representation of the PDOS

$\begin{array}{ll}{\rho }_p(\omega )={\displaystyle \sum _{\nu =1}^{N_{\nu }}}{w}_{\nu }\delta (\omega -{\omega }_{\nu }).& (7)\end{array}$

where w_ν and ω_ν are the weights and frequencies of the N_ν poles, respectively. Typically only a few tens of poles are needed to converge calculations of ${\sigma }_p^2$.

3. Calculations

3.1. Debye-Waller Factors

The computational details of the Debye-Waller factor calculations are similar to those in Vila et al. (2018). Briefly, structural optimizations and DM calculations were performed with VASP (Kresse and Hafner, 1993, 1994; Kresse and Furthmüller, 1996a,b; Kresse and Joubert, 1999) using PAW pseudopotentials (Kresse and Joubert, 1999) with the PBEsol exchange-correlation functional (Perdew et al., 2008), and an energy cutoff of 350 eV; a k-point grid of 8 × 8 × 8 was used to achieve converged results. The lattice constant of the cell and internal reduced coordinates of the atoms in it were optimized while preserving initial lattice symmetry for computational efficiency. This DFT optimization yields a unit cell expanded by about 1% from the experimental value (see Table 1) with internal reduced coordinates that are in good agreement with experiment. Given that the internal reduced coordinates do not change with volume until the phase transition at about 430 K (Evans et al., 1999), and that the change of force constants with temperature is small in the range studied, we use the 0 K optimized structure to compute the DM. The DM is obtained using a parallelized finite difference approach with a three point centered stencil with 0.015 Å atomic displacements. The structure of the unit cell as well as the dynamical matrix are available as Supplementary Material.

Figures 2, 3 show the average calculated MSRDs for the various SS paths (W–O–W, Zr–O–Zr, W–W–W, and Zr–W–Zr), together with comparisons to experiment. Since only bond-stretching contributions are included ${\sigma }_p^2$ these results have been shifted to account for the measured structural disorder ${\sigma }_{static}^2$ which contributes additively, i.e., ${\sigma }^2={\sigma }_{\text{static}}^2+{\sigma }_{\text{stretch}}^2$. The required shift was estimated by computing the mean absolute deviation between the theoretical and experimental MSRDs over the available temperature range. The static disorder has both physical and methodological origins. The physical static disorder arises mostly from the presence of defects and distortions which are intrinsic in materials like ZrW₂O₈, while the EXAFS analysis method introduces apparent disorder by collecting paths of closely similar lengths into a single contribution with a Debye-Waller factor that reflects the length variations. Thus, for the W–O–W and Zr–O–Zr paths, which correspond to strong, well-defined bonds, the static component is very small. For the W–W–W and Zr–W–Zr paths, on the other hand, the static disorder is significant since these paths connect different WO₄ and ZrO₆ units through a variety of soft bonds. Note that the bond stretching contributions to ${\sigma }_p^2$ for these paths only involve planar fluctuations of the atoms ${\overrightarrow{u}}_i$ in the path, and that contributions to ${\sigma }_{stretch}^2$ from transverse displacements are generally negligible, even for substantial transverse O-displacements. Nevertheless, angular damping W_p(θ) may be important for paths like Zr-O-W involving forward focusing (see below). Clearly the shifted MSRDs agree well with experiment (Bridges et al., 2014). Their associated Einstein temperatures Θ_E = ℏω_E/k_B, where ω_E is the mean vibrational frequency of the PDOS for a given path, are given in Table 3. Again the agreement with experiment is satisfactory, with the largest deviations occurring for the W–W–W paths. These paths are the longest ones and thus fall in the upper range of paths lengths that can be adequately described with the present simulation cell. The slight underestimation of the MSRD for these paths would likely be reduced with a larger simulation cell which would improve the representation of the low frequency- long spatial wavelength region of the phonon density of states. The computed MSRDs are consistent with physically expected interaction strengths. For example, the W–O and Zr–O bonds are the strongest, followed by the weak, long-range interactions between the Zr–W and W1–W2 pairs.

FIGURE 2

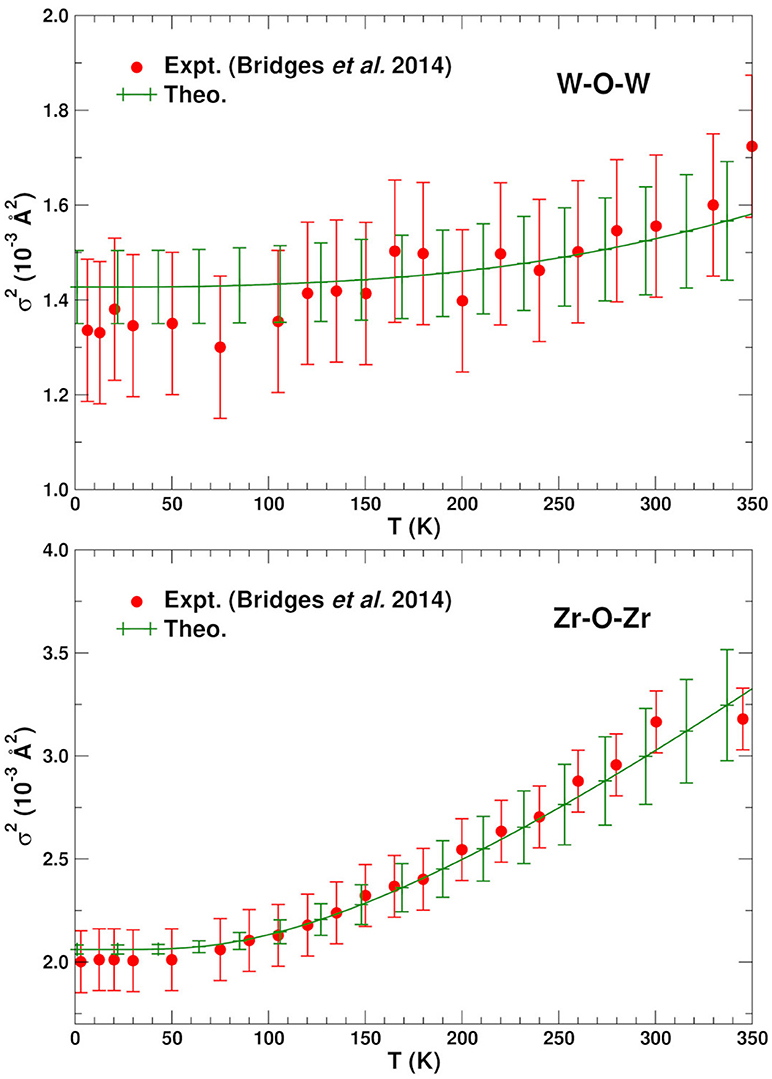
Figure 2. Comparison of the experimental (Bridges et al., 2014) and average theoretical single scattering MSRD ${\sigma }_p^2$ for the W–O–W and Zr–O–Zr in ZrW₂O₈. The theoretical values have been shifted vertically to account for experimental static disorder.

FIGURE 3

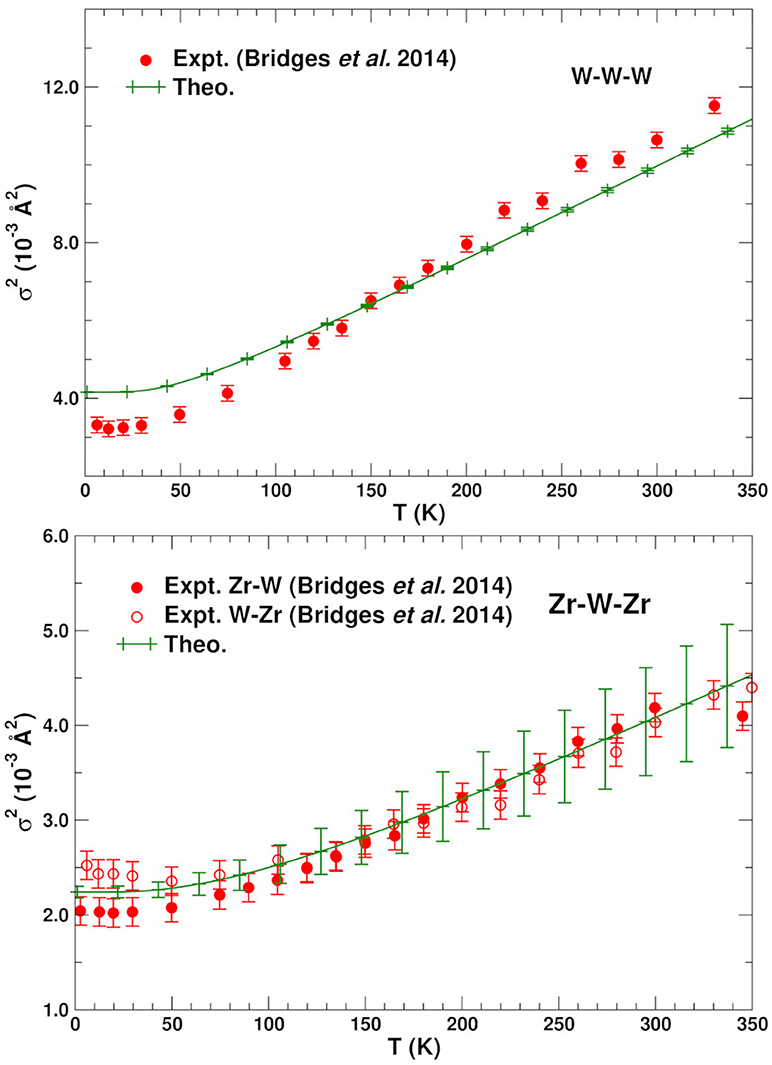
Figure 3. Comparison of the experimental (Bridges et al., 2014) and theoretical mean single scattering MSRD ${\sigma }_p^2$ for the W–W–W and Zr–W–Zr bonds in ZrW₂O₈. The theoretical values have been shifted vertically to account for experimental static disorder.

TABLE 3

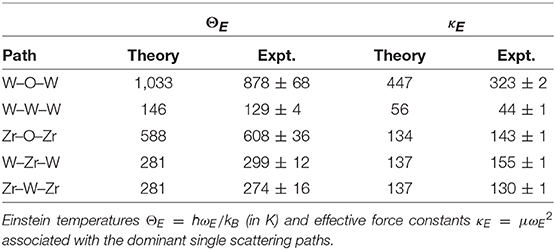
Table 3. Comparison of the theoretical and experimental (Bridges et al., 2014).

As noted above the most relevant paths for EXAFS studies of NTE are those involving the Zr and W atoms. Table 2 summarizes the structural properties of these paths, as well as their MSRDs (without static disorder corrections) at three temperatures. Note that the MSRDs for the SS and MS 173° paths are nearly identical, since they are nearly collinear and the push-pull distortions of the Zr–O and W–O bonds essentially cancel. For the 155° linkage paths, the MS MSRDs are also similar again because they involve near-neighbor bond distortions. The only exception is the Zr–W1–Zr path that is slightly softer. This path involves the nearly-independent coupling between the Zr and W atoms, which is dominated by the distortion of 2 Zr–O bonds and all 4 of the W–O bonds. This suggests that the MSRD of Zr–W1–Zr paths is larger because the W1–O1 bonds are longer, and thus weaker, than the W2–O2 ones. Figure 4 shows a comparison of the average theoretical DW factors for the Zr–W–Zr and Zr–O–W–Zr paths with experiment (Cao et al., 2003). Clearly our results match closely except at low temperature, where the experimental data also has significant errors. It is interesting to note that the larger slope for the Zr–W–Zr path arises from the Zr–W1–Zr contribution. Overall, the results in Figure 4 and Table 2 show that the length-fluctuations ${\sigma }_p^2$ of these paths are only weakly temperature dependent, and thus are “stiff,” consistent with the interpretation of Bridges et al. (2014). The stiffness of a given SS or MS path linkage is characterized by the effective spring constant κ_p for the DW factor of a given path p. It is reflected by its temperature dependence which varies as k_BT/κ_p at high T. More precisely, ${\kappa }_p={\mu }_p{{\bar{\omega }}_p}^2$ where $1/{\bar{\omega }}_p^2=\langle 1/{\omega }^2\rangle$ is the inverse 2nd moment of the PDOS. Thus the Zr–O–W linkage is considered stiff because for a large κ_p, the associated path DW factor varies weakly with temperature with a small slope 1/κ_p. Note however, that this weak temperature dependence does not preclude the existence of large transverse fluctuations of the O atoms in the linkages. Our calculations of the DM show that the transverse fluctuations perpendicular to the Zr–O–W plane have much smaller spring constants (Vila et al., 2018) and, hence, substantial larger values of u² for the O atom in the linkage (see Figure 5).

FIGURE 4

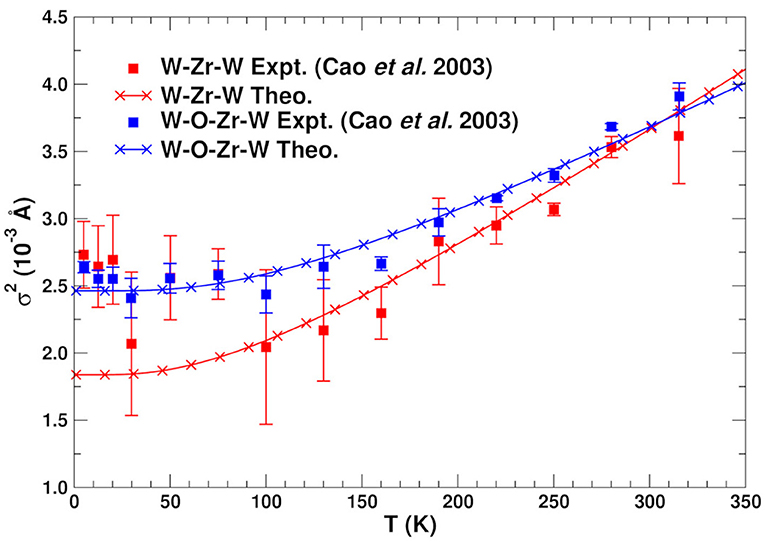
Figure 4. Comparison of the experimental (Cao et al., 2003) and theoretical MSRD σ² for the SS and MS paths associated with the Zr–W linkage in ZrW₂O₈. The theoretical values are shifted vertically to account for experimental static disorder.

FIGURE 5

Figure 5. Longitudinal and transverse MSDs u² for the O1 and O2 bridging atoms.

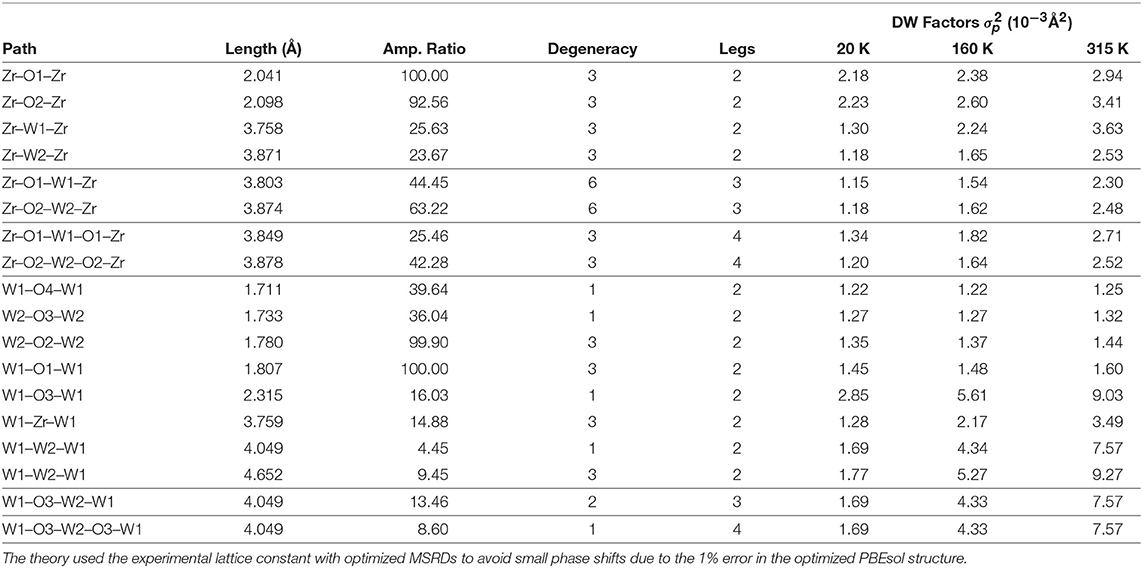
3.2. Atomic Displacements

Figure 5 shows the longitudinal and transverse mean square displacements (MSD) u² for the O1 and O2 linkage atoms. The in-plane transverse direction here is defined as the bisector of the Zr–O–W angle. The longitudinal and transverse out-of-plane directions are defined as the in- and out-of-plane perpendicular directions to this bisector, respectively. Although the 155° linkage is more asymmetric and therefore might be expected to be anisotropic, both types of linkages have similar transverse MSDs. In contrast the longitudinal motion has a relatively small, high-frequency amplitude with a large associated Einstein temperature of 600 K, as expected from the distortion along the stiff W–O and Zr–O bonds. Due to the weaker force constants associated with the bond bending (Vila et al., 2018), however, the transverse motion has an Einstein temperature of about 250 K. At T = 300 K this results in rms amplitudes u ≈ 0.12 Å. This corresponds roughly to linkage angle distortions of about δθ ≈ 6°, which are more than twice the longitudinal fluctuations at the same temperature. Although these transverse distortions are substantial, they have little effect on the bond stretching MSRDs (Poiarkova and Rehr, 1999a; Fornasini et al., 2004). For the SS paths, this is easy to see, since for a bond of length R, the perpendicular contribution from each atom is ${\sigma }_{\perp }^2~{(u^2/2R)}^2$. For the linkage bonds with R~ 2 Å and u~ 0.12 Å, we estimate that ${\sigma }_{\perp }^2~$ 0.02 × 10⁻³ Ų, which is an order of magnitude smaller than the typical error margins for the experimental MSRDs. A similar approach can be used for the multiple scattering paths, where the contributions of all atoms in the path need to be added. On the other hand the angular DW factors W_p(θ) may still contribute to the damping of the EXAFS from these paths.

In the amplitude-phase representation of EXAFS the magnitude of each path contribution is given by $\left|{\tilde{\chi }}_p(k)\right|=|f_{\text{eff}}^p/k{R}^2|$, which eliminates the oscillations and thus emphasizes the amplitudes of the various paths. Figure 6 shows the amplitudes $\left|k{\tilde{\chi }}_p(k)\right|$ for the 155 and 173° Zr–O–W linkages, including the Zr–W–Zr SS and Zr–W–O–Zr and Zr–O–W–O–Zr MS paths. Note that the amplitudes $\left|{\tilde{\chi }}_p(k)\right|$ do not include the Debye-Waller factors and thus have no temperature dependence. The Zr–W–Zr paths are not affected by the angle of the linkage for the Zr–W–O–Zr and Zr–O–W–O–Zr paths, also the amplitudes for the 173° linkage paths, are on average about twice as large as for the 155° paths. These differences are due to the angular dependence and forward scattering enhancement in $f_{\text{eff}}^p$ and are particularly strong for bond angles close to 180° and at high k.

FIGURE 6

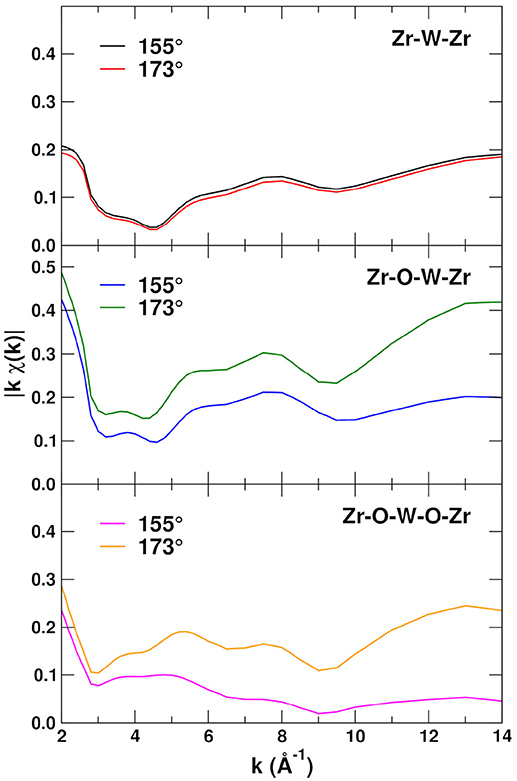
Figure 6. EXAFS path amplitudes $\left|k{\tilde{\chi }}_p(k)\right|$ for the Zr-W-Zr single-scattering and Zr-W-O-Zr and Zr-O-W-O-Zr MS paths with linkage angles 155 and 173°.

3.3. EXAFS Spectra

To assess the overall quality of our EXAFS calculations, Figure 7 shows comparisons of the experimental (Bridges et al., 2014) fine structure kχ(k) at 20, 165, and 300 K for the Zr K- and W-L₃ edges to those obtained with FEFF. The theoretical results used optimized MSRDs with bond distances reduced by 1% to correct the overestimate of the lattice constant by DFT/PBEsol calculations. Our EXAFS calculations were obtained by including all SS and MS paths of up to 5.5 Å and n_p = 4 scattering legs, and by removing all path screening filters from FEFF. The experimental results (Bridges et al., 2014) find that the many-body amplitude factor $S_0^2$ in Equation (1) is very close to 1, thus we use $S_0^2=1$ in the EXAFS simulations. Clearly the agreement is quite satisfactory for the EXAFS range k ≳ 5 Å⁻¹, below which the path expansion approach is less appropriate and atomic background substraction artifacts are possible. The small, high frequency contribution noticeable in the Zr K-edge signal at 20 K corresponds to ~ 6.5 Å Zr–Zr–Zr paths which are not included in our simulation cell.

FIGURE 7

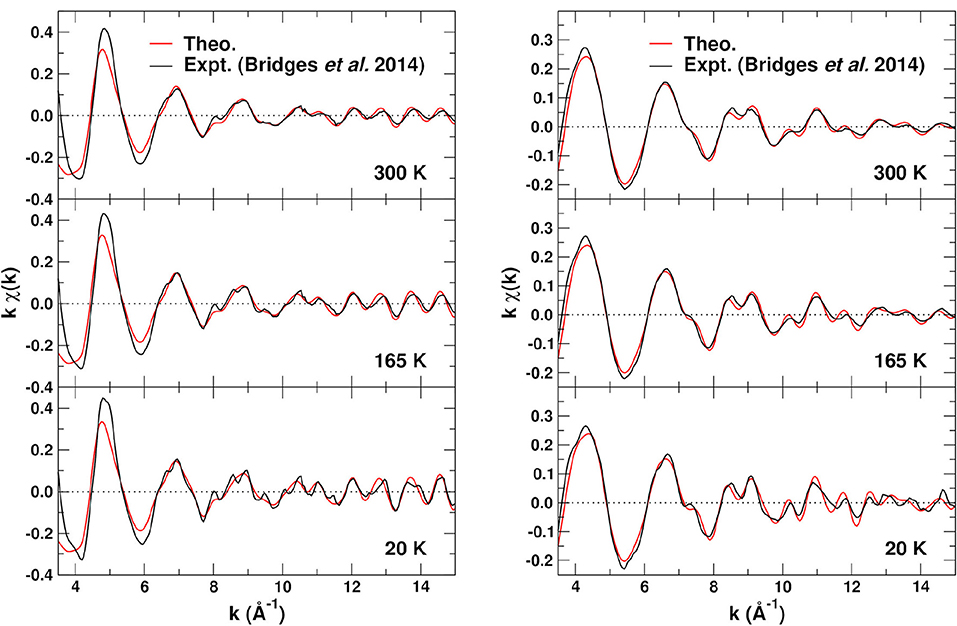
Figure 7. Comparison of the experimental (Bridges et al., 2014) and theoretical EXAFS fine structure kχ(k) at 20, 165, and 300 K for the Zr K edge (left) and the W L₃ edge (right). The theory used the experimental lattice constant with optimized MSRDs to avoid small phase shifts due to the 1% error in the optimized PBEsol structure.

Finally Figure 8 shows the phase-corrected Fourier transforms (FTs) of the kχ(k). For these transforms the central atom theoretical phase-shift 2δ_l common to all paths is subtracted before being transformed (Rehr et al., 2009), resulting in peak positions closer to their geometrical locations. Again, the overall agreement is good, except for differences in the heights of some of the peaks, due probably to static and angular disorder in the DW factors. For the Zr absorber, the FTs clearly show the Zr–O peak at about 2 Å, and the different linkage paths between 3.5 and 4.2 Å.

FIGURE 8

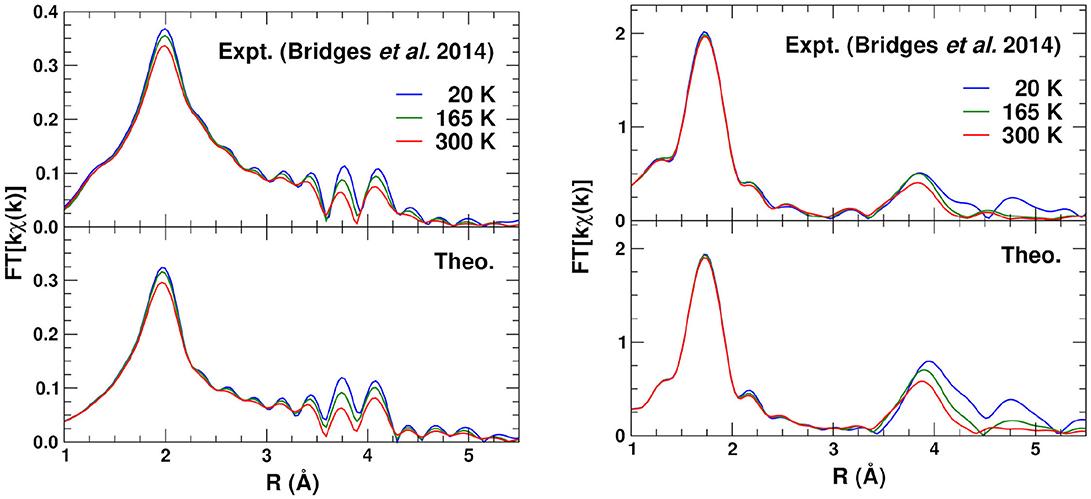
Figure 8. Comparison of the Fourier transforms of the experimental (Bridges et al., 2014) and theoretical kχ(k) (Figure 7) at 20, 165, and 300 K for the Zr K edge (left) and the W L₃ edge (right).

A potentially important issue is the effect of the Zr–O–W bond angle fluctuations during the complex low energy vibrations of the system, particularly for the Zr–O2–W2 linkage. The amplitudes of the MS peaks for the Zr–O–W linkages vary significantly with bond angle due to forward scattering through the O atom. While f_eff(θ) is strongly peaked in the forward direction and varies substantially with θ, the angular Debye-Waller factor in Equation (3) depends on the fluctuations ${\sigma }_{\theta }^2\approx 0.01$ rad². To estimate these effects we computed the average χ(k) for the Zr–O1–W1 and Zr–O2–W2 linkages over the distribution of angular distortions induced by mean u amplitues of about 0.12 Å. We find that with distortions of this amplitude the absolute change in χ(k) is only about 3 and −6% for the Zr–O1–W1 and Zr–O2–W2 linkages, respectively. This explains the good agreement between the calculations without including such averaging, and the data for the Zr edge in Figure 8. The actual situation can be more complicated, however, since the polyhedra can rotate as well as translate and a full treatment that takes this correlated motion into account would be desirable.

4. Summary and Conclusions

We have shown that theoretical calculations of structure, vibrational properties and the EXAFS of ZrW₂O₈ agree well with experiment (Bridges et al., 2014). The structural parameters are calculated using the DFT plane-wave pseudopotential VASP code with DFT/PBEsol while vibrational properties are obtained using a Lanczos algorithm and the phonon Green's function approach. The EXAFS calculations depend sensitively on these structural and vibrational properties. The fact that the calculations of the MSRDs for the most important SS and MS paths agree well show that an accurate treatment of correlated atomic motion is essential to understand the dynamic disorder. The small differences can likely be accounted for by static disorder and angular DW factors. For example, forward focusing effects in the Zr-O-W linkages are particularly important in these calculations. For example, the nearly collinear 173° paths contribute more to the amplitudes, due to enhanced forward scattering. Our calculations also show that transverse O fluctuations are substantial, consistent with results of our companion study (Vila et al., 2018), which imply that NTE is driven in part from the negative Grüneisen parameters of the low-frequency O modes. Thus while the effect of transverse fluctuations on the MSRDs is negligible, they may contribute to the angular DW factors. Our calculations also ignore anharmonic effects; although such effects are generally associated with thermal expansion (Frenkel and Rehr, 1993), this is a reasonable approximation for the dominant SS and MS paths with relatively stiff bonds. Overall our theoretical calculations yield results consistent with experiment for ZrW₂O₈ for a broad range of properties. In particular they show that both transverse motion and correlated atomic displacements are crucially important to understand the dynamic structure of this material.

Author Contributions

FV co-developed the theory, was the main developer of the specialized software used in the analysis, and performed most of the simulations. JS contributed to the initial simulations. JK performed part of the analysis (Fourier Transforms). JR co-developed the theory and contributed to the analysis. FB provided EXAFS data and contributed to the analysis.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by U.S. Department of Energy, Office of Science CSGBD Grant No. DE-FG02-03ER15476, with computational support from NERSC, a DOE Office of Science User Facility, under Contract No. DE-AC02-05CH11231. The EXAFS experiments were performed at the Stanford Synchrotron Radiation Lightsource (SSRL), which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2018.00356/full#supplementary-material

References

Auray, M., Quarton, M., and Leblanc, M. (1995). Zirconium tungstate. Acta Crystallogr. Sect. C 51, 2210–2213.

Google Scholar

Bridges, F., Keiber, T., Juhas, P., Billinge, S. J. L., Sutton, L., Wilde, J., et al. (2014). Local vibrations and negative thermal expansion in ZrW₂O₈. Phys. Rev. Lett. 112:045505. doi: 10.1103/PhysRevLett.112.045505

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, D., Bridges, F., Kowach, G. R., and Ramirez, A. P. (2002). Frustrated soft modes and negative thermal expansion in ZrW₂O₈. Phys. Rev. Lett. 89:215902. doi: 10.1103/PhysRevLett.89.215902

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, D., Bridges, F., Kowach, G. R., and Ramirez, A. P. (2003). Correlated atomic motions in the negative thermal expansion material ZrW₂O₈: a local structure study. Phys. Rev. B 68:014303. doi: 10.1103/PhysRevB.68.014303

CrossRef Full Text | Google Scholar

Deuflhard, P., and Hohmann, A. (1995). Numerical Analysis. Berlin: de Gruyter.

Google Scholar

Evans, J. S. O., David, W. I. F., and Sleight, A. W. (1999). Structural investigation of the negative-thermal-expansion material ZrW₂O₈. Acta Crystallogr. Sect. B 55, 333–340.

PubMed Abstract | Google Scholar

Fornasini, P., a Beccara, S., Dalba, G., Grisenti, R., Sanson, A., Vaccari, M., and Rocca, F. (2004). Extended x-ray-absorption fine-structure measurements of copper: local dynamics, anharmonicity, and thermal expansion. Phys. Rev. B 70:174301. doi: 10.1103/PhysRevB.70.174301

CrossRef Full Text | Google Scholar

Frenkel, A. I., and Rehr, J. J. (1993). Thermal expansion and x-ray-absorption fine-structure cumulants. Phys. Rev. B 48, 585–588.

PubMed Abstract | Google Scholar

Haydock, R. (1980). “The recursive solution of the schrodinger equation,” in Solid State Physics, Vol. 35, eds H. Ehrenreich, F. Seitz, and D. D. Turnbull (New York, NY: Academic), 215.

Google Scholar

Kresse, G., and Furthmüller, J. (1996a). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50.

Google Scholar

Kresse, G., and Furthmüller, J. (1996b). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186.

PubMed Abstract | Google Scholar

Kresse, G., and Hafner, J. (1993). Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561.

PubMed Abstract | Google Scholar

Kresse, G., and Hafner, J. (1994). Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 49, 14251–14269.

PubMed Abstract | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775.

Google Scholar

Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100:136406. doi: 10.1103/PhysRevLett.100.136406

PubMed Abstract | CrossRef Full Text | Google Scholar

Poiarkova, A. V., and Rehr, J. J. (1999a). Multiple-scattering x-ray-absorption fine-structure debye-waller factor calculations. Phys. Rev. B 59, 948–957.

Google Scholar

Poiarkova, A. V., and Rehr, J. J. (1999b). Recursion method for multiple-scattering XAFS Debye–Waller factors. J. Synchrot. Radiat. 6, 313–314.

PubMed Abstract | Google Scholar

Rehr, J. J., Kas, J. J., Prange, M. P., Sorini, A. P., Takimoto, Y., and Vila, F. (2009). Ab initio theory and calculations of X-ray spectra. Comptes Rendus Phys. 10:548–559. doi: 10.1016/j.crhy.2008.08.004

CrossRef Full Text | Google Scholar

Vila, F. D., Hayashi, S. T., and Rehr, J. J. (2018). Efficient calculation of the negative thermal expansion in ZrW₂O₈. Front. Chem. 6:296. doi: 10.3389/fchem.2018.00296

PubMed Abstract | CrossRef Full Text | Google Scholar

Vila, F. D., Rehr, J. J., Rossner, H. H., and Krappe, H. J. (2007). Theoretical x-ray absorption debye-waller factors. Phys. Rev. B 76:014301. doi: 10.1103/PhysRevB.76.014301

CrossRef Full Text | Google Scholar