- 1School of Energy and Power Engineering, Jiangsu University of Science and Technology, Zhenjiang, China
- 2School of Materials Science and Engineering, Jiangsu University of Science and Technology, Zhenjiang, China
- 3Key Laboratory of Automobile Materials, Ministry of Education, School of Materials Science and Engineering, Jilin University, Changchun, China
Polymer electrolyte membrane fuel cells (PEMFCs) are one of the most prominent clean energy technologies designed to achieve hydrogen utilization and solve problems such as low efficiency and high pollution associated with fossil fuel combustion. In order to bring about PEMFC commercialization, especially for automobile applications, developing high-activity and -selectivity catalysts for the oxygen reduction reaction (ORR) is of critical importance. Based on the density functional theory, the catalytic activity of the conductive, two-dimensional metal–organic frameworks TM3(HITP)2 monolayer (where HITP = hexaiminotriphenylene; TM = Ni, Co, Fe, Pd, Rh, Ru, Pt, Ir, and Os) for ORR has been investigated systematically. Furthermore, the classical volcano curves of the ORR activity, as a function of the OH binding, are found where the Ni, Pd, and Pt located at the weak binding side suffer from the sluggish *OOH formation and prefer the inefficient 2e− mechanism, while for other elements belonging to the strong binding side, the reactions are hindered by the poison due to ORR intermediates. Based on the free energy profiles, the corresponding overpotentials μORR exhibit the inverted volcano curve as a function of the atomic number of the 3d/4d/5d TM active center in the same period. Based on the μORR data, ORR activity decreases in the order of Ir > Co ≈ Rh > Ni ≈ Pd > Pt ≈ Fe > Ru > Os. Herein, the Co, Rh, and Ir central atoms exhibit enhanced catalytic activity in combination with the desirable selectivity of the O2 reduction to H2O. This systematic work may open new avenues for the development of high-performance non-PGM catalysts for practical applications of ORR.
Introduction
Hydrogen is a potential candidate for future energy provision, as stated in the concept of the hydrogen economy, so as to solve the issues of the rising global energy demands, depletion of fossil fuel reserves, and associated environmental pollution issues. Due to its high efficiency, ease of operation, and low emission, the polymer electrolyte membrane fuel cell (PEMFCs) is the most prominent technology to derive benefit from the proposed hydrogen cycle, which leads to the production of electricity from the electrochemical oxidation of hydrogen, with water as its endproduct (Colić and Bandarenka, 2016; Xia Z. et al., 2016; Chen et al., 2017, 2018). However, a critical obstacle to its commercialization is the dominant voltage loss associated with the sluggish oxygen reduction reaction (ORR), even when catalyzed by the noble Pt nanoparticle (Nørskov et al., 2004). In this regard, a significant amount of Pt is required to achieve the desirable power density, making the overall cost prohibitively high (Debe, 2012). In order to overcome the economic bottleneck, design, and application of earth-abundant alternatives for ORR electrocatalysis are at the heart of PEMFC research (Xia W. et al., 2016).
Inspired by the pioneering work on cobalt phthalocyanines acting as cathode catalysts (Jasinski, 1964), a tremendous amount of research is being performed on the TM–Nx carbon materials for ORR (TM denotes transition metals), especially TM–N4 active motif. The intrinsic active characteristic of TM in Nx carbon materials is experimentally supported, where the presence of the TM atom would boost the ORR performance compared with the metal-free counterpart (Peng et al., 2013; Yin et al., 2016; Yang et al., 2017); the corresponding activity would be suppressed by adding the SCN− ions and CO molecule (Zhang et al., 2016; Yang et al., 2017). Linear correlations between the content of TM–Nx and ORR activity have been observed (Yang et al., 2017). Furthermore, ORR activity shows its dependence on the TM center atom, and this is supported by the density functional theory (DFT), a theoretical work of Rossmeisl et al., where the ORR activity of the TM–N4 embedded graphene has been systematically investigated, and where the Fe, Ir, Mn, Ru, and Rh doping is identified as boosting the ORR (Calle-Vallejo et al., 2011). Additionally, the ORR mechanism is sensitive to the TM–N4 active motif. Liu et al. have synthesized the Fe–Nx and Co–Nx doped carbon nanofiber and realized that the Fe–N4 promotes 4e− ORR in comparison with the 2e− pathway of the Co–N4 one (Liu et al., 2016). The same conclusion has been achieved by Kattel et al., where the O–O bond scission is presented and the efficient 4e− reduction of O2 to 2H2O is preferred on the Fe–N4 sites, but the reduction of O2 to H2O2 is found enhanced on the Co–N4 motif (Kattel et al., 2013, 2014).
Despite these encouraging research works, such TM–N4 carbon materials generally suffer from low activity caused by the relatively few catalytic sites as well as the experimental challenge of the well-controlled active motif (Liang et al., 2013; Peng et al., 2013; Palaniselvam et al., 2016), reducing the competition with the state-of-the-art Pt/C catalysts. Paying attention to the high TM–N4 density in combination with the electronic conductivity, Miner et al. have developed the attractive Ni3(HITP)2 as ORR electrocatalyst (Miner et al., 2016). However, the performance is far from satisfying expectations, with its incomplete oxidation of O2 and the predominant production of H2O2 under the working potential (Miner et al., 2016). In this regard, utilizing the aforementioned information, the development of the efficient TM3(HITP)2 catalysts can be achieved via the variation of metal nodes (Choi et al., 2015; Zhang et al., 2015). It has naturally raised the interest to search for the optimal combinations of the TM3(HITP)2, possessing superior ORR activity as well as selectivity.
In the manuscript, DFT calculations are used within an electrochemical framework to analyze the ORR electrocatalysis over the TM3(HITP)2monolayer. In particular, the stability of the ORR intermediates is calculated, which allows to evaluate the thermodynamic ORR free energy and its overpotentials. The data provide the fundamental understanding of the mechanism of Ni3(HITP)2 and further identify optimal candidates as catalysts. According the d–partial density of states, an atomistic insight of the activity origin has been provided by a thorough comparison among the considered systems. Herein, for simplification, our attention is mainly focused on the monolayer structure shown in Figure 1 as a representative model due to the weak interaction between the interlayers of the 2D-layered materials (Sheberla et al., 2014; Chen et al., 2015; Miner et al., 2016).
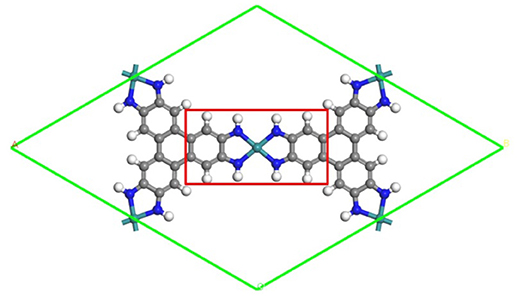
Figure 1. The schematic structure of the TM3(HITP)2 monolayer. Green, blue, gray, and white denote the TM, N, C, and H atoms.
Methods
All calculations have been performed within the DFT framework, as implemented in the DMol3 code (Delley, 1990, 2000). The generalized gradient approximation with the Perdew–Burke–Ernzerhof (PBE) functional is employed to describe exchange and correlation effects (Perdew et al., 1996). The DFT semicore pseudopotentials (DSPP) core treat method is implemented for relativistic effects, which replaces core electrons by a single effective potential and introduces some degree of relativistic correction into the core (Delley, 2002). The double numerical atomic orbital augmented by a polarization function (DNP) is chosen as the basis set (Delley, 1990). A smearing of 0.005 Ha (1 Ha = 27.21 eV) to the orbital occupation is applied to achieve accurate electronic convergence. In order to ensure high-quality results, the real-space global orbital cutoff radius is set as high as 5.2 Å. In order to accurately describe the long-range electrostatic interactions of the ORR intermediates with catalysts, the PBE-D method with the TS van der Waals (vdW) correction is employed. In the geometry optimization of structures, the convergence tolerances of energy, maximum force, and displacement are 1.0 × 10−5 Ha, 0.002 Ha/Å, and 0.005 Å, respectively. The spin-unrestricted method is used for all calculations. A conductor-like screening model (COSMO) was used to simulate a H2O solvent environment for all calculations (Todorova and Delley, 2008), which is a continuum model, where the solute molecule forms a cavity within the dielectric continuum. The DMol3/COSMO method has been generalized to periodic boundary cases. The dielectric constant is set as 78.54 for H2O. Some previous results have shown that this implicit solvation model is an effective method to describe solvation (Sha et al., 2011; Zhang et al., 2015). The 15 Å-thick vacuum is added to avoid the artificial interactions between the TM3(HITP)2 monolayer and its images. The proposed structure of the TM3(HITP)2 monolayer is shown in Figure 1, where the atoms in the red square are fixed in all of the structure-optimization calculations.
The adsorption energy (Eads) of the reactant O2 is calculated by the following,
The adsorption energy (Eads) of the ORR intermediates are calculated relative to H2O and H2 (Calle-Vallejo et al., 2011), through,
where Esys, Esubstrate, EH2O, and EH2 are the total energy of the adsorption systems, the TM3(HITP)2 monolayer, H2O molecule, and H2 molecule, respectively. The Eads < 0 corresponds to an exothermic adsorption process.
The Gibbs free energy changes (ΔG) of the ORR elemental steps have been calculated according to the computational hydrogen electrode (CHE) model developed by Nørskov et al., where the chemical potential of the proton/electron (H+ + e−) in solution is equal to the half of the chemical potential of a gas-phase H2 at the reference relative hydrogen electrode (RHE) potential (Nørskov et al., 2004). Herein, G(H++e−) = 1/2G(H2). The variance of the proton–electron pair free energy with potential is simply determined using the linear free energy dependence of the electron energy on potential, shifting the electron energy –eU, where e is the elementary positive charge and U is the electrode potential of interest on the RHE scale (Nørskov et al., 2004; Nie et al., 2014). The total chemical potential of a proton–electron pair at the potential U is written as follows:
Therefore, for a general electrochemical reaction, the free energy change ΔG for every elemental step can be determined as following:
where ΔE is the electronic energy difference based on DFT calculations, ΔZPE is the change in zero point energy, T is the temperature (equal to 298.15 K here), ΔS is the change in the entropy, and ΔGpH and ΔGU are the free energy contributions due to variation in pH value and electrode potential U, respectively. ΔGU = –eU, in which U is the potential related to the standard hydrogen electrode. ΔGpH = –kTln10 x pH, which is the corrected free energy of H+ ions depending on the concentration. According to the previous works, pH is set as 0 in acid medium and 14 in alkaline medium. The zero-point energies and entropies of the ORR intermediates are calculated from the vibrational frequencies according to standard methods. Following the suggestion of Wilcox et al. (Lim and Wilcox, 2012), in order to reduce the calculation, the TM3(HITP)2 monolayer is fully constrained. The ΔG < 0 corresponds to an exothermic adsorption process. The free energy G of O2 is derived as G(O2) = 4.92+2G(H2O)−2G(H2) by utilizing OER equilibrium at the standard conditions; the G of H2O2 is derived similarly considering that the H2O2/O2 standard equilibrium potential is 0.682 V vs. SHE (Sun et al., 2014). The CHE model has been successfully applied for developing the novel electrocatalysts with prominent ORR performances, where the DFT calculations are in line with the experimental results (Nørskov et al., 2004; Greeley et al., 2009; Favaro et al., 2015; Lang et al., 2015; Jia et al., 2016; Tang et al., 2016; Liu et al., 2017; Li et al., 2018; Xu et al., 2018). Furthermore, the PBE/DNP method in Dmol3 code has been widely employed for evaluating the potential of the TM-based carbon electrocatalysts (Wang et al., 2015, 2016b; Hou et al., 2016; Xiao et al., 2017). Therefore, the reliability of the mentioned approach is confirmed.
Results and Discussion
Prior to the investigation of the activity, the essential step is to determine the adsorption behavior of the ORR intermediates. For Ni3(HITP)2, the energetics of the O2 adsorption is endothermic with the value of 0.13 eV, caused by the structure deformation as shown in the inset of Figure 2A, indicating no such adsorption has occurred on the Ni center atom. Besides the reactant, the corresponding Eads of ORR intermediates are 4.08, 3.57, and 1.17 eV for OOH, O, and OH, respectively. In comparison with the Pt(111) (3.55 eV for OOH, 1.38 eV for O, and 0.64 eV for OH) (Xiao et al., 2016), the obviously weak adsorption ability of the center Ni atom has been observed.
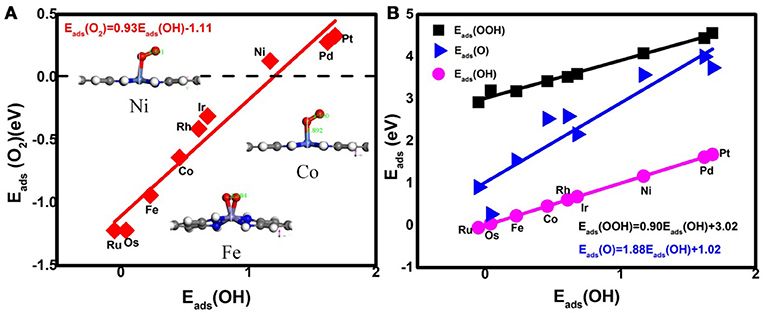
Figure 2. The adsorption energies of the O2 molecules (A) and the ORR intermediates (B). Inset: the representative O2 adsorption structure on Ni, Co, and Fe active centers.
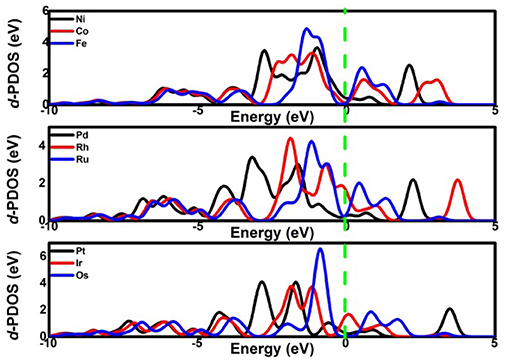
Considering the low affinity of the ORR intermediates to the Ni center, it is expected that the ORR activity would be boosted by selecting suitable TMs. Indeed, the change of the TM center definitely exhibits different adsorption behaviors, as shown in Figure 2, where the corresponding Eads data are given. From the figures, the Eads of the reactant O2 and the corresponding ORR intermediates decrease monotonically in the order of Ru ≈ Os > Fe > Co > Rh ≈ Ir > Ni > Pd ≈ Pt. It is obvious that the adsorption ability of the elements is weakened from group 8 to group 10. Carefully reviewing the O2 adsorption as shown in the inset of Figure 2A, similar to Ni, no such adsorption behaviors have occurred at the Pd and Pt active centers due to the endothermic adsorption energies. The unfavorable adsorption behavior of group 10 implies the underlying mechanism of the OOH formation, which originates from the long-range electron transfer from the catalyst to O2 molecules at the outer Helmholtz plane (Choi et al., 2014). On the contrary, group 9 binds to the reactant suitably with the corresponding end-on structure and group 8 possesses a too strong O2 adsorption with the side-on adsorption configuration. Herein, the mentioned adsorption capability is in line with the general prediction of the d-band model (Hammer and Nørskov, 2000). The corresponding evidences are provided by the d–partial density of states (d–PDOS) of the central TM atom plotted in Figure 3. As shown, the d band moves away from the Fermi energy as the TM atom changes from group 8 to group 10. The TM atom with the higher d states possesses stronger adsorption ability. Furthermore, due to the relationship between the adsorption behavior and the d band, the linear scaling relations between Eads(O2)/Eads(OOH)/Eads(O) and Eads(OH) are observed, in accordance with the previous reports of other functionalized carbon materials (Calle-Vallejo et al., 2011; Baran et al., 2014). That is,
To further evaluate the ORR activity of TM3(HITP)2, according to the experimental condition (Miner et al., 2016), the OOH associative mechanisms in the alkaline solution are taken into consideration, with the elemental steps Ri listed as follows (Wang et al., 2016a), where asterisks denote active TM sites. Due to the small barrier of proton transfer, which can be ignored at high applied voltages, our attention is only focused on the reaction energies (Nørskov et al., 2004; Calle-Vallejo et al., 2011; Zhang et al., 2015).
Analyzing the free energy plots of the complete 4e− ORR pathway in Figure 4A, the endothermic processes of *OOH formation (R1) and *O formation (R2a) are observed even at U = 0 V. The corresponding values of the free energy change ΔGi are 0.28 and 0.08 eV, respectively. The positive values indicate that the mentioned steps are thermodynamically unfavorable (Nørskov et al., 2004). When the ideal potential of 0.4 eV is applied, the mentioned reaction steps are even unfavorable with the increased ΔGi of 0.68 and 0.48 eV, respectively. Based on the information, R1 is determined as the rate-determining step (RDS), pointing to the fact that the Ni3(HITP)2 monolayer suffers from insufficient O2 activation (Greeley et al., 2009), in accordance with the endothermic capture of the O2 molecule as shown in Figure 2A. To clarify the selectivity of the 2/4e− mechanism, the comparison between R2a and R2b is considered. In the alternative 2e− pathway, the ΔG2b of the H2O2 formation (R2b) is increased from 0.01 to 0.41 eV as the U ranged from 0 to 0.4 V, being 0.07 eV lower than ΔG2a, indicating the slightly energy favorable condition of R2b. Herein, the predominant production of H2O2 would be expected on the Ni3(HITP)2 monolayer, which is in consistence with the experiment results of the 3D Ni3(HITP)2. In summary, the Ni3(HITP)2 monolayer slightly prefers the 2e− mechanism, with the RDS located at the *OOH formation.
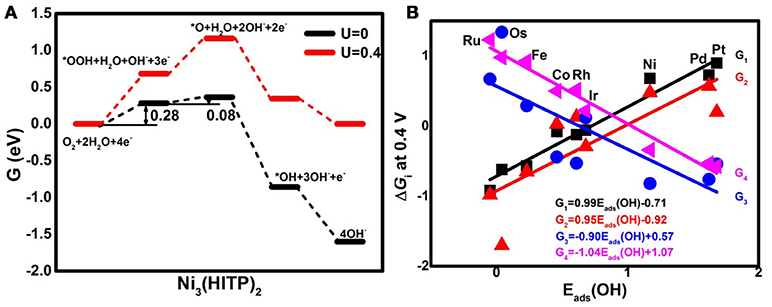
Figure 4. The free energy G diagrams of Ni3(HITP)2 in the alkaline medium (A) and the free energy change ΔGi of the elemental step Ri at the ideal potential of 0.4 eV (B).
Owing to the different adsorption abilities of TM3(HITP)2, the suitable TM would boost the ORR activity as well as the selectivity of the 4e− mechanism. In order to characterize the relationship between the ORR activity and the TM center atom, the reactive free energy change ΔGi of the elementary steps Ri at U = 0.4 V as a function of Eads(OH) is plotted in Figure 4B. As the weakening of the Eads(OH) occurs with the values ranging from −0.05 to 1.68 eV, ΔG1 and ΔG2a increase from the negative to the positive values, while the opposite tendency is found for ΔG3 and ΔG4, which decrease from the positive to the negative values. That is, the steps R1 and R2a change from the exothermic to endothermic process, while the steps R3 and R4 become more thermodynamically favorable. Obviously, the RDS steps are identified as R4 for group 8 and group 9 with the exception of Os, where the RDS step is R3, while the RDS step is located at R1 for group 10.
On the basis of the assumption that the activation barrier for the RDS is equal to ΔGmax, the activity variation of TM3(HITP)2 referred to as Ni3(HITP)2 is estimated by the rate constant k via the simple Arrhenius equation in the following,
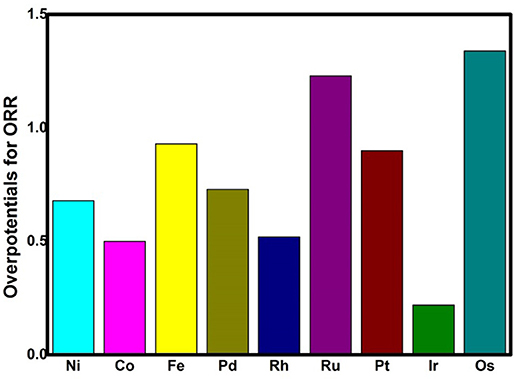
where A is the prefactor, kB is the Boltzmann constant, and T is the temperature (298.15 K). The classic volcano curve is observed in Figure 5A, where the In(kTM/kNi) as a function of the Eads(OH) is plotted. Based on our results, the adsorption ability is weakened as the atomic number increases from group 8 to group 10. The Ni/Pd/Pt active centers suffer from the too weak binding strength, leading to the energetically unfavorable process of the *OOH formation. Meanwhile, for the Fe/Ru/Os active centers, the too strong interaction with the ORR intermediates accounts for the poisoning of the O-containing intermediates. The suitable binding strength of Co/Rh/Ir active centers indicates the balance between the O2 activation and the catalyst recovery. As discussed by the previous reports (Calle-Vallejo et al., 2011; Viswanathan et al., 2012a; Baran et al., 2014; Zhang et al., 2015), the ORR activity depends on the adsorption of the intermediates. Our results are in accordance with the previous reports in that the bond strength should be compromised in the case of the effective ORR catalysts on the basis of Sabatier principle (Greeley et al., 2009; Gao et al., 2017, 2018); this is similar with the previous studies on metal (Stephens et al., 2012), functional graphene (Calle-Vallejo et al., 2011), metal porphyrine (Baran et al., 2014) as well as the 2D MOF (Gao et al., 2017). Herein, in comparison with the Ni3(HITP)2 monolayer (0.68 eV), group 9 possesses superior catalytic performance with the smaller ΔGmax of 0.50, 0.52, and 0.22 eV for the Co, Rh, and Ir center atoms, respectively. By contrast, inferior activities are observed for group 8 and group 10. The corresponding ΔGmax are 0.93, 1.23, and 1.34 eV for Fe, Ru, and Os atoms, and 0.72 and 0.90 eV for Pd and Pt atoms, respectively. Furthermore, for clarification, the data of the relative overpotentials μORR are summarized and collected for the activity comparison, depicted in Figure 6. As the atomic number of TM increased from Ni to Fe, the μORR reduces and then increases, presenting further evidence to the presence of the classical volcano-shaped activity (Nørskov et al., 2004; Calle-Vallejo et al., 2011; Baran et al., 2014; Zheng et al., 2017). Similar situations are found for the 4d/5d TM3(HITP)2 monolayer. Based on the μORR data, ORR activity decreases in the order of Ir > Co ≈ Rh > Ni ≈ Pd > Pt ≈ Fe > Ru > Os. Furthermore, compared with the data of the TM supported on graphene and macrocyclic molecules (the minimum μORR = 0.4 eV) (Xu et al., 2018), the prominent improvement of the ORR activity on the Ir3(HITP)2 monolayer is confirmed.
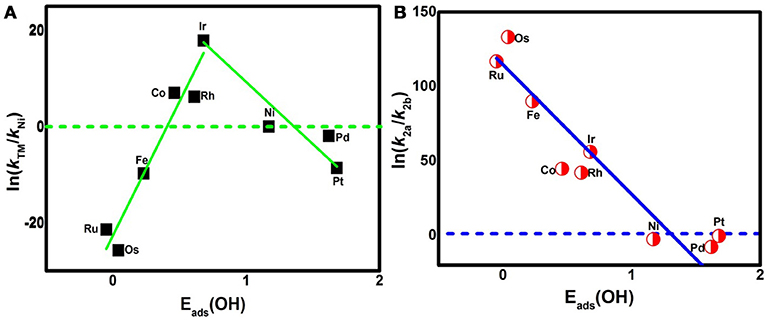
Figure 5. The activity enhancement factor of TM3(HITP)2 referred to the Ni3(HITP)2 (A) and the selectivity of the 4e− reduction referred to the 2e− pathway (B).
Besides the ORR activity, the ORR selectivity is characterized by the ratio of the corresponding reaction rate k2a (k2b) for step R2a (R2b), via the following equation,
The data are plotted in Figure 5B. As shown, In(k2a/k2b) shows a linear relationship with Eads(OH). For the weak side, the values of ΔG2a and ΔG2b are 0.48 and 0.41 eV for Ni, 0.57 and 0.37 eV for Pd, and 0.20 and 0.19 eV for Pt, respectively. The corresponding In(k2a/k2b) are −2.72, −7.78, and −0.39, indicating the energy favorability of R2b compared with that of R2a for group 10. Furthermore, considering the In(k2a/k2b) data, the 2e− reduction of O2 to H2O2 is prevalent at the Ni and Pd centers, while the mixing of 2/4e− ORR is reasonable for the Pt center. By contrast, R2a is preferred for other elements indicated by the positive In(k2a/k2b). That is, the 4e− mechanism is dominant for group 8 and group 9. Obviously, as the Eads(OH) is strengthened, the catalytic selectivity is changed from the 2e− to 4e− pathway. The two sides of the catalytic activity profile shown in Figure 5A essentially distinguish the 2e− catalysts (weak binding side) from the 4e− catalysts (strong binding side) (Viswanathan et al., 2012b; Zagal and Koper, 2016). That is, the former suffering from the insufficient O2 activation favors the H2O2 formation; the latter poisoned by the O–containing intermediates generally prefers the H2O formation. The formation of H2O2 not only decreases the ORR efficiency, but also degrades the proton exchange membrane (Tsuneda et al., 2017). In short, the dramatic enhancements in oxygen-reduction rates and product selectivity are achieved by selecting TM centers in group 9, in line with the previous works (Gao et al., 2017; Wannakao et al., 2017).
To understand the influence of the long-term electrostatic potential on the ORR performance, the vdW correction is further applied for analyzing the optimum Ir/Co/Rh systems, where the corresponding adsorption energy and the free energy changes are listed in Table 1. Intuitively, the adsorption abilities of the mentioned systems are enhanced due to the presence of the long-term interaction, in consistence with our calculation data. For the Ir3(HITP)2 monolayer, the Eads are slightly increased to −0.39, 3.49, 2.11, and 0.61 eV for O2, OOH, O, and OH, respectively, in comparison with the uncorrected values of −0.31, 3.59, 2.16, and 0.68 eV. The perturbation of the binding strength hinders the OH removal from the Ir active site, leading to the uphill of the ΔGmax from 0.22 to 0.30 eV. Despite the activity decrease, the 4e− reduction pathway remains, supported by the values of ΔG2a with −0.23 eV and ΔG2b with 1.26 eV. Herein, the same phenomenon is found for Co3(HITP)2 and Rh3(HITP)2 with the ΔGmax of 0.68 and 0.59 eV, respectively. The corresponding ORR activity with th 4e− reaction mechanism follows the order of Ir > Rh ≈ Co. Despite the numerical variation, the trend is roughly consistent with the results without considering vdW interaction.
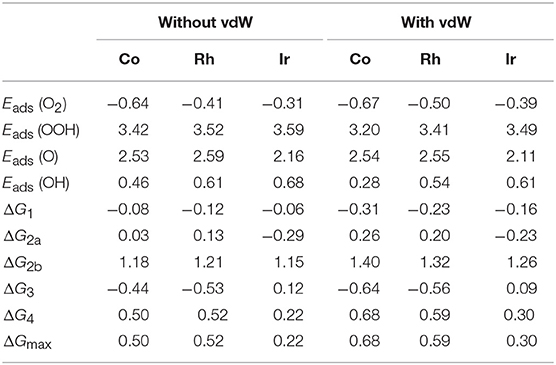
Table 1. The Eads and ΔG of ORR intermediates at the potential U = 0.4V with and without the vdW corrections.
Despite the presence of the Ni3(HITP)2 experimentally, other 2D catalysts are only theoretical models, which need the confirmation of their synthesis. It should be noted that changing metal atoms would significantly modify the corresponding structures. Thus, by replacing the Ni central atom, the dimensionality of the Cr3(HITP)2 could be transferred from 2D to 3D due to the energetic favorable insertion of the spacer linker (Foster et al., 2016). Different structures inevitably lead to distinct catalytic performances (Sun et al., 2014). In this regard, although the theoretical candidates have been rationally predicted, the ORR performance of the optimum TM3(HITP)2 with the Co/Rh/Ir active sites crucially needs further experimentally verification.
Conclusion
Based on the DFT, the ORR mechanisms on TM3(HITP)2 monolayer have been studied. It is found that the selection of central metals affects the adsorption behaviors, tuning ORR activity and its selectivity. It is realized that the adsorption abilities are monotonously enhanced as the d band upshifts from group 10 to group 8. A classical volcano relationship for the predicted ORR activity as a function of calculated OH adsorption energy is observed. From the calculated ΔG data, the ORR activity decreases in the order of Ir > Co ≈ Rh > Ni ≈ Pd > Pt ≈ Fe > Ru > Os. That is, group 9 possesses superior activity compared with other elements. Furthermore, owing to the insufficient O2 activation, the 2e− mechanism is prevalent in group 10, while the desirable 4e− mechanism is dominant for others. These results would throw insights into the nature of the ORR mechanisms of TM3(HITP)2. The materials of the Co3(HITP)2, Rh3(HITP)2, and Ir3(HITP)2 have been screened out and served as the potential candidates for the ORR electrocatalysis.
Author Contributions
BX carried out the simulation and wrote the paper. QJ revised the paper. HZ, HL, and XJ entered the discussion. All authors commented on the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge the support from the National Natural Science Foundation of China (No. 21503097, 51631004) and the Natural Science Foundation of Jiangsu (No.BK20140518).
References
Baran, J. D., Grönbeck, H., and Hellman, A. (2014). Analysis of porphyrines as catalysts for electrochemical reduction of O2 and oxidation of H2O. J. Am. Chem. Soc. 136, 1320–1326. doi: 10.1021/ja4060299
Calle-Vallejo, F., Martinez, J. I., and Rossmeisl, J. (2011). Density functional studies of functionalized graphitic materials with later transition metals for oxygen reduction reaction. Phys. Chem. Chem. Phys. 13, 15639–15643. doi: 10.1039/c1cp21228a
Chen, D., Xu, Y., Hu, B., Yan, C., and Lu, L. (2018). Investigation of proper external air flow path for tubular fuel cell stacks with an anode support feature. Energ. Convers. Manage. 171, 807–814. doi: 10.1016/j.enconman.2018.06.036
Chen, D., Xu, Y., Tade, M. O., and Shao, Z. (2017). General regulation of air flow distribution characteristics within planar solid oxide fuel cell stacks. ACS Energy Lett. 2, 319–326. doi: 10.1021/acsenergylett.6b00548
Chen, S., Dai, J., and Zeng, X. C. (2015). Metal–organic kagome lattices M3(2,3,6,7,10, 11-hexaiminotriphenylene)2 (M = Ni and Cu): from semiconducting to metallic by metal substitution. Phys. Chem. Chem. Phys. 17, 5954–5958. doi: 10.1039/C4CP05328A
Choi, C. H., Lim, H. K., Chung, M. W., Park, J. C., Shin, H., Kim, H., et al. (2014). Long-range electron transfer over graphene-based catalyst for high-performing oxygen reduction reactions: importance of size, N-doping, and metallic impurities. J. Am. Chem. Soc. 136, 9070–9077. doi: 10.1021/ja5033474
Choi, W. I., Wood, B. C., Schwegler, E., and Ogitsu, T. (2015). Combinatorial search for high-activity hydrogen catalysts based on transition-metal-embedded graphitic carbons. Adv. Energy. Mater. 5:1501423. doi: 10.1002/aenm.201501423
Colić, V., and Bandarenka, A. S. (2016). Pt alloy electrocatalysts for oxygen reduction reaction: from model surfaces to nanostructured systems. ACS Catal. 6, 5378–5385. doi: 10.1021/acscatal.6b00997
Debe, M. K. (2012). Electrocatalyst approaches and challenges for automotive fuel cells. Nature 486, 43–51. doi: 10.1038/nature11115
Delley, B. (1990). An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys. 92, 508–517. doi: 10.1063/1.458452
Delley, B. (2000). From molecules to solids with the DMol3 approach. J. Chem. Phys. 113, 7756–7764. doi: 10.1063/1.1316015
Delley, B. (2002). Hardness conserving semilocal pseudopotentials. Phys. Rev. B 66:155125. doi: 10.1103/PhysRevB.66.155125
Favaro, M., Ferrighi, L., Fazio, G., Colazzo, L., Di Valentin, C., Durante, C., et al. (2015). Single and multiple doping in graphene quantum dots: unraveling the origin of selectivity in the oxygen reduction reaction. ACS Catal. 5, 129–144. doi: 10.1021/cs501211h
Foster, M. E., Sohlberg, K., Spataru, C. D., and Allendorf, M. D. (2016). Proposed modification of the graphene analogue Ni3(HITP)2 to yield a semiconducting material. J. Phys. Chem. C 120, 15001–15008. doi: 10.1021/acs.jpcc.6b05746
Gao, G., Bottle, S., and Du, A. (2018). Understanding the activity and selectivity of single atom catalysts for hydrogen and oxygen evolution via ab initial study. Catal. Sci. Technol. 8, 996–1001. doi: 10.1039/C7CY02463K
Gao, G., Waclawik, E. R., and Du, A. (2017). Computational screening of two-dimensional coordination polymers as efficient catalysts for oxygen evolution and reduction reaction. J. Catal. 352, 579–585. doi: 10.1016/j.jcat.2017.06.032
Greeley, J., Stephens, I. E. L., Bondarenko, A. S., Johansson, T. P., Hansen, H. A., Jaramillo, T. F., et al. (2009). Alloys of platinum and early transition metals as oxygen reduction electrocatalysts. Nat. Chem. 1, 552–556. doi: 10.1038/nchem.367
Hammer, B., and Nørskov, J. K. (2000). Theoretical surface science and catalysis-calculations and concepts. Adv. Catal. 45, 71–129. doi: 10.1016/S0360-0564(02)45013-4
Hou, X., Zhang, P., Li, S., and Liu, W. (2016). Enhanced electrocatalytic activity of nitrogen-doped olympicene/graphene hybrids for the oxygen reduction reaction. Phys. Chem. Chem. Phys. 18, 22799–22804. doi: 10.1039/C6CP03451A
Jasinski, R. (1964). A new fuel cell cathode catalyst. Nature 201, 1212–1213. doi: 10.1038/2011212a0
Jia, Y., Zhang, L., Du, A., Gao, G., Chen, J., Yan, X., et al. (2016). Defect graphene as a trifunctional catalyst for electrochemical reactions. Adv. Mater. 28, 9532–9538. doi: 10.1002/adma.201602912
Kattel, S., Atanassov, P., and Kiefer, B. (2013). Catalytic activity of Co-Nx/C electrocatalysts for oxygen reduction reaction: a density functional theory study. Phys. Chem. Chem. Phys. 15, 148–153. doi: 10.1039/C2CP42609A
Kattel, S., Atanassov, P., and Kiefer, B. (2014). A density functional theory study of oxygen reduction reaction on non-PGM Fe-Nx-C electrocatalysts. Phys. Chem. Chem. Phys. 16, 13800–13806. doi: 10.1039/c4cp01634c
Lang, X. Y., Han, G. F., Xiao, B. B., Gu, L., Yang, Z. Z., Wen, Z., et al. (2015). Mesostructured intermetallic compounds of platinum and non-transition metals for enhanced electrocatalysis of oxygen reduction reaction. Adv. Funct. Mater. 25, 230–237. doi: 10.1002/adfm.201401868
Li, F., Han, G. F., Noh, H. J., Kim, S.-J., Lu, Y., Jeong, H. Y., et al. (2018). Boosting oxygen reduction catalysis with abundant copper single atom active sites. Energy Environ. Sci. 11, 2263–2269. doi: 10.1039/C8EE01169A
Liang, H. W., Wei, W., Wu, Z.-S., Feng, X., and Müllen, K. J. (2013). Mesoporous metal-nitrogen-doped carbon electrocatalysts for highly efficient oxygen reduction reaction. J. Am. Chem. Soc. 135, 16002–16005. doi: 10.1021/ja407552k
Lim, D. H., and Wilcox, J. (2012). Mechanisms of the oxygen reduction reaction on defective graphene-supported Pt nanoparticles from first-principles. J. Phys. Chem. C 116, 3653–3660. doi: 10.1021/jp210796e
Liu, J., Jiao, M., Lu, L., Barkholtz, H. M., Li, Y., Wang, Y., et al. (2017). High performance platinum single atom electrocatalyst for oxygen reduction reaction. Nat. Commun. 8:15938. doi: 10.1038/ncomms15938
Liu, K., Kattel, S., Mao, V., and Wang, G. (2016). Electrochemical and computational study of oxygen reduction reaction on nonprecious transition metal/nitrogen doped carbon nanofibers in acid medium. J. Phys. Chem. C 120, 1586–1596. doi: 10.1021/acs.jpcc.5b10334
Miner, E. M., Fukushima, T., Sheberla, D., Sun, L., Surendranath, Y., and Dincă, M. (2016). Electrochemical oxygen reduction catalysed by Ni3(hexaiminotriphenylene)2. Nat. Commun. 7:10942. doi: 10.1038/ncomms10942
Nie, X., Luo, W., Janik, M. J., and Asthagiri, A. (2014). Reaction mechanisms of CO2 electrochemical reduction on Cu (1 1 1) determined with density functional theory. J. Catal. 312, 108–122. doi: 10.1016/j.jcat.2014.01.013
Nørskov, J. K., Rossmeisl, J., Logadottir, A., Lindqvist, L., Kitchin, J. R., Bligaard, T., et al. (2004). Origin of the overpotential for oxygen reduction at a fuel–cell cathode. J. Phys. Chem. B 108, 17886–17892. doi: 10.1021/jp047349j
Palaniselvam, T., Kashyap, V., Bhange, S. N., Baek, J. B., and Kurungot, S. (2016). Nanoporous graphene enriched with Fe/Co-N active sites as a promising oxygen reduction electrocatalyst for anion exchange membrane fuel cells. Adv. Funct. Mater. 26, 2150–2162. doi: 10.1002/adfm.201504765
Peng, H., Mo, Z., Liao, S., Liang, H., Yang, L., Luo, F., et al. (2013). High performance Fe- and N- doped carbon catalyst with graphene structure for oxygen reduction. Sci. Rep. 3:1765. doi: 10.1038/srep01765
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi: 10.1103/PhysRevLett.77.3865
Sha, Y., Yu, T. H., Merinov, B. V., Shirvanian, P., and Goddard, W. A. (2011). Oxygen hydration mechanism for the oxygen reduction reaction at Pt and Pd fuel cell catalysts. J. Phys. Chem. Lett. 2, 572–576. doi: 10.1021/jz101753e
Sheberla, D., Sun, L., Blood-Forsythe, M. A., Er, S., Wade, C. R., Brozek, C. K., et al. (2014). High electrical conductivity in Ni3(2,3,6,7,10,11-hexaiminotriphenylene)2, a semiconducting metal-organic graphene analogue. J. Am. Chem. Soc. 136, 8859–8862. doi: 10.1021/ja502765n
Stephens, I. E. L., Bondarenko, A. S., Grønbjerg, U., Rossmeisl, J., and Chorkendorff, I. (2012). Understanding the electrocatalysis of oxygen reduction on platinum and its alloys. Energy Environ. Sci. 5, 6744–6762. doi: 10.1039/C2EE03590A
Sun, J., Fang, Y., and Liu, Z. (2014). Electrocatalytic oxygen reduction kinetics on Fe-center of nitrogen-doped graphene. Phys. Chem. Chem. Phys. 16, 13733–13740. doi: 10.1039/C4CP00037D
Tang, C., Wang, H. F., Chen, X., Li, B. Q., Hou, T. Z., Zhang, B., et al. (2016). Topological defects in metal-free nanocarbon for oxygen electrocatalysis. Adv. Mater. 28, 6845–6851. doi: 10.1002/adma.201601406
Todorova, T., and Delley, B. (2008). Wetting of paracetamol surfaces studied by DMol3-COSMO calculations. Mol. Simul. 34, 1013–1017. doi: 10.1080/08927020802235672
Tsuneda, T., Singh, R. K., Iiyama, A., and Miyatake, K. (2017). Theoretical Investigation of the H2O2-Induced Degradation Mechanism of Hydrated Nafion Membrane via Ether-Linkage Dissociation. ACS Omega 2, 4053–4064. doi: 10.1021/acsomega.7b00594
Viswanathan, V., Hansen, H. A., Rossmeisl, J., and Nørskov, J. K. (2012a). Universality in oxygen reduction electrocatalysis on metal surfaces. ACS Catal. 2, 1654–1660. doi: 10.1021/cs300227s
Viswanathan, V., Hansen, H. A., Rossmeisl, J., and Nørskov, J. K. (2012b). Unifying the 2e− and 4e− reduction of oxygen on metal surfaces. J. Phys. Chem. Lett. 3, 2948–2951. doi: 10.1021/jz301476w
Wang, N., Feng, L., Shang, Y., Zhao, J., Cai, Q., and Jin, P. (2016a). Two-dimensional iron-tetracyanoquinodimethane(Fe-TCNQ) monolayer: an efficient electrocatalysts for the oxygen reduction reaction. RSC Adv. 6, 72952–72958. doi: 10.1039/C6RA14339C
Wang, N., Liu, Y., Zhao, J., and Cai, Q. (2016b). DFT-based study on the mechanisms of the oxygen reduction reaction on Co(acetylacetonate)2 supported by N-doped graphene nanoribbon. RSC Adv. 6, 79662–79667. doi: 10.1039/C6RA17651H
Wang, Y., Yuan, H., Li, Y., and Chen, Z. (2015). Two-dimensional iron-phthalocyanine (Fe-Pc) monolayer as a promising single-atom-catalyst for oxygen reduction reaction: a computational study. Nanoscale 7, 11633–11641. doi: 10.1039/C5NR00302D
Wannakao, S., Maihom, T., Kongpatpanich, K., Limtrakul, J., and Promarak, V. (2017). Halogen substitutions leading to enhanced oxygen evolution and oxygen reduction reactions in metalloporphyrin frameworks. Phys. Chem. Chem. Phys. 19, 29540–29548. doi: 10.1039/C7CP06187K
Xia, W., Mahmood, A., Liang, Z., Zou, R., and Guo, S. (2016). Earth-abundant nanomaterials for oxygen reduction. Angew. Chem. Int. Ed. 55, 2650–2676. doi: 10.1002/anie.201504830
Xia, Z., An, L., Chen, P., and Xia, D. (2016). Non-Pt nanostructured catalysts for oxygen reduction reaction: synthesis, catalytic activity and its key factors. Adv. Energy Mater. 6:1600458. doi: 10.1002/aenm.201600458
Xiao, B. B., Jiang, X. B., and Jiang, Q. (2016). Density functional theory study of oxygen reduction reaction on Pt/Pd3Al(111) alloy electrocatalyst. Phys. Chem. Chem. Phys. 18, 14234–14243. doi: 10.1039/C6CP01066K
Xiao, B. B., Liu, H. Y., Jiang, X. B., Yu, Z. D., and Jiang, Q. (2017). A bifunctional two dimensional TM3(HHTP)2 monolayer and its variations for oxygen electrode reactions. RSC Adv. 7, 54332–54340. doi: 10.1039/C7RA09974F
Xu, H., Cheng, D., Cao, D., and Zeng, X. C. (2018). A universal principle for a rational design of single-atom electrocatalysts. Nat. Catal. 1, 339–348. doi: 10.1038/s41929-018-0063-z
Yang, X., Zheng, Y., Yang, J., Shi, W., Zhong, J. H., Zhang, C., et al. (2017). Modeling Fe/N/C catalysts in monolayer graphene. ACS Catal. 7, 139–145. doi: 10.1021/acscatal.6b02702
Yin, P., Yao, T., Wu, Y., Zheng, L., Lin, Y., Liu, W., et al. (2016). Single cobalt atoms with precise N-coordination as superior oxygen reduction reaction catalysts. Angew. Chem. Int. Ed. 55, 10800–10805. doi: 10.1002/anie.201604802
Zagal, J. H., and Koper, M. (2016). Reactivity descriptors for the activity of molecular MN4 catalysts for the oxygen reduction reaction. Angew. Chem. Int. Ed. 55, 14510–14521. doi: 10.1002/anie.201604311
Zhang, P., Hou, X., Liu, L., Mi, J., and Dong, M. (2015). Two-dimensional π-conjugated metal bis(dithiolene) complex nanosheets as selective catalysts for oxygen reduction reaction. J. Phys. Chem. C 119, 28028–28037. doi: 10.1021/acs.jpcc.5b09148
Zhang, Q., Mamtani, K., Jain, D., Ozkan, U., and Asthagiri, A. (2016). CO poisoning effects on FeNC and CNx ORR catalysts: a combined experimental-computational study. J. Phys. Chem. C 120, 15173–15184. doi: 10.1021/acs.jpcc.6b03933
Keywords: oxygen reduction reaction, activity and selectivity, 2D materials, transition metal elements, DFT calculation
Citation: Xiao B, Zhu H, Liu H, Jiang X and Jiang Q (2018) The Activity Improvement of the TM3(hexaiminotriphenylene)2 Monolayer for Oxygen Reduction Electrocatalysis: A Density Functional Theory Study. Front. Chem. 6:351. doi: 10.3389/fchem.2018.00351
Received: 19 May 2018; Accepted: 25 July 2018;
Published: 12 September 2018.
Edited by:
Zhimin Ao, Guangdong University of Technology, ChinaReviewed by:
Aijun Du, Queensland University of Technology, AustraliaSimonetta Antonaroli, Università degli Studi di Roma Tor Vergata, Italy
Copyright © 2018 Xiao, Zhu, Liu, Jiang and Jiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Beibei Xiao, eGlhb2JiMTFAbWFpbHMuamx1LmVkdS5jbg==
Qing Jiang, amlhbmdxQGpsdS5lZHUuY24=
 Beibei Xiao
Beibei Xiao Hui Zhu1
Hui Zhu1