
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Built Environ. , 28 April 2020
Sec. Earthquake Engineering
Volume 6 - 2020 | https://doi.org/10.3389/fbuil.2020.00050
This article is part of the Research Topic Recent Advances and Applications of Seismic Isolation and Energy Dissipation Devices View all 19 articles
This paper analyses the new Research Centre designed for the University of Camerino and entirely financed by the national Civil Protection Department (DPC), following the seismic events in Central Italy in 2016. The building has been designed to guarantee speed of execution as well as a high level of safety, especially regarding seismic actions. The structural solution was to create an isolated system with a steel braced super-structure with pinned joints and r.c. sub-structures able to adapt to the complex morphology of the area. As described in the first part of the paper, design choices have been made to achieve a high level of resilience and robustness, i.e., to limit damage to structural and non-structural components and equipment under moderate and design seismic actions and to avoid disproportionate consequences in the event of extreme actions, larger than the design ones. In the second part of the paper, specific risk analyses have been carried out to evaluate the real performance of the building under increasing intensity levels, with reference to both serviceability and ultimate conditions. To this purpose a site-specific hazard study was first conducted, then non-linear analyses were performed using a hazard-consistent set of records with return periods ranging from TR = 60 years to TR = 10000 years. The main demand parameters of both the isolation system and the super-structure were recorded and capacity values corresponding to different ultimate and damage limit conditions were defined. The results obtained in terms of demand hazard curves show that the building performances in terms of robustness and resilience are very high, confirming the efficacy of the strategies adopted in the design.
Since the seismic events in Central Italy in 2016, which severely damaged the city of Camerino, several buildings are under reconstruction or are to be rebuilt. One of these is the new University of Camerino Research Centre, which is entirely financed by the national Civil Protection Department (DPC). The structure, as required by the funding body, was conceived by privileging solutions guaranteeing the speed of execution (and possible dismantling) and a high level of safety, especially with regard to seismic actions.
The structural solution was therefore to create an isolated system with a steel braced super-structure with pinned joints and r.c. sub-structures able to adapt to the complex morphology of the area. In particular, a hybrid isolation system was adopted, comprising High Damping Rubber (HDR) bearings and low-friction sliders able to provide a high period of isolation. The choice of this isolation system is mainly due to their good behavior for both low-medium and strong intensity earthquakes. In fact, the hazard of the site does not lead to excessive displacements for strong earthquakes, which can be faced with a moderate damping. Thus, high dissipative solutions, such as lead rubber bearings (LRBs) or curved surface sliders (CSSs) are not required in this case. Moreover, the solution with HDR bearings is better in providing resilience to the building for frequent earthquakes, i.e., no damage or downtime. In fact, for lower displacements the stiffness and damping of this kind of bearings only slightly increase. Differently, devices such LRBs or CSSs are characterized by high level of damping and stiffness for small displacements, which could lead to larger floor accelerations for frequent events (Yang et al., 2010). This would be very dangerous for the Research Centre object of this paper, given the potentially high risk activities in the chemistry and physics laboratories, where dangerous substances and expensive equipment sensitive to floor accelerations will be housed. Moreover, since the building is intended for public use with the possibility of accommodating large crowds and may even be used as coordination center in the organization of civil protection post-earthquake activities in the case of possible future seismic events, two complementary strategies have been adopted to also ensure adequate structural robustness against extreme actions, larger than the design ones. The first consists of a safety margin adopted for the displacement capacity of both the devices composing the isolation system and the seismic gaps on the upstream side of the building. For both of them a capacity limit greater than the maximum design displacement at the Collapse Limit State (CLS, characterized by the return period of TR = 950 years) has been required to avoid anomalous behaviors, such as the exit of the sliders out of the sliding surface or the impact of the building with neighboring structures. The second strategy consists of adopting a steel super-structure equipped with elasto-plastic braces, able to limit disproportionate consequences in the case of even more large horizontal actions. This aspect is guaranteed by the over-strength of the diagonal brace, which is important in the case of extreme horizontal actions causing an increase in the stiffness of the HDR bearings (due to their hardening behavior) or the closure of the gaps. Finally, the robustness under exceptional scenario (such as fire events or explosions) leading to the loss of vertical bearing of isolators is ensured by adopting safety supports around the device.
In this paper a description of the building is first presented, then the design procedure of the base-isolated building is illustrated and finally a specific risk analysis is reported to demonstrate the achievement of the design objectives, i.e., a very low seismic risk in terms of the attainment of both damage and ultimate limit states. In particular, the last part of the paper reports a site-specific hazard study carried out with the Reasses v.2.0 software (Chioccarelli et al., 2019) providing a conditioned spectrum of the site for different return periods of the seismic action. Based on the obtained mean conditioned spectra and relevant dispersions, procedures as described in the literature (Baker, 2011; Baker and Lee, 2018) have been applied to obtain set of records to be used for the non-linear analyses under increasing intensity levels characterized by return periods ranging from TR = 60 years to TR = 10000 years. The main demand parameters of both the isolation system and the super-structure have been recorded and capacity values corresponding to different ultimate and damage conditions have been defined. Finally, the demand hazard curves of the monitored demand parameters have been evaluated to quantify the exceedance probability of each limit state considered.
The structural system of the university research center was conceived around a design solution suitable for the complex morphology of the area and for the speed of execution and able to guarantee a high level of resilience and robustness to the construction. In particular, the foundations and the lower parts of the building have been designed to reduce the impact on the ground profile, which is characterized by a remarkable slope. The characteristics of the soil and the variability of the thickness of the deformable layer led to the adoption of deep foundations (Figure 1). The isolation system, consisting of high-damping elastomeric isolators and low-friction flat sliders, have been placed at the horizontal level above the sub-structure r.c. elements. The upper part of the building (super-structure) is made of steel elements and is developed by assuming a 7.2 m × 7.2 m modular system, for a total of 7 modules along each direction, and a 1.9 m long cantilever along the entire perimeter of building (Figure 2). The steel elements have been optimized in terms of dimensions and connection systems based on the single module, resulting in a significant saving on materials and a significant reduction in construction times.
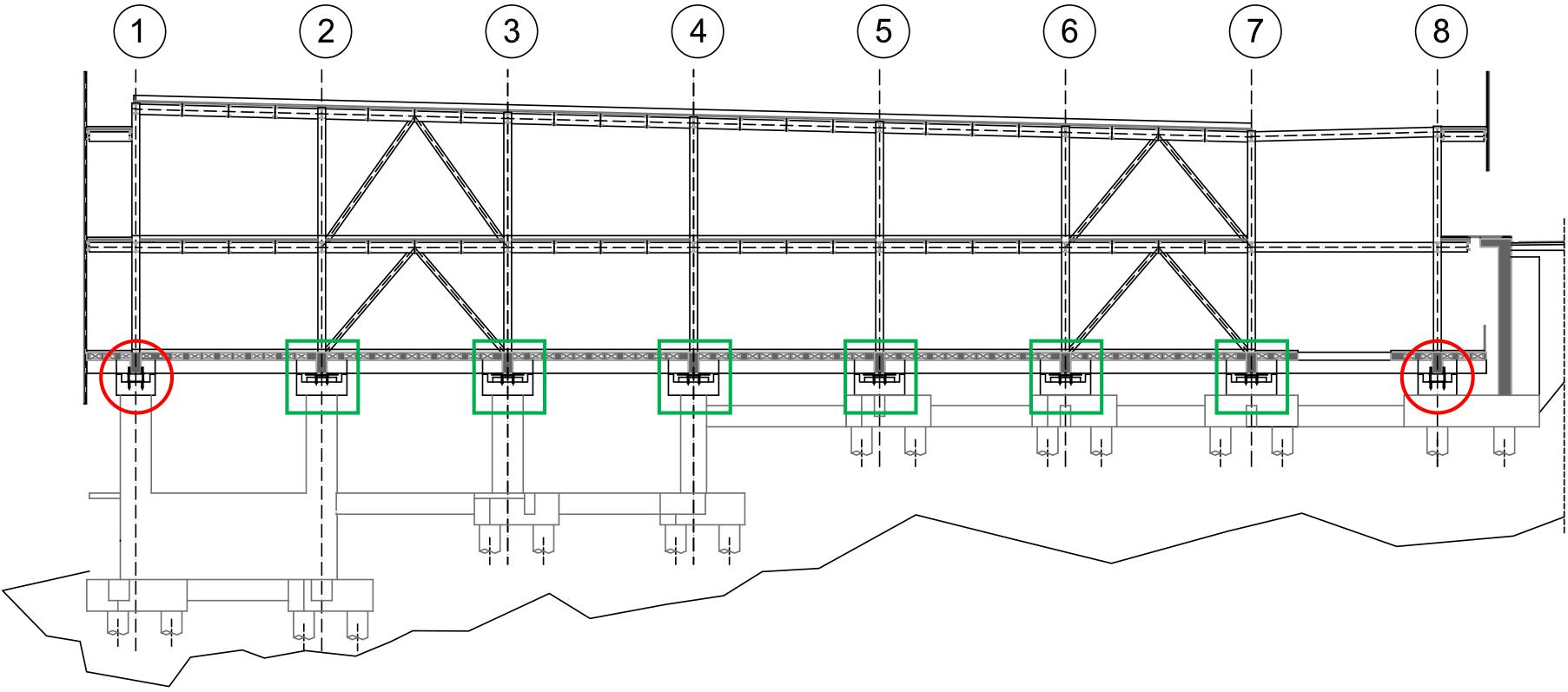
Figure 1. Longitudinal section of the building (red circles represent HDR bearings and green squares represent flat sliders).
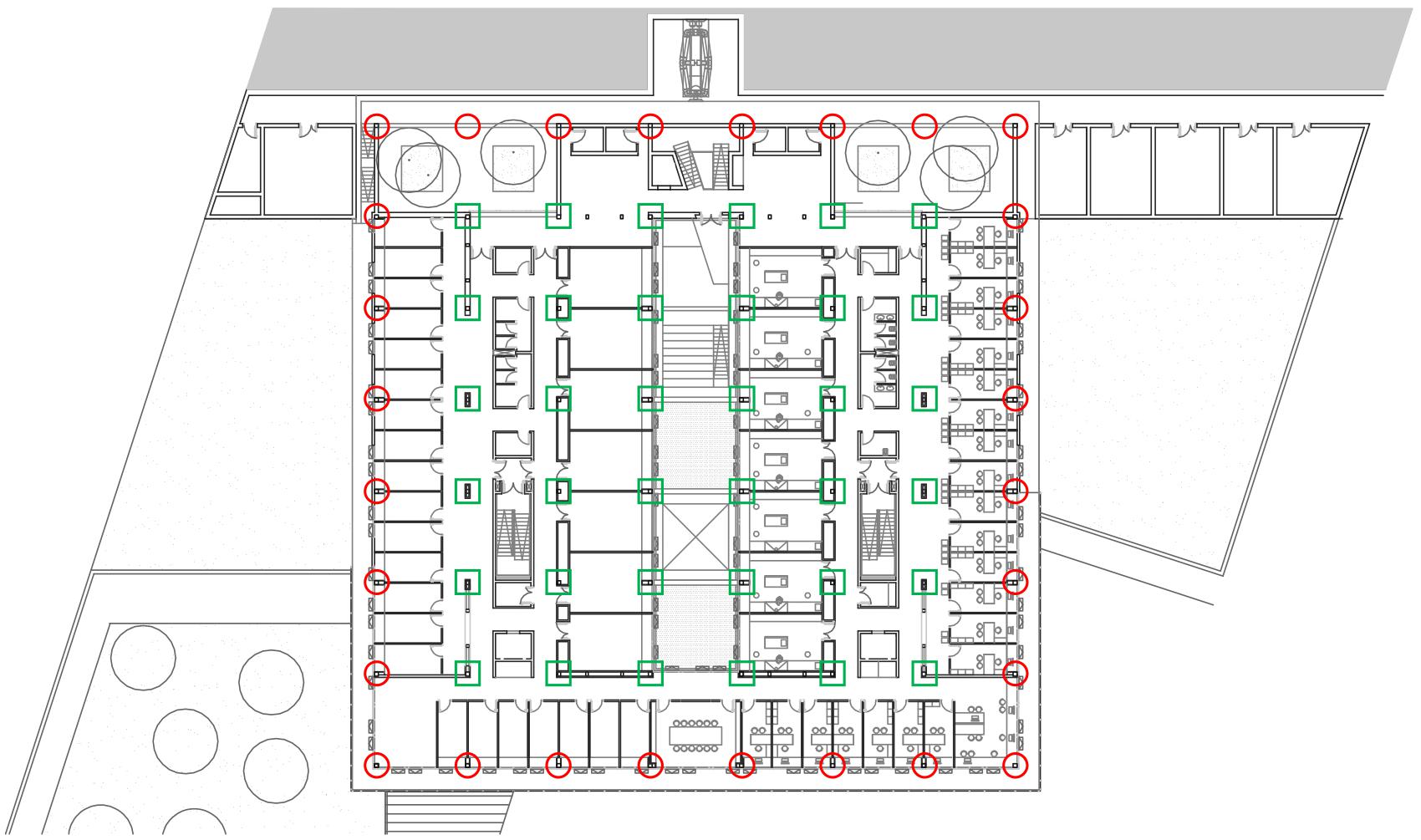
Figure 2. Plan view of the building (red circles represent HDRB bearings and green squares represent flat sliders).
The building is founded on a multi-level pile system, with piles of 0.8 m diameter and 14 m long. The foundation system on the head of the piles is composed of a set of plinths, of variable shapes and a height of 1.2 m, mutually connected by r.c. beams with a 0.4 m × 0.8 m cross section. All the elements are made of C25/30 concrete with B450C steel reinforcement bars. The columns of the sub-structures have a circular section of 1.2 m diameter or a 1 m × 1 m square section and they are only in the downstream part of the building (Figure 1). All the elements are made of C28/35 concrete with B450C steel reinforcement bars. At the head of each column, a capital allows for the easy maintenance and the replacement of seismic support systems (HDR bearings or sliders). These capitals are of two distinct types: (a) as a support for the elastomeric and (b) as support for the sliders to compensate for the different heights and to allow for vertical alignment of the top of all the devices (Figure 3). It is worth noting that the capitals are designed with specific reinforcements to withstand the forces acting on the super-structure during lifting for possible removing and replacement of the devices. Finally, they are all equipped with 4 safety supports (one on each corner) to ensure the transfer of vertical loads in cases of emergency (loss of support capacity of one or more devices).
The isolation system has been designed considering a target period of Tis = 3.5 s at the design intensity earthquake, able to guarantee a significant reduction of the actions transferred to the super-structure in the case of a seismic event. In particular, the solution adopted to guarantee this period involves the use of a hybrid isolation system with HDR bearings arranged on the perimeter in order to maximize torsional stiffness, and flat sliding supports in the central part to support higher vertical loads. HDR bearings commonly used in Italy have a damping ratio ranging from 10% to 15% (FIP, 2016), which is lower than HDR bearings used in other countries with higher seismicity areas, such as Japan (Bridgestone, 2017). In the design of the isolation system the lower limit of 10% at the design shear strain was assumed. However, according to EN15129 (2009), this rubber compound can still be classified as high damping, because the damping ratio is larger than the lower bound of 6% (at 100% of shear strain) fixed by the code. Moreover, a shear stiffness equal to 0.4 MPa was assumed at the design shear strain, typical of a soft rubber. For the flat sliding bearings, a friction coefficient of less than 1% was required. In a preliminary phase, the bearings were dimensioned by assuming a rigid super-structure and sub-structures to obtain a 1-DOF (degree of freedom system) and by neglecting the slider friction. Thus, the elastic response spectra have been used, reduced for all the periods T ≥ 0.8 Tis by the equivalent damping of the HDR bearings. Figure 4 shows the elastic displacement spectra and the pseudo-acceleration spectra for the considered site (Camerino, soil type B) at the different limit states: the Operational Limit State (OLS), the Damage Limit State (DLS), the Ultimate Limit State (ULS) and the Collapse Limit State (CLS), characterized by the return periods respectively equal to TR = 60 years, TR = 100 years, TR = 950 years, and TR = 1950 years, according to the national seismic code (NTC, 2018) for the use class IV. According to that code, the design was carried out by deriving the maximum displacement of the isolators from the displacement spectrum at the CLS corresponding to the isolation period of 3.5 s, which is about 0.27 m. An average design shear strain equal to 1.5 is assumed, ensuring a significant safety margin against possible shear failure, even in the presence of accidental torsional effects. In fact, by assuming an amplification of 1.2 (Dolce et al., 2013) for torsional effects, the maximum deformation is equal to 1.8, which is still lower than the maximum value allowed by the European standard on anti-seismic devices (EN15129, 2009) equal to 2.5. Based on the obtained displacement and the design shear strain of bearings the total height of rubber of the bearings is his = 0.27/1.5 = 0.18 m. The total area of rubber (Ais) able to guarantee the target isolation period can be deduced through the following relationship:
The total mass of the system is equal to M = 6173 kNms–2 therefore the total area obtained is equal to Ais = 9,087 m2. Based on the total rubber area obtained and on the devices available on the market, the following types of devices have been chosen: (i) elastomeric isolators with a diameter of 600 mm, total height of rubber 184 mm, with horizontal rigidity 0.62 kN/mm and maximum displacement 350 mm, (ii) sliding supports with a maximum displacement of 400 mm and friction coefficient lower than 1%. The final choice of devices led to a slightly higher isolation period equal to Tis = 3.60 s. It should be noted that the displacement capacity of both the devices is larger than the maximum displacement at the CLS accounting for torsional effects (270 ∗ 1.2 = 324 mm), especially for slider devices. As already highlighted in the introduction, this safety assumption guarantees the absence of anomalous behaviors due for example to the exit of the sliders for actions greater than those considered in the design. An adequate dimension has also been assumed for the seismic gaps placed in the upstream part of the building at the road level. In particular, high-performance floor gaps have been installed in the entrance areas, able to absorb the entire movement without damage and maintaining a horizontal surface even during the earthquake, while in the other areas standard gaps have been arranged, able to absorb the entire displacement but with damage to the rubber inserts beyond a certain threshold. In both cases, the displacement capacity assumed is equal to 350 mm. Similar precautions have been taken with regard to facilities, piping and installations, which must absorb the entire design displacement without damage or loss of functionality.
As already mentioned, the super-structure is articulated on two levels (for a total of three decks) and the structural system is made of steel. In particular, the structural system consists of beams and columns with pinned joints, that take on gravitational actions, while the resistance to horizontal actions is ensured by the diagonal tension-compression braces, arranged in a reverse V and placed in the two main directions of the building. HE300B type profile columns are used, for both elevations, whereas the main beams are made of HE400A type profiles and the secondary ones are made of IPE360 profiles. Braces have a hollow circular section with 193.6 mm diameter and 16 mm thickness. The first floor above the isolation plane is made of precast r.c. slabs (H = 5 + 20 + 5 cm) and beams of 40 × 80 cm sections arranged in both directions and designed by accounting for moments induced by P-Δ effects due to the large displacements of HDR bearings and sliders during the earthquake motion. The second and third floors are made of corrugated steel sheets and r.c. slabs (H = 75 + 55 mm), supported by secondary steel beams. For the external cantilever, present in all three levels, the structural systems of the respective floors are used. All the elements are made using S355 steel. Finally, twin staircases guarantee the vertical connection of the building. Since the staircases cross the isolation layer, a seismic gap has been placed below the first floor slab, and the arrival ramp has been cut to guarantee a relative displacement of 400 mm (Figure 5). There are other staircases in the building: a reinforced concrete staircase connecting the sub-structure to the first floor (also provided with a seismic cut to allow the relative displacement of the adjacent reinforced concrete beams and plinths in the arrival area) and two other steel staircases connecting the super-structure. There are also three elevators in the building, two of which reach the sub-structure. For these lifts, the part of the structure being under the isolation level is hanged on the floor just above the isolation system. In this way, the absence of any interference with the isolation system or the fixed parts of the sub-structure is ensured. At the underground level high-performance seismic floor gaps have been used to permit access to the lift and avoid impact between the hanged lift-case and the sub-structure during an earthquake.
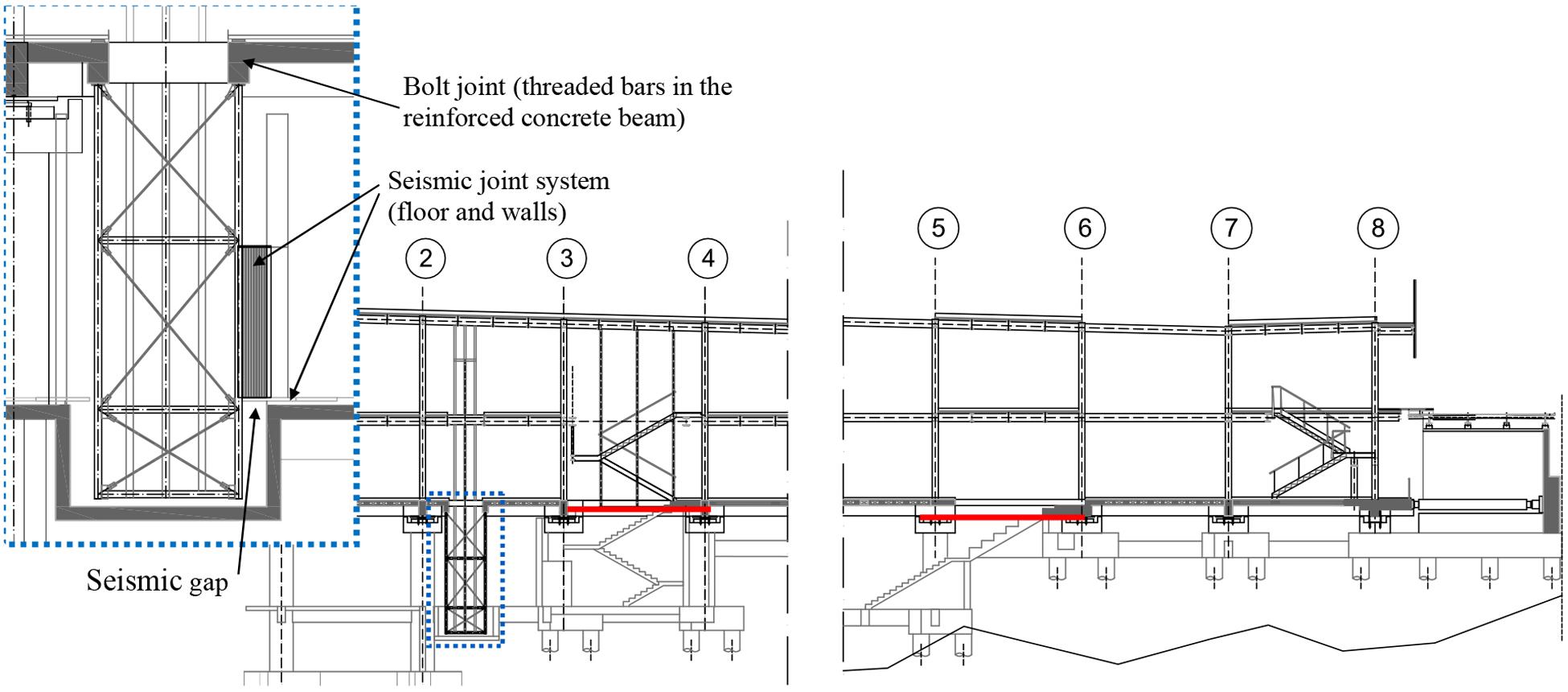
Figure 5. Sections of the building (the red line highlights the seismic cut of staircases whereas the blue dotted area highlights the steel frame of the hanged elevator).
For design purposes, seismic analyses of the building was carried out by modeling all the structural system components (the super-structure, the sub-structure and the isolation system) as linear elastic elements, having satisfied the conditions reported in NTC for the linear modeling of isolation systems (NTC, 2018). In particular, the isolation devices were modeled by means of linear elastic springs (HDR bearings) and sliding supports (sliders). For the bearings, the horizontal stiffness is assumed consistent with the level of displacement reached at each considered limit state. This was iteratively estimated based on the displacement spectra of the different limit states and the expressions available in the technical literature about rubber equivalent parameters (G and ξ) as a function of the obtained shear strain (FIP, 2016). It should be noted that the vertical deformability of the HDR bearings was also taken into account, despite the ratio between their vertical stiffness and horizontal stiffness being greater than 800, to verify the effect of the different vertical stiffness of sliders and bearings. Finally, all the decks are considered as rigid. The Sap 2000 software has been used for the analyses (Computer and Structures, 1995).
First, a modal analysis was carried out on the model, and the results, in terms of the three main vibration periods of the building, are presented in Table 1, together with mean values of the shear strains of bearings at the different limit states and the corresponding equivalent parameters. Thereafter, a spectral analysis was carried out by using elastic spectra reduced, for all periods T ≥ 0.8 Tis, of the equivalent damping of the isolation system, as illustrated in Figure 4. Only for the resistance verifications of the super-structure at the ULS, a behavior factor equal to q = 1.5 was assumed, in accordance with NTC (2018). However, as better explained later, the braces have been dimensioned based on a request for rigidity adequate for the isolation system, rather than for resistance. In this way, the structure is also insensitive to the second order effects and the effect of global imperfections in resistance verifications can be neglected. Finally, the over-strength of the braces provides a strategy to ensure adequate structural robustness, i.e., limited consequences in the case of exceptional horizontal actions causing an increase in the stiffness of the HDR bearings (due to their hardening behavior) or the closure of the gaps. Table 2 summarizes the base shear and displacement of the isolation system for the different limit states. For each limit state, the maximum and minimum axial load acting on the bearings, including the increase in axial load due to seismic actions, is also reported.
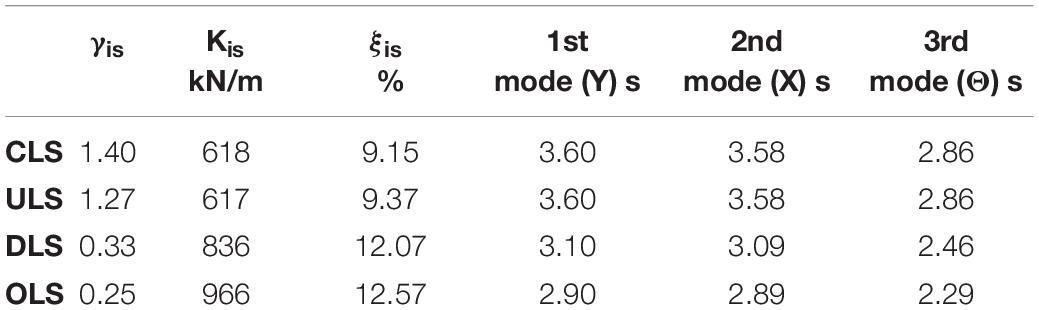
Table 1. Shear strain, stiffness and damping ratio of isolation bearings at different limit states and relevant vibration periods.

Table 2. Maximum base shear, maximum displacements of the isolation system and maximum compression forces on the isolation devices.
Firstly, it can be observed that the maximum displacements at the CLS are lower than the displacement capacity of the selected devices and no tensile forces occur on any devices (no cavitation for HDR bearings or uplift of sliders). Regarding maximum compression forces, the maximum values obtained in the seismic condition are about 1040 kN for the bearings and 1600 kN for the sliders. Under the static condition (the ultimate limit state without seismic action, not reported in this paper) the maximum axial loads are about 2100 kN for the bearings and 2400 kN for the sliders. The buckling capacity of the selected HDR bearings is sufficiently larger than the demand. In fact, given the primary shape factor S1 = D/4t (where D is the bearing diameter and t the thickness of a single rubber layer), the buckling load capacity at zero displacement can be computed through the following expression, as suggested by the European code for anti-seismic devices (EN15129, 2009):
where D′ is the effective diameter of the bearing (i.e., the diameter of steel plates without the rubber cover), Ar is the effective area of the device and Tq is the total rubber thickness called his in Eq. 1. Supposing that the selected HDR bearings are composed by 23 rubber layers of thickness 8 mm, the primary shape factor is S1 = 18.75 and the buckling load capacity is about 6640 kN. For the code, the maximum admissible compressive load at zero displacement is PCR/2 = 3320 kN, while the maximum admissible compressive load at the maximum admissible displacement equal to dmax,b = 0.7D′ is PCR/4 = 1660 kN. For the bearings selected dmax,b = 0.7D′ = 0.7⋅580 = 406 mm. Since the maximum axial load under static conditions is lower than the corresponding limit, and the fact that the maximum displacement and the maximum axial load obtained from the seismic analysis are both lower than the respective admissible values, the stability of the bearings is ensured. For the sliders, the diameter of the internal pad has been chosen, by assuming a maximum contact pressure on the elastomeric pad of about 60 MPa (EN 1337-5, 2005). By adopting a diameter of 270 mm and partial safety factor of γm = 1.3 (EN 1337-5, 2005) the maximum axial load is about Nb,Rd = 2640 kN, which is lower than the maximum axial load acting on the sliders. With regard to the super-structure and the sub-structures, all the elements have been checked for resistance (r.c. and steel elements) and stability (steel elements) at the ULS, moreover inter-storey drifts and absolute floor accelerations of the super-structure have been estimated for the different limit states (Table 3). It must be emphasized that the designed isolation system and the choice adopted for the non-structural elements (vertical closure panels) ensure the absence of any significant damage up to the CLS and therefore allow the construction to be operative immediately after the occurrence of a high intensity earthquake without any loss of functionality or downtime.
In order to accurately estimate the risk level of the base-isolate building, a probabilistic seismic risk analysis has been carried out, following a probabilistic framework already used for base-isolated structures as well as for other kinds of code-conforming structures (Iervolino et al., 2018; Ragni et al., 2018a). In particular, a hazard analysis of the site was first conducted, then non-linear dynamic analyses were carried out under increasing seismic intensities in order to assess the attainment of damage and ultimate conditions. Finally, linking information about the site hazard and the vulnerability of the building made it possible to estimate the seismic risk. Hereafter is reported a description of the procedure followed.
Probabilistic seismic hazard analysis (PSHA) is generally recognized as the rational method to quantify the seismic input in a probabilistic way, i.e., define the probability of exceedance (or the annual rate of exceedance) of a measure of the seismic intensity (IM). In order to make the implementation of this procedure less demanding for engineers dealing with practical applications, a practice-oriented software, namely REASSESS V2.0 (REgionAl, Single-SitE and Scenario-based Seismic hazard analysis) has recently been developed (Chioccarelli et al., 2019) and was used in the analyses of Camerino site. The software allows the user to define the input of the analysis in terms of: site coordinates, the Ground Motion Prediction Equation (GMPE) selected from an embedded database, the intensity measure (IM) of interest (according to the GMPE), the seismic sources (user-defined three-dimensional faults, seismic sources areal zones or sources selected from embedded databases), and structure of logic tree, if any. When these input elements are set, REASSESS is able to provide classical results of PSHA such as hazard curves, even in terms of advanced ground motion IM. Moreover, uniform hazard and conditional mean spectra (UHS and CMS), together with disaggregation distributions given the occurrence or the exceedance of the IM threshold, can be computed.
In this application the pseudo-acceleration spectral ordinate at the isolated period has been selected as the IM. With regard to the seismic zones and the GMPE, it is known that the seismic hazard study of Italy (Stucchi et al., 2011), at the basis of the current Italian building code, considers the seismic source model of the thirty-six areal zones defined by Meletti (Meletti et al., 2008) and the GMPE by Ambraseys (Ambraseys et al., 1996). In this study, the same source model has been considered, but a recently developed GMPE has been assumed (Lanzano et al., 2019). This GMPE is based on updated data including later events (i.e., 2012 Emilia, Northern Italy; 2016–2017 Central Italy), which allowed the magnitude range to be extended beyond 6.9 and the vibration period to be increased up to 10 s. Thus, it can also be used for long period structures, such as base-isolated structures. It should also be noted that this GMPE uses as IM the median of orientation independent amplitudes (RotD50) instead of the maximum component in the two directions, as in Ambraseys (Ambraseys et al., 1996). Figure 6A shows the computed hazard curves for different spectral ordinates and for the site of interest with soil classes B (vs = 400 m/s). The Uniform Hazard Spectrum (UHS) for different return periods is indicated in Figure 6B. Note that Figure 6B also illustrates the UHS given by the Italian seismic code (NTC, 2018) for the same site and for the CLS (TR = 1950 years). Although the source model considered in this paper for the hazard assessment lies at the basis of the hazard map used by the code, the latter is based on a different GMPE. Furthermore, a logic tree was considered for the hazard map definition, while only one branch has been considered in this study. Therefore, the UHS obtained for TR = 1950 years is different from the code UHS, in particular it is larger for short periods but lower for long periods typical of base-isolated structures. However, it should be noted that this comparison is only qualitative, because the code spectrum is referred to a different IM (maximum component instead of RotD50).
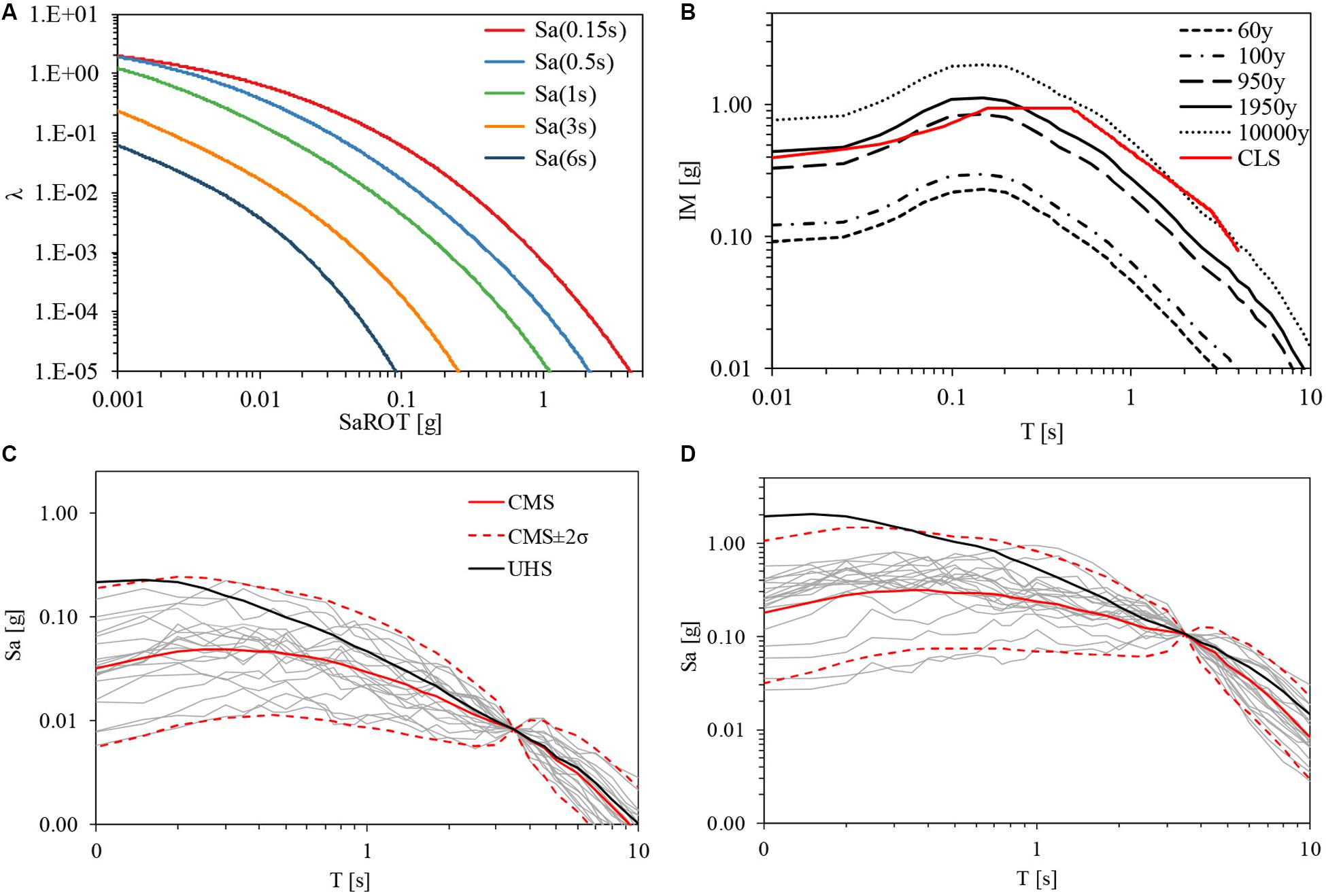
Figure 6. Hazard Curves for the Camerino site with vs = 400 m/s (A), UHS at different hazard periods (B), CMS and spectra of the selected set of records for TR = 60 years (C), and TR = 10000 years (D).
In this study, for the non-linear analyses reported in the next section the return periods of the design limit states (TR = 60 years for the OLS, TR = 100 years for the DLS, TR = 950 years for the ULS, TR = 1950 years for the CLS) have been considered together with a larger return period of TR = 10000 years. For each return period, a hazard consistent seismic input has been chosen for non-linear dynamic analysis. Practically, this means that records were selected to be consistent with the hazard-based spectral shape and variability obtained for each return period, by using the methods available in the technical literature (Baker, 2011; Baker and Lee, 2018). In particular, for each intensity level a set of 20 records was selected by extracting them from the ESM database (Luzi et al., 2016). Figures 6C,D illustrate the pseudo-acceleration spectra of the selected record for returns periods of TR = 60 years and TR = 10000 years. The CMS is also shown together with an interval corresponding to twice the standard deviation (σ) in which almost all the records are included. A specific study with only pulse-like motions is not carried out, according to EC8 indications (EN 1998-1, 2005), since a fault closer than 15 Km and with a Magnitude larger than 6.5 is not known for the Camerino site.
For the non-linear dynamic analyses a non-linear numerical model has been developed, starting from the linear model used in the design phase. In particular, linear springs representing the HDR bearings have been replaced by non-linear elements adopting the HDR isolator (Masaki et al., 2017) available in the Sap 2000 software (Computer and Structures, 1995). This model is bidirectional and accounts for non-linear phenomena, such as the strain-dependent behavior of the HDR bearings, but neglects other aspects, such as the strain hardening at large shear strains (larger than 250%) or the effect of the vertical load on the horizontal response of the bearings (Ishii and Kikuchi, 2018). This may be important for large axial loads close to the buckling capacity of the bearing in the deformed configuration (Kelly, 1997). The load history dependence characterizing some HDR bearings has also been neglected. This last aspect concerns bearings made of natural rubber with a large amount of filler, causing progressive damage to the rubber microstructure as the strain history progresses. Although there are numerical models accounting for this phenomenon in scientific literature (Grant et al., 2004; Tubaldi et al., 2017; Ragni et al., 2018b), it has been neglected in this study and the numerical model adopted for the bearings has been calibrated based on third cycle data available in the technical literature (FIP, 2016). More in details, model parameters have been calibrated to obtain target stiffness and damping data at each shear deformation. The cyclic behavior obtained is reported in Figure 7A and the equivalent linear parameters are illustrated in Figures 7B,C. The hardening at large shear strains as well as the effect of the vertical load on the horizontal response of the bearings were also neglected in these analyzes, due to the limited maximum shear strain and maximum axial load experienced by the bearings, even in very rare events. With reference to the sliding supports, these have been modeled as friction elements with constant friction coefficient equal to 0.5% (typical of dimpled lubricated PTFE sheet on austenitic steel, EN 1337-5, 2005), neglecting its dependency on sliding velocity, contact pressure or heating during repeated cycles. This choice is supported by the expected low effect on the global behavior of the hybrid system of the variation of the friction coefficient. More sophisticated models, based on available numerical and experimental studies accounting for these three effects (Lomiento et al., 2013; De Domenico et al., 2018, 2019; Furinghetti et al., 2019), should be used to analyze the response of base-isolated buildings equipped with high or medium friction CSSs, where the primary function is to support vertical loads and to provide energy dissipation. The elastic behavior of the super-structure has been maintained by checking that the elastic limit of the diagonal braces has not been exceeded for each time history. Finally, seismic gaps have not been included in the model, but for each time history it has been checked whether displacements were smaller or larger than the gap amplitude.

Figure 7. Cyclic behavior of the HDR model of the Sap 2000 software (A) and trends pf equivalent stiffness (B) and equvalent damping (C).
Figures 8, 9 show the results of the non-linear analyses carried out for the different intensity levels considered. In particular, Figure 8 shows the seismic demand on the isolation system, in terms of the maximum displacement attained by the HDR bearings (Figure 8A) and the sliding supports (Figure 8B). First, it can be observed than mean values are lower than those expected from the design, for all the design limit states (OLS with TR = 60 years, DLS with TR = 100 years, ULS with TR = 950 years, and CLS with TR = 1950 years). This is due to the different hazards assumed in the design and seismic risk assessment phases, but also to the different structural models and types of analysis used in the two phases. An important role is played by the slider friction (neglected in the design but considered in seismic risk assessment) which reduces the displacement demand of the isolation system while slightly increasing accelerations transferred to the super-structure. The second remark is about the dispersion of the monitored repose parameters due to the record-to-record variability, which is particularly evident at IM5. The reason of this variability can be explained by Figure 10, where displacement spectra of the records selected at IM5 are illustrated in terms of RotD100 (SdRotD100), i.e., the maximum spectral value over all the rotation angles of the bidirectional signal. In order to simulate displacements sustained by the isolated building, spectra are computed by assuming a damping ratio equal to ξ = 10%. It can be observed that even though records are scaled to obtain the same intensity measure in terms of RotD50 at the isolation period (as shown in Figure 7), a significant record-to-record variability is obtained at the same period for spectral displacement in terms of RotD100, due the different record directivity. The three earthquakes leading to the highest displacements of the isolation system are the same earthquakes with the highest values around the isolation period.
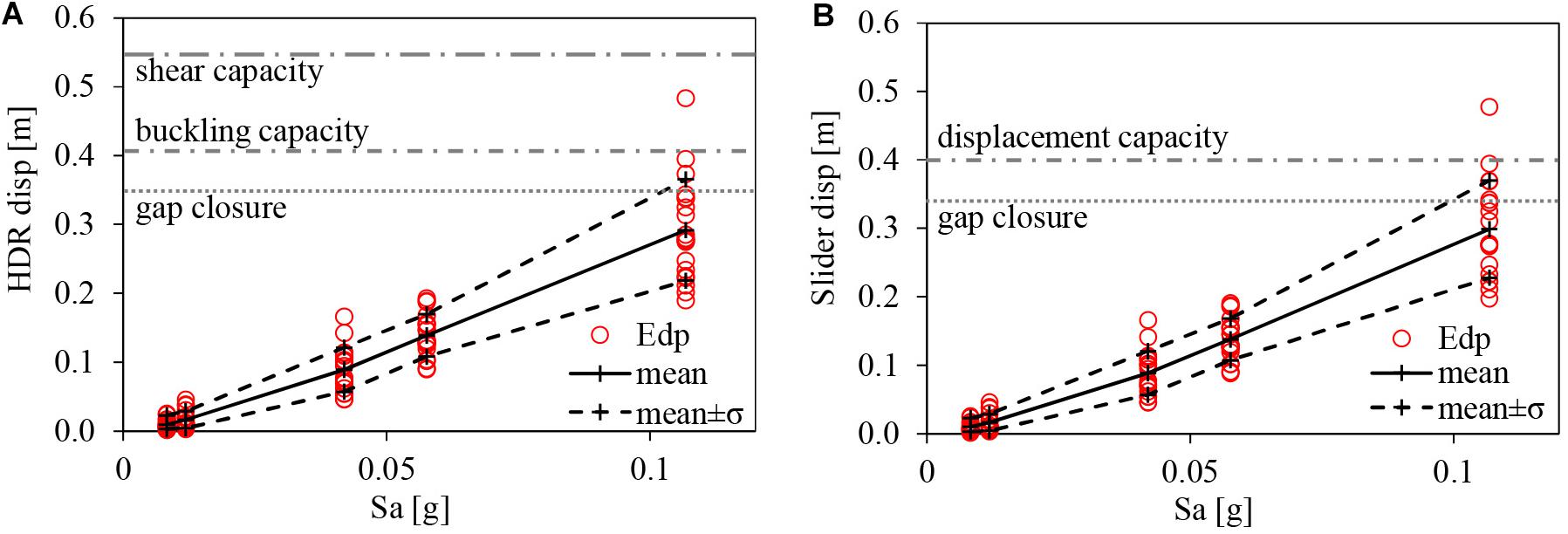
Figure 8. Maximum displacement of HDR bearings (A) and sliders (B) and the corresponding capacity limits.
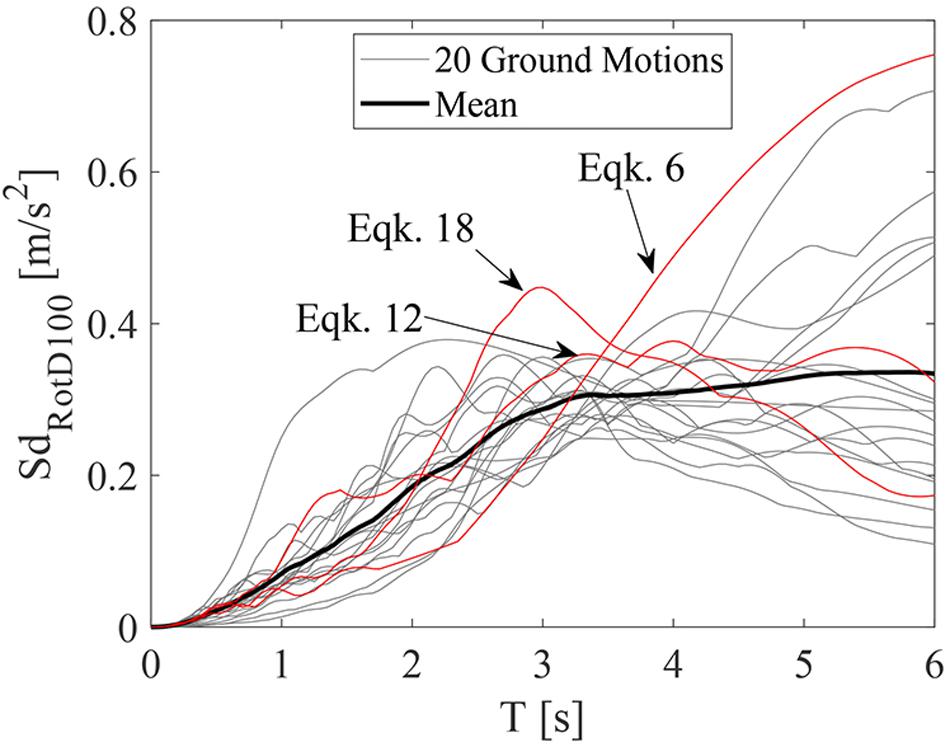
Figure 10. Displacement spectra in terms of RotD100 of the selected set of records for TR = 10000 years.
The capacity limits corresponding to different limit states are also highlighted in Figures 8, 9. In particular, for HDR bearings (Figure 8A) the gap amplitude equal to 350 mm is reported as well as the maximum admissible displacement for the buckling stability equal to dmax,b = 0.7D′ = 0.7⋅580 = 406 mm. The maximum displacement corresponding to the shear failure (dmax,s) of the bearings is also reported, assuming a shear capacity equal to 300% (dmax,s = 3⋅his = 546 mm). This limit corresponds to the maximum value at which an HDR bearing may be tested to verify its horizontal displacement capacity, according to the code on anti-seismic devices (EN15129, 2009). In fact, for the code the maximum admissible shear strain due to the horizontal displacement is 2.5 and the partial factor to be used in the test is 1.15 for elastomeric isolators. Thus, the maximum tested strain would be 2.5 ⋅ 1.15 = 2.9. Experimental and numerical evidence (Montuori et al., 2016; Brandonisio et al., 2017; Ragni et al., 2019) shows larger shear capacity limits, but these depend heavily on the rubber compound, on the isolator shape as well as on the manufacturer, thus a conservatory value of 300% has been assumed in this study. Notwithstanding, as observed in Figure 8A, the shear capacity limit assumed is never attained, not even for the largest return period. Differently, for the largest IM with TR = 10000 years the gap amplitude is exceeded in three time histories whereas the maximum admissible displacement for the buckling stability only once. However, actually the impact is reached only once (for earthquake n°6), because maximum displacements are not along the direction orthogonal to the retaining walls and for the other two time-histories the displacement components in these directions are both lower than the gap amplitude. Since the maximum axial load is lower than PCR/4 = 1660 kN for all the time histories carried out at that IM, only for one record the buckling requirement was not satisfied. Regarding the sliders (Figure 8B), also in this case the maximum axial loads obtained are always lower than the vertical capacity assumed for the sliders (Nb,Rd = 2640 kN) and their displacement capacity is only reached once, for the same time history leading to the maximum admissible displacement for the buckling stability of HDR bearings. However, it should be noted that attainment of the gap closure is not a collapse condition, it only makes necessary a more accurate model of the base-isolation system, where contact elements for the gaps are included to investigate the effects of their closure on the super-structure. With this model, displacement larger than the gap amplitude will be still possible in the direction opposed to the gap (placed only at the upstream side of the building), thus advanced models of bearings (accounting for their post-buckling behavior) and sliders (accounting for their over-stroke behavior) should also be included in the more accurate model. In fact, according to the most recent research outcomes, HDR bearings are able to show a post-buckling behavior up to a maximum displacement equal to the effective diameter of the bearing (Montuori et al., 2016) and sliders can reach an ultimate displacement almost equal to the capacity of the slider increased by half of the internal pad diameter (Ragni et al., 2018a).
With reference to the super-structure, maximum inter-storey drifts are illustrated in Figure 9A, while absolute floor accelerations are shown in Figure 9B. It is evident that, due to the high degree of stiffness of the super-structure, inter-storey drifts remain limited up to the largest IM, whereas absolute accelerations become significant for the largest return periods. In this case, the mean values obtained are lower than the design ones for the inter-storey drifts but are larger for the floor absolute accelerations. Differences can be ascribed to the same reasons explained for the isolation system displacements. According to technical literature, damage limits for displacement-sensitive elements may be assumed equal to 0.33% of the story height, equal to 0.0033⋅4300 = 14.2 mm (Okazaki et al., 2007; Scozzese et al., 2017, 2018). For the acceleration-sensitive components a limit of 0.2 and 0.4 g is assumed for slight and moderate damage, respectively (Hazus-MH 2.1, 2001). It is evident from the results that the displacement limit is never reached. Similarly, the acceleration limit corresponding to moderate damage is exceeded only in one case at the largest IM, whereas the light damage level is also reached at lower IM, but excluding the first two intensity levels. Displacements and flexural moments of the sub-structure columns have not been reported, because they are very small and far from their resistance limit. The obtained results confirm that only in one case at the largest IM (record n.6) the moderate damage limit is exceeded. However, in this case maximum displacements and accelerations would be even larger than registered values, because of the impact with the retaining wall. Also the axial force acting on the diagonal steel braces (about 800 kN for record n.6) could be larger and could exceed the buckling capacity of the brace equal to Nb,Rd = 1630 kN. However, to estimate exact values of these response parameters a gap element should be included in the model. Different contact models are available in the technical literature (Pant and Wijeyewickrema, 2014), however stiffness and damping capacity of the model must properly selected in order to obtain reliable results.
Figures 11, 12 illustrate the hazard curves relevant to the demand parameter described above and expressing the mean rate of annual exceedance (λ) for each level of the demand parameter considered. These curves have been computed by combining the results obtained in the seismic hazard assessment and in the non-linear dynamic analyses using the total probability theorem. Since these results are available only as discrete values, this calculation is not solvable in closed form. The procedure followed in this study to compute these hazard curves starting from discrete values is that one suggested by Porter (2019). Observing the demand hazard curves obtained for the maximum displacement of the isolation system it is evident that the mean annual rate of exceedance of the gap closure is very low. The obtained value is about 2⋅10–5, which is significantly lower than 2⋅10–4 suggested by the American seismic code (ASCE 7 16) and the draft annex of the new Eurocode 8 (Fajfar, 2018), as maximum value for the structural safety. Furthermore, the mean annual frequency of exceedance of the ultimate conditions corresponding to the buckling capacity of HDR bearings and the displacement capacity of the sliders is lower than 10–5. This confirming the high level of safety and robustness of the building. Regarding the super-structure performance, the hazard curves obtained for the inter-storey drift and the floor acceleration show that only the light damage state of acceleration-sensitive components has an exceedance probability larger than 10–5, confirming the high level of resilience of the building, i.e., a very low probability of a damage level causing the downtime of the building.
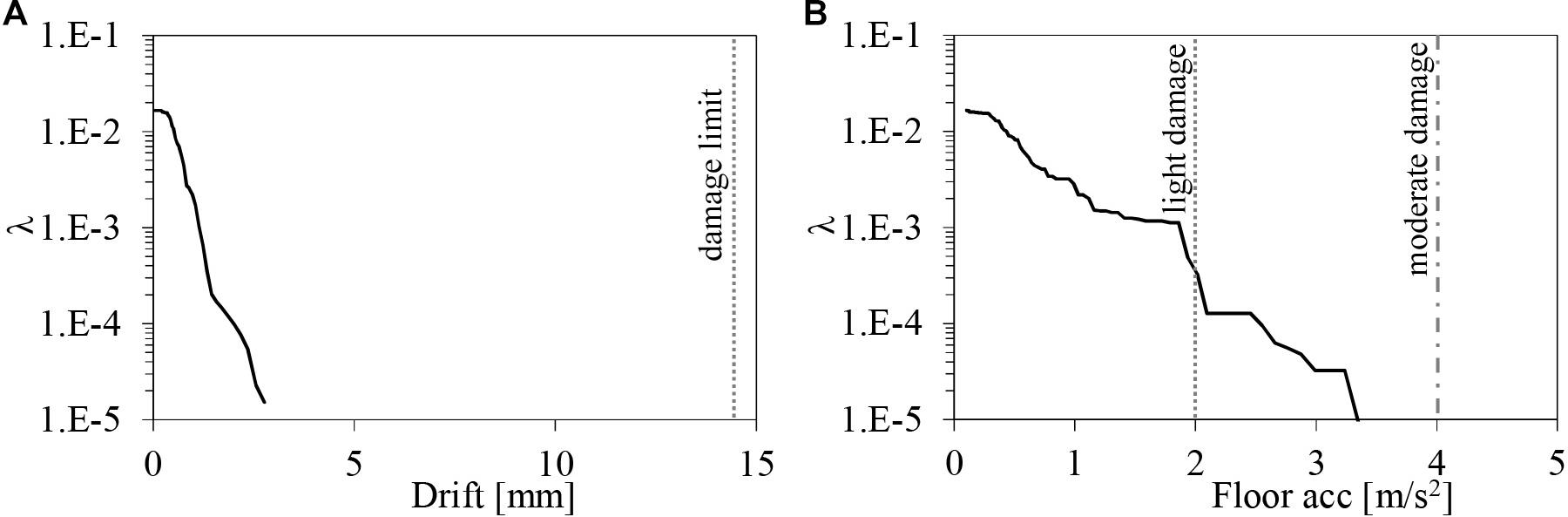
Figure 12. Hazard curve of the maximum inter-storey drift (A) and the maximum floor absolute acceleration (B).
It should be noted that the procedure followed to build the hazard curves accounts for the variability of the seismic input, i.e., the record-to-record variability (Scozzese et al., 2020). In this study this variability is due to the selection of the natural records according to the conditional spectrum of the site; alternatively it could be simulated by using a stochastic model of the input, as already done for different structural systems (Chen et al., 2007; Peng et al., 2013; Altieri et al., 2018). Furthermore, the variability of the properties of the isolation devices could also be considered. A more complete probabilistic framework accounting for both the variability sources should be applied in this case, as already carried out for structural systems with seismic isolation or dissipative devices (Dall’Asta et al., 2017; Franchin et al., 2018; Scozzese et al., 2019).
In this paper the new research center of the Camerino University has been described and analyzed. The building was designed to achieve speed of execution as well as a high level of safety, especially with regard to seismic activity. The structural solution was to create an isolated system with a steel braced super-structure with pinned joints and r.c. sub-structures able to adapt to the complex morphology of the area. In particular, a hybrid isolation system was adopted, comprising High Damping Rubber (HDR) bearings and low-friction sliders, able to provide a high period of isolation and thus to drastically reduce actions in the super-structure for both low intensity earthquakes and very severe seismic events. The first part of the paper focuses on the building description and the linear analyses carried out during the design phase, while in the second part the paper addresses specific risk analyses aimed at demonstrating the very low exceedance probability of damage and ultimate limit conditions, as defined for the structural system. To this purpose a site-specific hazard study was first carried out, then non-linear analyses were performed using a hazard-consistent set of records selected from the European strong motion database. The main demand parameters of both the isolation system and the super-structure were recorded, then capacity values corresponding to ultimate and damage limit conditions were assumed. Then, as final result, the demand hazard curves have been computed for the isolation system and for the super-structure. The obtained curves show that the mean annual rate of exceedance of the gap closure is significantly lower than the code prescription and the mean annual rates of exceedance of the limit states corresponding to the buckling capacity of HDR bearings and the displacement capacity of the sliders are even lower. Regarding the super-structure, the hazard curves obtained for the inter-storey drift and the floor acceleration show that only the light damage state of acceleration-sensitive components has an exceedance probability larger than 10–5. These results confirm the high level of safety and robustness of the building as well as the high level of resilience, i.e., a very low probability of disproportioned consequences due to seismic action larger than the design ones as well as a low probability of a damage level causing the downtime of the building. Finally, it is worth noting that the seismic risk assessment carried out in this paper is based on conservative hypotheses. Further analysis should be carried out with a more advanced model, including contact elements for seismic gaps as well as advanced non-linear models able to describe the post-buckling behavior of the HDR bearings and the extra-stroke behavior of the sliders, to more accurately estimate the real collapse probability of the building. Furthermore, a more complete probabilistic framework should be applied, also including a local site hazard analysis as well as the uncertainty affecting the structural system. Finally, floor response spectra should be also evaluated in order to assess the damage risk of possible flexible acceleration-sensitive components inside the building.
The datasets generated for this study are available on request to the corresponding author.
AD and GL designed base-isolated building with the contribution of FM and LG. LG, FM, and LR performed the numerical analyses and processed the analytical results. All authors have contributed to the manuscript revision, read, and approved the submitted version.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Altieri, D., Tubaldi, E., De Angelis, M., Patelli, E., and Dall’Asta, A. (2018). Reliability-based optimal design of nonlinear viscous dampers for the seismic protection of structural systems. Bull. Earthq. Eng. 16, 963–982. doi: 10.1007/s10518-017-0233-4
Ambraseys, N. N., Simpson, K. A., and Bommer, J. J. (1996). Prediction of horizontal response spectra in Europe. Earthq. Eng. Struct. Dyn. 25, 371–400. doi: 10.1002/(SICI)1096-9845(199604)25:4<371::AID-EQE550>3.0.CO;2-A
Baker, J. W. (2011). Conditional mean spectrum: tool for ground-motion selection. J. Struct. Eng. 137, 322–331. doi: 10.1061/(ASCE)ST.1943-541X.0000215
Baker, J. W., and Lee, C. (2018). An improved algorithm for selecting ground motions to match a conditional spectrum. J. Earthq. Eng. 22, 708–723. doi: 10.1080/13632469.2016.1264334
Brandonisio, G., Ponzo, F., Mele, E., and De Luca, A. (2017). “Prove sperimentali di isolatori elastomerici: influenza del carico verticale V e del fattore di forma secondario S2,” in Proceedings of the XIV Convegno ANIDIS “L’ingegneria Sismica in Italia”. 17–21 Settembre, Pistoia.
Bridgestone (2017). Seismic Isolation Product Line-up. Available online at: www.bridgestone.com (October, 2019).
Chen, J., Liu, W., Peng, Y., and Li, J. (2007). Stochastic seismic response and reliability analysis of base-isolated structures. J. Earthq. Eng. 11, 903–924. doi: 10.1080/13632460701242757
Chioccarelli, E., Cito, P., Iervolino, I., and Giorgio, M. (2019). REASSESS V2.0: software for single- and multi-site probabilistic seismic hazard analysis. Bull. Earthq. Eng. 17, 1769–1793. doi: 10.1007/s10518-018-00531-x
Computer and Structures (1995). SAP2000, Structural Analysis Program. Berkeley, CA: University Ave., Berkeley.
Dall’Asta, A., Scozzese, F., Ragni, L., and Tubaldi, E. (2017). Effect of the damper property variability on the seismic reliability of linear systems equipped with viscous dampers. Bull. Earthq. Eng. 15, 5025–5053. doi: 10.1007/s10518-017-0169-8
De Domenico, D., Ricciardi, G., and Benzoni, G. (2018). Analytical and finite element investigation on the thermo-mechanical coupled response of friction isolators under bidirectional excitation. Soil Dyn. Earthq. Eng. 106, 131–147. doi: 10.1016/j.soildyn.2017.12.019
De Domenico, D., Ricciardi, G., Infanti, S., and Benzoni, G. (2019). Frictional heating in double curved surface sliders and its effects on the hysteretic behavior: an experimental study. Front. Built Environ. 5:74. doi: 10.3389/fbuil.2019.00074
Dolce, M., Arleo, G., Di Cesare, A., and Ponzo, F. C. (2013). Progetto di Edifici con Isolamento Sismico (Italiano). Pavia: IUSS Press.
EN 1337-5 (2005). “EN 1337-5: Structural Bearings – Part 5: Pot Bearings”. Brussels: European Committee for Standardization.
EN 1998-1 (2005). Eurocode 8: Design of Structures for Earthquake Resistance – Part 1: General Rules, Seismic Actions and Rules for Buildings. Brussels: European Committee for Standardization.
EN15129 (2009). “UNI EN 15129: “Antiseismic Devices”. Brussels: European Committee for Standardization.
Fajfar, P. (2018). Analysis in seismic provisions for buildings: past, present and future. Bull. Earthq. Eng. 16, 2567–2608. doi: 10.1007/s10518-017-0290-8
FIP (2016). S02-Isolatori Elastomerici Serie SI (italian). Available online at: www.fipindustriale.it (October, 2019).
Franchin, P., Ragni, L., Rota, M., and Zona, A. (2018). Modelling uncertainties of Italian code-conforming structures for the purpose of seismic response analysis. J. Earthq. Eng. 22, 1964–1989. doi: 10.1080/13632469.2018.1527262
Furinghetti, M., Pavese, A., Quaglini, V., and Dubini, P. (2019). Experimental investigation of the cyclic response of double curved surface sliders subjected to radial and bidirectional sliding motions. Soil Dyn. Earthq. Eng. 117, 190–202. doi: 10.1016/j.soildyn.2018.11.020
Grant, D. N., Fenves, G. L., and Whittaker, A. (2004). Bidirectional modelling of high-damping rubber bearings. J. Earthq. Eng. 8, 161–185. doi: 10.1080/13632460409350524
Iervolino, I., Spillatura, A., and Bazzurro, P. (2018). Seimic structural reliability of code-conforming Italian buildings. J. Earthq. Eng. 22(Suppl. 2), 5–27. doi: 10.1080/13632469.2018.1540372
Ishii, K., and Kikuchi, M. (2018). Improved numerical analysis for ultimate behavior of elastomeric seismic isolation bearings. Earthq. Eng. Struct. Dyn. 48, 65–77. doi: 10.1002/eqe.3123
Kelly, J. M. (1997). Earthquake-Resistant Design with Rubber. London: Springer. doi: 10.1007/978-1-4471-0971-6
Lanzano, G., Luzi, L., Pacor, F., Felicetta, C., Puglia, R., Sgobba, S., et al. (2019). A revised ground−motion prediction model for shallow crustal earthquakes in Italy. Bull. Seismol. Soc. Am. 109, 525–540. doi: 10.1785/0120180210
Lomiento, G., Bonessio, N., and Benzoni, G. (2013). Friction model for sliding bearings under seismic excitation. J. Earthq. Eng. 17, 1162–1191. doi: 10.1080/13632469.2013.814611
Luzi, L., Puglia, R., Russo, E., and Orfeus WG5. (2016). Engineering Strong Motion Database, Version 1.0. Rome: Istituto Nazionale di Geofisica e Vulcanologia, Observatories & Research Facilities for European Seismology. doi: 10.13127/ESM
Masaki, N., Mori, T., Murota, N., and Kasai, K. (2017). “Validation of hysteresis model of deformation-history integral type for high damping rubber bearings,” in Proceedings of the 16th World Conference on Earthquake, Santiago Chile, January 9th to 13th 2017, Santiago.
Meletti, C., Galadini, F., Valensise, G., Stucchi, M., Basili, R., Barba, S., et al. (2008). A seismic source zone model for the seismic hazard assessment of the Italian territory. Tectonophysics 450, 85–108. doi: 10.1016/j.tecto.2008.01.003
Montuori, G. M., Mele, E., Marrazzo, G., Brandonisio, G., and De Luca, A. (2016). Stability issues and pressure–shear interaction in elastomeric bearings: the primary role of the secondary shape factor. Bull. Earthq. Eng. 14, 569–597. doi: 10.1007/s10518-015-9819-x
NTC (2018). “Norme Tecniche per le Costruzioni”, Decreto Ministeriale del 17 Gennaio 2 (ItalianBuilding Code, 2008). Lugano-Paradiso: NTC.
Okazaki, T., Nakashima, M., Suita, K., and Matusmiya, T. (2007). Interaction between cladding and structural frame observed in a full-scale steel building test. Earthq. Eng. Struct. Dyn. 36, 35–53. doi: 10.1002/eqe.618
Pant, D. R., and Wijeyewickrema, A. C. (2014). Performance of base-isolated reinforced concrete buildings under bidirectional seismic excitation considering pounding with retaining walls including friction effects. Earthq. Eng. Struct. Dyn. 43, 1521–1541. doi: 10.1002/eqe.2409
Peng, Y., Ghanem, R., and Li, J. (2013). Generalized optimal control policy for stochastic optimal control of structures. Struct. Control Health Monitor. 20, 187–209. doi: 10.1002/stc.483
Porter, K. (2019). A Beginner’s Guide to Fragility, Vulnerability, and Risk. Boulder, CO: University of Colorado Boulder, 119.
Ragni, L., Cardone, D., Conte, N., Dall’Asta, A., Di Cesare, A., Flora, A., et al. (2018a). Modelling and seismic response analysis of Italian code-conforming base-isolated buildings. J. Earthq. Eng. 22(Suppl. 2), 198–230. doi: 10.1080/13632469.2018.1527263
Ragni, L., Micozzi, F., Brandonisio, G., Dall’Asta, A., De Luca, A., Di Cesare, A., et al. (2019). “Comportamento dei dispositivi HDRB sotto grandi spostamenti ed elevati carchi assiali,” in Proceedings of the XV Convegno ANIDIS “L’ingegneria Sismica in Italia”. 15–19 Settembre, Ascoli Piceno.
Ragni, L., Tubaldi, E., Dall’Asta, A., Ahmadi, H., and Muhr, A. (2018b). Biaxial shear behaviour of HDNR with Mullins effect and deformation-induced anisotropy. Eng. Struct. 154, 78–92. doi: 10.1016/j.engstruct.2017.10.060
Scozzese, F., Dall’Asta, A., and Tubaldi, E. (2019). Seismic risk sensitivity of structures equipped with anti-seismic devices with uncertain properties. Struct. Safety 77, 30–47. doi: 10.1016/j.strusafe.2018.10.003
Scozzese, F., Terracciano, G., Zona, A., Della Corte, G., Dall’Asta, A., and Landolfo, R. (2017). “Rintc project: nonlinear dynamic analyses of Italian code-conforming steel single-storey buildings for collapse risk assessment,” in Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2017) – Rhodes Island, Greece, 15–17 June 2017, Rhodes. doi: 10.7712/120117.5513.17301
Scozzese, F., Terracciano, G., Zona, A., Della Corte, G., Dall’Asta, A., and Landolfo, R. (2018). Analysis of seismic non-structural damage in single-storey industrial steel buildings. Soil Dyn. Earthq. Eng. 114, 505–519. doi: 10.1016/j.soildyn.2018.07.047
Scozzese, F., Tubaldi, E., and Dall’Asta, A. (2020). Assessment of the effectiveness of Multiple-Stripe Analysis by using a stochastic earthquake input model. Bull Earthquake Eng. doi: 10.1007/s10518-020-00815-1
Stucchi, M., Meletti, C., Montaldo, V., Crowley, H., Calvi, G. M., and Boschi, E. (2011). Seismic hazard assessment (2003–2009) for the Italian building code. Bull. Seismol. Soc. Am. 101, 1885–1911. doi: 10.1785/0120100130
Tubaldi, E., Ragni, L., Dall’Asta, A., Ahmadi, H., and Muhr, A. (2017). Stress-softening behaviour of HDNR bearings: modelling and influence on the seismic response of isolated structures. Earthq. Eng. Struct. Dyn. 46, 2033–2054. doi: 10.1002/eqe.2897
Keywords: base isolation, high damping rubber bearings, hybrid isolation system, seismic risk analysis, hazard demand curves
Citation: Dall’Asta A, Leoni G, Micozzi F, Gioiella L and Ragni L (2020) A Resilience and Robustness Oriented Design of Base-Isolated Structures: The New Camerino University Research Center. Front. Built Environ. 6:50. doi: 10.3389/fbuil.2020.00050
Received: 13 December 2019; Accepted: 30 March 2020;
Published: 28 April 2020.
Edited by:
Solomon Tesfamariam, The University of British Columbia, CanadaCopyright © 2020 Dall’Asta, Leoni, Micozzi, Gioiella and Ragni. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dall’Asta Andrea, YW5kcmVhLmRhbGxhc3RhQHVuaWNhbS5pdA==; Fabio Micozzi, ZmFiaW8ubWljb3p6aUB1bmljYW0uaXQ=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.