An Efficient Stochastic Linearisation Procedure for the Seismic Optimal Design of Passive Control Devices

The seismic response of structures is often enhanced by introducing passive control devices that can operate through the dissipation of the input energy or by modifying the dynamic characteristics of the main structure. The inherent non-linearities in the constitutive laws of some of them lead to computation difficulties and have limited the large-scale use and design of these devices. In this study, a procedure for the optimal design of multi passive control devices is proposed. The general case of linear Multi-Degree-Of-Freedom (MDOF) not-classically-damped structural systems controlled by Fluid Viscous Dampers (FVD) are investigated in a stochastic framework. The procedure consists of evaluation of the device optimal pattern by minimizing an objective function related to the dampers cost and subjected to a constraint on the structural behavior. For each configuration, the complete probabilistic characterization of the response is achieved by employing random vibration theory, Stochastic Linearisation (SL) techniques and a novel analytic model which provides closed-form PSD functions of earthquakes accelerations coherent to response spectra suggested by seismic codes. Exploiting this model, a procedure to speed up the Stochastic Linearisation technique by avoiding any numerical integration is proposed. Applications on MDOF building structures have been carried out to validate the proposed approach in terms of accuracy and reduction of the computational effort and to obtain optimal pattern of the passive control device coherently with the provisions of seismic building codes.

1. Introduction

The solution of a structural design problem generally requires the evaluation of a set of parameters in order to fulfill several requirements, for instance, in terms of strength, serviceability and dynamic performance of the structural system at hand. Each requirement is usually indicated as a limit state and the design problem, in other words, can be expressed as the measurement of the violation of a given set of limit states (Melchers, 1999). Since there are infinite sets of design parameters that ensure the respect of the limit states, optimization techniques may be deployed, in order to choose those parameters that satisfy the requirements and, at the same time, minimize a properly defined cost function.

Most of the established design strategies define structural safety in a deterministic way, assuming that both structural parameters and applied loads are known, even if conservative values, derived from statistical studies, are utilized. This approach leads to consider only the mean response and to neglect its dispersion. Since the uncertainties affect both structural properties and load characteristics, a more reliable analysis should be defined into a probabilistic framework. In the last decades, several methodologies have been developed for the probabilistic measure of the structural safety, in which any uncertainty about a design variable, a structural property or a load feature has to be taken into account explicitly and modeled through its respective probability density function (Melchers, 1999). Accordingly, also limit states and cost functions have to be described in terms of their probability of occurrence.

The dynamic response of structural systems subjected to seismic loads is often enhanced by introducing passive control devices, such as Fluid Viscous Dampers (FVD), Tuned Liquid Column Dampers (TLCD) or Non-linear Energy Sinks (NES). These devices operate through several different physical mechanisms by increasing the energy dissipation or by changing the dynamic characteristics of the system to which they are attached. Their use has received increasing attention in recent decades (Housner et al., 1997; Spencer and Nagarajaiah, 2003) and important applications for improving the structural performances to dynamic loads (e.g., earthquakes or winds) of new or existing building structures have been developed. The design parameters of passive control devices depend on the dynamic features of the structural system to be controlled as well as on the characteristics of the considered dynamic load. Moreover, some of the passive control devices exhibit non-linear constitutive laws and, even admitting that the primary system behaves linearly, in the controlled system a non-linear behavior may arise. This increases the computation difficulties and limits the large-scale use and design of these devices.

In fact, the probabilistic optimal design of non-linear passive control devices should be performed by means of Monte Carlo simulations, involving a very large computational effort (Oliva et al., 2017). On the other hand, in case of linear systems, the tools of random vibration theory allow for a full probabilistic characterization of the structural response, provided that a reliable stochastic model of the seismic input is available. Aiming at this, it is common to replace the non-linear equations of motion of a system equipped with a passive device with linear equivalent ones by using well-established procedures as Stochastic Linearisation (SL) techniques (Atalik and Utku, 1976; Roberts and Spanos, 1991; Elishakoff, 2000; Alibrandi and Ricciardi, 2012). The conditions of equivalence, when passing from the non-linear to the equivalent linear system, may be established in order to preserve some response quantities in statistical sense. Since the parameters of the linear equivalent system depend implicitly on response statistics, most of SL algorithms require the solution of a system of algebraic non-linear equations, although it has been found (Roberts and Spanos, 1991) that a simple recursive loop is adequate to simultaneously satisfy them. Hence, the computational burden required for the analyses increases, even if it is drastically reduced with respect to Monte Carlo simulations. Moreover, calculations are very often carried out only numerically, since analytical closed-form solutions for response statistics are available just for a limited class of problems (Artale et al., 2017). In Spanos and Miller (1994), formulae for the computation of the response spectral moments have been derived for the case of random excitations with band-limited white noise, Gaussian and Kanai-Tajimi seismic spectra. In order to overcome some limitations of the conventional SL, Fujimura and Der Kiureghian (2007) proposed an alternative method of linearisation, called “tail equivalent linearisation.” This is a non-parametric method which consists in replacing the non-linear system with a linear one, so that the tail probability of the linear response above a specified threshold corresponds to the first order reliability approximation of the tail probability of the non-linear response above the same threshold. It provides superior accuracy for the distribution of the maximum response, especially in the tail region and it was mainly used for reliability purposes (Der Kiureghian and Fujimura, 2009).

Alternatively, Giaralis and Spanos (2010) defined a stochastic dynamic-based algorithm in order to estimate the seismic demand of bilinear hysteretic SDOF oscillators consistently with seismic code provisions that does not require non-linear numerical integrations. Their algorithm consists in the definition of a non-parametric RS-consistent stationary PSD function and in the use of the SL in order to define the so-called equivalent linear parameters (ELPs) and, finally, in the estimation of the peak inelastic response of the non-linear oscillator. Since the applicability of this latter approach was limited to relatively mild non linear response, an higher-order SL scheme was further proposed in Spanos and Giaralis (2013) for the treatment of a wider class of hysteretic constitutive laws with a resulting higher accuracy. Recently, Mitseas et al. (2018) proposed a novel stochastic dynamics framework to estimate the peak inelastic response of MDOF strongly non-linear system in a seismic context without undertaking non-linear step-by-step integrations of the response. The algorithm allows for the seismic demand estimation of MDOF systems without numerical integrations nor modal combination rules involved. Starting again from the definition of a non-parametric RS-consistent PSD function, SL is used in order to decouple the MDOF system into several SDOF oscillators characterized by ELPs. These oscillators are able to capture the peaks of the non-linear response for each DOF of interest directly in the geometric space. In order to achieve high accuracy, the algorithm requires an iterative scheme in which, for each DOF, the PSD is updated basing on the RS defined by damping modification factors.

Among the several passive control devices proposed and realized in the last decades, Fluid Viscous Dampers (FVDs) have received great attention and have been widely used in order to reduce the effects of wind or earthquakes on civil structures and to mitigate the vibrations due to shocks in mechanical equipment. Their appeal for use in seismic engineering derives from the low maintenance required, from their re-usability for subsequent earthquakes, but also from the fact that the forces exerted by the dampers and elastic forces are out of phase and the stress level in the structure is not increased by their presence. A great amount of research papers have been devoted to the optimal design and optimal placement of fluid viscous dampers to enhance the structural performance. The most relevant scientific literature in this field has been recently collected in a very comprehensive review paper (De Domenico et al., 2019) which allows for a comparison of the different strategies used to identify the optimal design configurations of FVDs. Nevertheless, it is noteworthy to recall two approaches. In the first one (Tubaldi and Kougioumtzoglou, 2015), the non-stationary stochastic response of a hysteretic SDOF system equipped with FVDs is calculated by an approximate analytical technique that makes use of a modified SL scheme and allows to consider realistic seismic excitations with time-varying frequency content. In Gidaris and Taflanidis (2015) the performance assessment and optimal design of fluid viscous dampers in a probabilistic life-cycle cost framework is discussed to obtain optimal design under different seismic scenarios.

From a mathematical perspective, the procedure presented in this work belongs to the wider class of the constrained optimization problems. In particular, the optimal pattern of the device parameters is evaluated by minimizing an objective function related to the device cost and by ensuring that a constraint function based on the structural behavior is not violated. Both cost and constraint functions are defined into a probabilistic framework. For each damper configuration, the controlled system response is evaluated by using random vibration theory in conjunction with SL technique.

In order to reduce the great computational burden involved in these problems, two novelty aspects have been here proposed and introduced. Firstly, assuming that earthquake time-histories can be modeled as samples of a stationary stochastic process, an analytical representation of earthquake load Power Spectral Density (PSD) functions consistent with seismic codes Response Spectra (RS) (Barone et al., 2015, 2019) have been adopted. Secondly, an algorithm has been set up in order to obtain approximate analytical expressions of the response first spectral moments for not-classically damped Multi-degrees-of-freedom (MDOF) systems, without performing any numerical integration.

It is to remark that the more recent SL techniques for the determination of the seismic demand for hysteretic systems (Giaralis and Spanos, 2010; Spanos and Giaralis, 2013; Mitseas et al., 2018) can greatly benefit of these novelty aspects, both in terms of a significant reduction of the computational efforts in the derivation of RS-consistent PSD functions, and in accuracy, since some approximations in evaluating the response statistics can be removed without increasing the computational burden.

In the following, it will be shown how these spectral moments can be used in order to perform SL and to evaluate the optimal design of passive control systems in an efficient and accurate way. The paper is organized as in the following: in section 2 the probabilistic optimal design problem is firstly formulated in general form and then particularized for the case of n-DOF linear structural systems controlled by means of m concurrent non-linear FVDs (Di Paola et al., 2007; Di Paola and Navarra, 2009); in Section 3, in order to take advantage of the random vibration theory, the classical SL approach is described for the problem at hand and a procedure for the analytical evaluation of the response statistics, useful for SL technique, is proposed for linear n-DOF non-classically damped systems; section 4 is devoted to numerical applications in which the reduction in computational effort and the accuracy of the proposed procedure are investigated and the optimal design of FVDs is performed for a plane shear-type five-story frame and for a three-dimensional building structure. For this last application, the accuracy of the proposed procedure is further assessed in time-domain by performing a non-linear response history analysis on a set of spectrum compatible ground motion records. Finally, some conclusions are drawn. In Appendix brief details on the deriving of RS-consistent analytical PSD function and the expressions for its evaluation are provided, along with the analytical expressions that lead to the evaluation of the cross-spectral moments in modal space, once the direct spectral moments are determined.

2. Problem Formulation

The equations of motion of a n-DOF linear structural system in its so-called uncontrolled state, subjected to a sample of ground motion acceleration process Ü_g(t) can be expressed as:

$\begin{array}{ll}\text{M}\ddot{\text{U}}(t)+\text{C}\stackrel{\bullet }{\text{U}}(t)+\text{K}\text{U}(t)=-\text{M}\tau {\ddot{\text{U}}}_g(t)& (1)\end{array}$

where M, C and K are the (n × n) mass, damping and stiffness matrices, respectively, U(t) is the (n × 1) vector collecting the degrees of freedom of the structural system, dots means time derivatives and τ is the (n × 1) influence vector.

Aiming at reducing the dynamic response of the uncontrolled structure, it is common to introduce in the system passive control devices. The latter, operating through different physical mechanisms, generate additional damping forces or modify the dynamic characteristics of the so-called controlled system. Since many of the practically used passive control devices, such as Fluid Viscous Dampers (FVD), Non-linear Energy Sinks (NES) or Tuned Liquid Column Dampers (TLCD), present non-linear constitutive relationships, the general form of the equations of motion of the controlled system can be written as:

$\begin{array}{ll}\text{g}\left(\ddot{\widehat{\text{U}}},\stackrel{\bullet }{\widehat{\text{U}}},\widehat{\text{U}}\right)=\text{f}(t)& (2)\end{array}$

where $\widehat{\text{U}}$ is the new degree-of-freedom vector, which may differ from U(t) for those categories of devices that introduce additional degrees of freedom, for example passive absorbers; $g_i(\ddot{\widehat{\text{U}}},\stackrel{\bullet }{\widehat{\text{U}}},\widehat{\text{U}})$ and f_i(t) are the total internal non-linear forces and the external applied loads, respectively, acting in the i-th degree-of-freedom direction.

The dynamic behavior of the controlled system and its ability in mitigating the seismic response are governed by the design variables of the control devices, which, in turn, depend on both dynamic features of the uncontrolled system and on the characteristics of the considered dynamic load.

In general, the greater the size and cost of the used control devices, the greater reductions in response may be achieved, until allowance criteria provided by building codes are satisfied. Therefore, the problem of the optimal design of passive control devices can be properly set and, since earthquakes are random in nature, it should be tackle into a probabilistic framework, as in the following:

$\begin{array}{ll}\begin{array}{c}\begin{array}{c}min\\ \text{x}\end{array}\varphi (\text{x},\text{r})\\ \text{subjected to}:\\ P_s(\text{x},\text{r})-{\stackrel{-}{P}}_s\ge 0\\ \text{x}\in \Omega \end{array}& (3)\end{array}$

where ϕ(x, r) is the cost function to be minimized, x and r are the vectors collecting the design variables and the uncertain parameters, respectively, P_s(x, r) is the survival probability, $\overline{P_s}$ is the target survival probability and Ω is the feasibility domain of the design variables. Cost function and survival probability can be expressed in terms of design variables and of the response statistics, but their analytical expressions are specific for each kind of passive control device.

Generally, the uncertain parameters r can be divided into two categories. The first one is related to the definition of the structural model (uncertainty in mass, stiffness and damping values, or model uncertainties), whereas the second one accounts for the randomness of the load. However, in case of seismic input, it is possible to neglect the uncertainties of the structural model as they lead to smaller dispersions of the response (Pinto et al., 2007). Hereinafter, the system parameters are hence considered as deterministically known and x collects only the location patterns and the design variables of the control devices.

Moreover, it is assumed that earthquake acceleration time-histories may be modeled as finite time duration samples of a zero-mean Gaussian stationary stochastic process, completely defined by the knowledge of its Power Spectral Density (PSD) function. In this case, the vector r collects the parameters of the seismic input stochastic model, obtained by using recently proposed analytical expressions of PSDs consistent with assigned RS, that cover most of the international building codes (Barone et al., 2015, 2019). The Appendix reports further details of this PSD model along with the closed-form relationship between the RS parameters and the consistent PSD function ones. In recent studies (Giaralis and Spanos, 2010; Spanos and Giaralis, 2013), RS-consistent PSDs have been numerically derived and used also for stochastic analyses of non-linear yielding structures by the application of the SL. The joint use of such technique and an analytical model of the seismic PSD function could certainly improve the overall computational efficiency.

The solution of the problem expressed in Equation (3) requires, for each tentative set of the design variables, the stochastic analysis of a non-linear system, which is often performed by means of Monte Carlo simulations, involving very large computational efforts. On the other hand, in case of linear systems and a properly defined stochastic model of the seismic input, the probabilistic characterization of the structural response can be easily computed by means of the tools of stochastic analysis.

In the following, an optimal design problem is considered when FVDs are used as passive control devices. However, similar approaches may be addressed for other types of non linear passive control systems as, for instance, TLCDs (Di Matteo et al., 2014a,b, 2015) or NESs (Navarra et al., 2019b).

Viscous dampers have been widely used to mitigate the effects of wind or earthquakes on civil structures and in the shock and vibration isolation of equipment. Their appeal derives from the low maintenance required and their re-usability for subsequent earthquakes, but also from the fact that the forces exerted by the dampers are out of phase with respect to the elastic forces and do not increase the stress level in the structure. Moreover, they can be used for the protection of new constructions as well as for retrofitting purposes. Conversely, the major drawback in using viscous dampers consists in handling their non-linear force-velocity constitutive law.

The equations of motion of the controlled system in Equation (2), when m viscous dampers are concurrently deployed become:

$\begin{array}{ll}\text{M}\ddot{\text{U}}(t)+\text{C}\stackrel{\bullet }{\text{U}}(t)+\text{K}\text{U}(t)+{\text{F}}_D(t)=-\text{M}\tau {\ddot{\text{U}}}_g(t)& (4)\end{array}$

where F_D(t) is the vector of the non-linear forces exerted by the viscous dampers. Although in literature there are several attempts to model the constitutive law of viscous dampers by using the theory of visco-elasticity (Schwann et al., 1988) or the fractional calculus (Makris et al., 1993), most of the manufacturers currently use a force-velocity relationship, validated by several laboratory tests, expressed as:

$\begin{array}{ll}{f}_d(\stackrel{.}{Y})=C_d|\stackrel{.}{Y}{|}^{\alpha }\text{sign}(\stackrel{.}{Y})& (5)\end{array}$

being C_d and α the characteristic parameters of the damper device, Ẏ the relative velocity at the damper ends and sign(·) the signum function. For sesmic protection purposes, values of α between 0.15 and 0.50 are used, in order to attain quite large control forces even for small relative velocities and to have almost constant output forces for large velocity values.

The non-linear forces vector F_D(t) can be expressed as:

$\begin{array}{ll}{\text{F}}_D(t)={\text{R}}^{\text{T}}{\text{f}}_d(\stackrel{\bullet }{\text{Y}})& (6)\end{array}$

where Y(t) is a m-ranked vector that collects the relative displacements at the ends of each damper and all the response quantities whose statistics are useful for the computation of the cost function and of the survival probability. These quantities can be obtained as linear combinations of the degrees of freedom U(t), through the definition of a (m × n) transformation matrix R as:

$\begin{array}{ll}\text{Y}(t)=\text{R}\text{U}(t)& (7)\end{array}$

Since the selection of the degrees of freedom and of the response quantities of interest depends on the geometry of the problem and on the passive control devices locations, it is not possible to attain to a general expression of the matrix R. However, since FVDs are usually inserted into the frame braces, from a computational point of view, it is convenient to include in Y(t) all the inter-story drifts of the structure. The i-th element of the vector f_d (Ẏ) is expressed as in Equation (5), taking into account that each damper may have, in general, different characteristic parameters C_{d, i} and α_i. Obviously, if no dampers are deployed at the i-th inter-story, a value of C_{d, i} = 0 is set.

2.1. Cost Function and Survival Probability

In literature, several estimators of the cost function have been proposed (De Domenico et al., 2019). In Bahnasy and Lavan (2013), the use of the sum of the dampers constants C_{d, i} at the various floors has been proposed, whereas the expected value of the sum of the peak forces of each damper has been considered in Altieri et al. (2018) and Tubaldi et al. (2016). Herein, recalling the probabilistic aspects of the proposed approach, the cost function has been defined as the sum of the characteristic values of the peak force of each damper, that represents a reliable measure of its cost, being related to its dimensioning (Navarra et al., 2017). Hence, the cost function ϕ(x, r) in Equation (3) can be written as:

$\begin{array}{ll}\varphi (\text{x},\text{r})={\displaystyle \sum _{i=1}^m}{f}_{dk,i}={\displaystyle \sum _{i=1}^m}{C}_{d,i}|{\eta }_{k,i}{\sigma }_{{\stackrel{.}{Y}}_i}{|}^{{\alpha }_i}& (8)\end{array}$

where f_{dk, i} is the characteristic value (at 95% percentile) of the peak force exterted by the i-th damper, σ_Ẏi is the standard deviation of the relative velocity at the ends of the i-th damper and η_{k, i} is the correspondent peak factor, as defined in the classical first-passage reliability theory (Vanmarcke, 1972, 1975):

$\begin{array}{l}{\eta }_{k,i}\\ =\sqrt{2ln\left\{\frac{2{\nu }_{{\stackrel{.}{Y}}_i}{T}_s}{-ln(0.95)}\left[1-exp\left(-q_{{\stackrel{.}{Y}}_i}^{1.2}\sqrt{\pi ln\left[\frac{2{\nu }_{{\stackrel{.}{Y}}_i}{T}_s}{-ln(0.95)}\right]}\right)\right]\right\}}& (9)\end{array}$

In Equation (9), T_s is the duration of the time window, ν_Ẏi and q_Ẏi are the mean zero-crossing rate and the bandwidth factor, respectively, whose expressions can be evaluated in terms of the first spectral moments λ_{Ẏi, j} of the i-th relative velocity process:

$\begin{array}{ll}\begin{array}{c}{\nu }_{{\stackrel{.}{Y}}_i}=\frac{1}{2\pi }\sqrt{\frac{{\lambda }_{{\stackrel{.}{Y}}_i,2}}{{\lambda }_{{\stackrel{.}{Y}}_i,0}}};q_{{\stackrel{.}{Y}}_i}=\sqrt{1-\frac{{\lambda }_{{\stackrel{.}{Y}}_i,1}^2}{{\lambda }_{{\stackrel{.}{Y}}_i,2}{\lambda }_{{\stackrel{.}{Y}}_i,0}}}\end{array}& (10)\end{array}$

Spectral moments are defined as the geometric moments of the one-sided PSD function G_X(ω) with respect to the axis ω = 0, so that the m-th order spectral moment of a generic stochastic process X(t) is given by:

$\begin{array}{ll}{\lambda }_{X,m}={\displaystyle {\int }_0^{+\infty }}{\omega }^m{G}_X(\omega )\text{d}\omega .& (11)\end{array}$

Spectral moments, indeed, are related to peculiar statistics of stochastic processes and allow for their characterization. For example λ_{X, 0} and λ_{X, 2} represent the variances of the processes X(t) and Ẋ(t), respectively, and other quantities as central frequency and bandwidth parameter, as well as approximate solutions for the first-passage problem can be evaluated in terms of spectral moments (Vanmarcke, 1972, 1975, 1976b; Der Kiureghian, 1980; Di Paola and Muscolino, 1988).

The survival probability P_s(b_{max, i}, T_s) is associated to the non occurrence of crossings, into the time window T_s, of the i-th maximum allowable inter-story drift b_{max, i}, computed from the actual story height and can be evaluated as:

$\begin{array}{ll}{P}_s(b_{max,i},T_s)=\left[1-exp(-\frac{b_{max,i}^2}{2{\sigma }_{Y_i}^2})\right]exp(-2{\tilde{\alpha }}_{Y_i}(b_{max,i})T_s)& (12)\end{array}$

where the risk function ${\tilde{\alpha }}_{Y_i}(b_{max,i})$ is:

$\begin{array}{ll}{\tilde{\alpha }}_{Y_i}(b_{max,i})=2{\nu }_{Y_i}\frac{1-exp\left(-\sqrt{\frac{\pi }{2}}\frac{b_{max,i}}{{\sigma }_{Y_i}}{q}_{Y_i}^{1.2}\right)}{exp\left(\frac{b_{max,i}^2}{2{\sigma }_{Y_i}^2}\right)-1}& (13)\end{array}$

and the quantities ν_Yi, q_Yi and ${\sigma }_{Y_i}^2={\lambda }_{Y_i,0}$ are the mean zero-crossing rate, the bandwidth factor and the variance of the relative displacements, respectively. Therefore, they can be computed as in Equations (10), but with reference to the process Y_i, in terms of the first spectral moments λ_{Yi, j}. Assuming that the failure condition is attained when only one inter-story drift exceeds the allowable value, the global survival probability P_s in Equation (3) is finally obtained as:

$\begin{array}{ll}{P}_s=min\left\{P_s(b_{max,i},T_s)\right\}& (14)\end{array}$

3. Efficient Stochastic Linearisation Technique

Since Equation (4) is non-linear, the evaluation of the response statistics useful for solving the optimal design problems has to be performed through Monte Carlo simulations, which require heavy computational efforts. In order to overcome this difficulty, the Stochastic Linearisation (SL) technique may be an effective tool (Atalik and Utku, 1976). The basic idea of SL is to replace the original non-linear system in Equation (4) with an equivalent linear one:

$\begin{array}{ll}{\text{M}}^{(e)}\ddot{\text{U}}(t)+{\text{C}}^{(e)}\stackrel{\bullet }{\text{U}}(t)+{\text{K}}^{(e)}\text{U}(t)=\text{f}(t)& (15)\end{array}$

in which the equivalent system matrices M^(e), C^(e) and K^(e) are evaluated by minimizing the difference between the two systems in statistical sense. The expressions of equivalent linear matrices for MDOF systems equipped with several kind of passive control devices, such as Tuned Liquid Column Dampers and Non-linear Energy Sinks, may be found in Navarra et al. (2019a). In the case of FVDs, it can be shown that the equivalent linear mass and stiffness matrices coincide with those of the uncontrolled system (i.e., M^(e) = M and K^(e) = K), while the equivalent linear damping matrix C^(e) can be obtained as:

$\begin{array}{ll}{\text{C}}^{(e)}=\text{C}+{\text{R}}^{\text{T}}{\text{D}}_{FVD}\text{R}& (16)\end{array}$

in which R is the (m × n) transformation matrix, whereas the diagonal matrix D_FVD can be expressed as (Di Paola et al., 2007; Di Paola and Navarra, 2009):

$\begin{array}{l}{D}_{FVD,ij}=\text{E}\left[\frac{\partial f_{d,i}}{\partial {\stackrel{.}{Y}}_j}\right]=\\ \alpha {\hat{C}}_{d,j}\frac{2^{\alpha /2}\Gamma (\alpha /2)}{\sqrt{2\pi }}{\sigma }_{{\stackrel{.}{Y}}_j}^{\alpha -1}{\delta }_{ij},(i,j=1,2,\dots ,m)& (17)\end{array}$

being Γ(·) the Euler Gamma function, δ_ij the Kronecker delta and σ_Ẏj = λ_{Yj, 2} the standard deviation of the j-th relative velocity.

It is to remark that Equation (17) is derived based on a statistical equivalence in terms of damper force and by assuming the Gaussianity of the response process. Recently, other different equivalent damping formulae based on energy equivalency or by assuming other non-Gaussian probability distributions have been proposed (De Domenico and Ricciardi, 2018, 2019). However, in all these approaches the equivalent linear system is completely defined when some response statistics are evaluated. This is, in general, achieved by using an iterative procedure. In the first iteration, it is assumed that the equivalent linear system coincides to the uncontrolled system whereas, at subsequent iterations, the estimations of equivalent linear matrices computed at the previous iteration are considered.

In conclusions, it appears that the optimal design problem into a probabilistic framework requires the evaluation in a efficient way of the first spectral moments of the response process. Furthermore, even assuming that the uncontrolled system, Equation (1), may be considered classically damped, the presence of passive control devices makes the controlled system a non-classically damped one. In this context, in order to determine the response spectral moments, two approaches may be followed. In the most common one the evaluations are carried out through numerical integrations in the geometric space, accordingly to the flowchart reported in Figure 1A. In this case, the computational burden required for the analyses increases, even if it is drastically reduced with reference to Monte Carlo simulations. In the second alternative approach, herein proposed, the computations of spectral moments, taking advantage of the analytical model of the seismic action, does not require any numerical integrations, aiming at drastically reducing the computational efforts. A flowchart of this procedure is reported in Figure 1B and these two approaches are addressed in the following subsection.

FIGURE 1

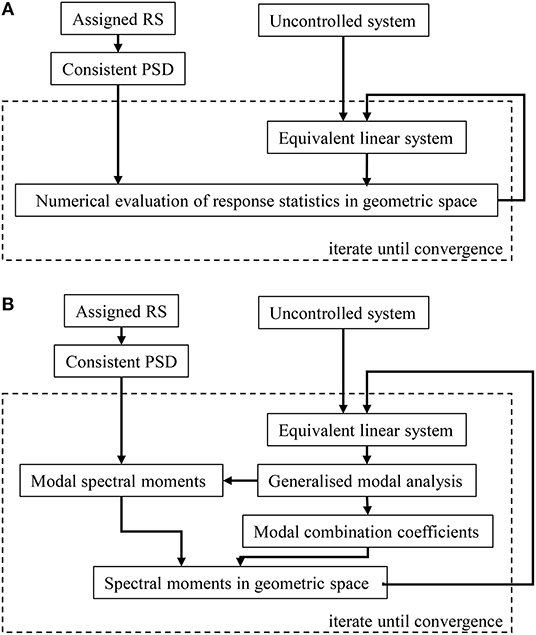
Figure 1. Flowchart for Statistical Linearisation technique. (A) Numerical approach. (B) Proposed procedure.

3.1. Numerical Approach for the Evaluation of Spectral Moments

The evaluation of the j-th order spectral moment matrix in terms of the response quantity of interest vector Y may be performed through numerical integration in the geometric space of the response PSD matrix:

$\begin{array}{ll}{\Lambda }_{\text{Y},j}=\text{R}\left({\displaystyle {\int }_0^{\infty }}{\omega }^j{\text{G}}_{\text{U}\text{U}}(\omega )d\omega \right){\text{R}}^{\text{T}}& (18)\end{array}$

being G_UU(ω) the one-sided PSD matrix of the response:

$\begin{array}{ll}{\text{G}}_{\text{U}\text{U}}(\omega )={\text{H}}^{*}(\omega ){\text{M}}^{(e)}\tau {\tau }^{\text{T}}{\text{M}}^{(e)\text{T}}{\text{H}}^{\text{T}}(\omega )G_{{\ddot{\text{U}}}_g}(\omega )& (19)\end{array}$

in which H(ω) = [−ω²M^(e) + iωC^(e) + K^(e)]⁻¹ is the transfer functions matrix, the asterisk denotes complex conjugate and G_Üg(ω) is the seismic load PSD function, whose expression is reported in Appendix for seismic actions consistent with several building codes RS. The spectral moments for the evaluation of the equivalent linear system, for the computation of the cost function and for the determination of the survival probability may be properly extracted from Λ_{Y, j}.

For lightly damped and flexible systems (large period of vibration), the accuracy of Equation (18) decreases mainly due to an insufficiently long duration assumed for the stationary excitations so that the steady-state conditions are not met. In order to enhance the accuracy, a frequency-dependent corrective damping factor can be adopted (Vanmarcke, 1976a). Spanos and Giaralis (2013) provided numerical results to facilitate the selection of sufficiently long duration of stationary excitation as a function of the structural natural frequency and damping ratio.

Numerical integration of Equation (18) requires large computational efforts and may lead to inaccurate estimations of spectral moments, due to the very sharp functions involved in the case of low damping values. Since numerical integrations are required at each step of the SL, the approach above described is highly time consuming, especially when used into an optimization problem.

3.2. Analytical Evaluation of the Spectral Moments

Generally, the equivalent linear system is not classically damped and a generalized modal analysis needs to be applied. Equations of motion, as customary, can be reformulated into a set of 2n first-order differential equations:

$\begin{array}{ll}\stackrel{\bullet }{\text{Z}}={\text{D}}^{(e)}\text{Z}+\text{V}{\ddot{\text{U}}}_g(t)& (20)\end{array}$

where the state-variables vector Z, the system matrix D^(e) and the load vector V are defined as:

$\begin{array}{ll}\begin{array}{ccc}\text{Z}=\left[\begin{array}{c}\text{U}\\ \stackrel{\bullet }{\text{U}}\end{array}\right],& {\text{D}}^{(e)}=\left[\begin{array}{cc}0& {\text{I}}_n\\ -{\text{M}}^{(e)-1}{\text{K}}^{(e)}& -{\text{M}}^{(e)-1}{\text{C}}^{(e)}\end{array}\right],& \text{V}=-\left[\begin{array}{c}0\\ \tau \end{array}\right]\end{array}& (21)\end{array}$

The eigenvalues square roots γ_i and the eigenvectors ψ_i of D^(e) occur in conjugate pairs and they can be collected in such a way that ${\gamma }_i={\gamma }_{i+n}^{*}$ and ${\psi }_i={\psi }_{i+n}^{*}$. Moreover, due to the structure of the state-variables vector, the i-th eigenvector and the modal matrix are:

$\begin{array}{ll}\begin{array}{cc}{\psi }_i=\left[\begin{array}{c}{\varphi }_i\\ {\gamma }_i{\varphi }_i\end{array}\right],& \text{Ψ}=\left[\begin{array}{cccc}{\psi }_1& {\psi }_2& \cdots & {\psi }_{2n}\end{array}\right]=\left[\begin{array}{cc}\Phi & {\Phi }^{*}\\ \Gamma \Phi & {\Gamma }^{*}{\Phi }^{*}\end{array}\right]\end{array}& (22)\end{array}$

where Γ = diag{γ₁, γ₂, ⋯ , γ_n} and Φ = [ϕ₁, ϕ₂, ⋯ , ϕ_n] are the diagonal matrix of the eigenvalues square roots and the reduced modal matrix in terms of only displacements, respectively. Lastly, the modal participation factors vector can be defined as p = Ψ⁻¹V. The i-th eigenvalue square root can be rewritten as γ_i = −ζ_iω_0i±iω_Di, where ω_0i, ω_Di and ζ_i are determined by:

$\begin{array}{ll}\begin{array}{ccc}{\omega }_{0i}=\left|{\gamma }_i\right|,& {\zeta }_i=-\frac{\text{Re}\left[{\gamma }_i\right]}{\left|{\gamma }_i\right|},& {\omega }_{Di}={\omega }_{0i}\sqrt{1-{\zeta }_i^2}\end{array}& (23)\end{array}$

These parameters designate natural frequency, modal damping and damped frequency of the i-th modal oscillator (Igusa et al., 1984), respectively. Taking advantage by the analytical definition of the seismic input PSD function reported in Appendix, it is possible to perform a closed-form approximate evaluation of direct spectral moments in the modal space, without resorting to numerical integrations (Barone et al., 2019). Referring to the i-th modal oscillator response process Q_i(t), the expression of the j-th spectral moment λ_{j,Qi, k} is:

$\begin{array}{ll}{\lambda }_{j,Q_i,k}=\frac{G_{{\ddot{\text{U}}}_g}({\omega }_{0i})}{4{\zeta }_i{\omega }_{0i}^{3-j}}{\phi }_{j,k}+\frac{1}{{\omega }_i^4}{\displaystyle \sum _{s=1}^{k-1}}{G}_{{\ddot{\text{U}}}_g}({\omega }_s){\omega }_s^{j+1}{\gamma }_{j,s}& (24)\end{array}$

when ω_0i falls within the k-th branch of the input PSD (see Equation 32), while the dimensionless quantities φ_{j, k} and γ_{j, s} are defined as follows:

$\begin{array}{l}{\phi }_{j,k}=\pi -\frac{4{\zeta }_i}{(1+j)(1+j+e_k)}\{\begin{array}{ll}{e}_k& j=0,2;\\ 2(1+e_k)& j=1;\\ 8+3e_k& j=3;\end{array}\\ {\gamma }_{j,s}=\frac{e_{s+1}-e_s}{(1+j+e_{s+1})(1+j+e_s)}& (25)\end{array}$

and the quantities e_i, ω_s and G_Üg(ω_s) are the parameters of the analytical model of the PSD function, whose meaning is detailed in the Appendix. Further details on the derivation and application of Equations (24) to (25) can be found in Barone et al. (2019).

Di Paola and Muscolino (1988) demonstrated that the cross-spectral moments of any order λ_{j,Qi, Qk}, if they exist for a given PSD function of the excitation, may be obtained recursively as linear combinations of the direct spectral moments. These analytical expressions are reported in the Appendix for the sake of simplicity. Furthermore, it is noted that equations from (20) to (23) account for unitary values of modal participation factors p. In this way, closed-from expressions for the determination of modal spectral moments—like those in Equation (24)—can be used straightforwardly. Conversely, when analytical expressions are not available for the problem at hand, only a limited number of numerical integrations should be performed in the modal space. Once the cross-spectral moments of the modal oscillators are obtained, the j-th order spectral moment of a set of quantities of interest in the geometric space defined by the vector Y can be computed as (Igusa et al., 1984):

$\begin{array}{r}{\lambda }_{Y_r,j}={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^n}(C_{r,ik}\text{Re}\left[{\lambda }_{j,Q_i,Q_k}\right]-D_{r,ik}\text{Im}\left[{\lambda }_{j+1,Q_i,Q_k}\right]+\\ E_{r,ik}\text{Re}[{\lambda }_{j+2},Q_i,Q_k])& (26)\end{array}$

where the modal combination coefficients C_{r, ik}, D_{r, ik}, and E_{r, ik}, which depend on the modal participating factors, can be determined as:

$\begin{array}{ll}\begin{array}{ccc}{C}_{r,ik}=a_{ri}{a}_{rk},& D_{r,ik}=a_{ri}{c}_{rk}-a_{rk}{c}_{ri},& E_{r,ik}=c_{ri}{c}_{rk}\end{array}& (27)\end{array}$

being a_ri and c_ri the entries of the following matrices:

$\begin{array}{ll}\begin{array}{cc}\text{a}=-2\text{Re}\left[\text{b}{\Gamma }^{*}\right],& \text{c}=-2\text{Re}\left[\text{b}\right]\end{array}& (28)\end{array}$

whereas the matrix b = RΦp_n, with p_n = diag{p₁, p₂, ⋯ , p_n}.

It is worth to note that this procedure can be generally applied for both classically and non-classically damped systems and it can be easily implemented in a computer program routine. In general, approximate evaluations of the spectral moments are achieved since analytical closed-form solutions for response statistics are available just for a limited class of problems (Spanos and Miller, 1994; Artale et al., 2017). In these cases, exact analytical evaluation of the direct spectral moments in the modal space may be used in place of the Equation (24), thus obtaining exact results. Ultimately, the evaluation of spectral moments of response quantities of interest needs only the estimation of $4\widehat{n}$ direct spectral moments in modal space, if a modal truncation is applied and only $\widehat{n}\le n$ modal contributions are retained. The estimation of the spectral moments λ_{Yr, j} allows for the updating of the linear equivalent system, for the estimation of the cost function and for the evaluation of the survival probability, as described in the previous section 2.

4. Numerical Applications

In this section, aiming to show the validity of the proposed approach, the results of numerical applications are reported. Case studies of optimal design of fluid viscous dampers are addressed for a plane five-story shear-type frame and for an irregular three-dimensional building structure.

Firstly, it is to be remarked that the analytical procedure proposed in section 3.2 is based on the approximate evaluation of the direct modal spectral moments, Equations (24 and 25), by taking advantage of the definition of the probabilistic analytical model of the seismic input reported in Appendix. The same approach would also apply for other environmental hazards, i.e., wind or ocean waves, when a PSD model of the input is available. The issue of accuracy of the seismic PSD analytical model has been investigated in Barone et al. (2019), to which the reader is referred for further details. In Figure 2, however, a comparison between first order closed-form spectral moments (m = 0, 1, 2) and their numerical counterparts is shown for several values of natural periods and viscous damping ratios. Results are in very good agreement and small differences can be observed for high-order moments at large natural periods and damping ratios.

FIGURE 2

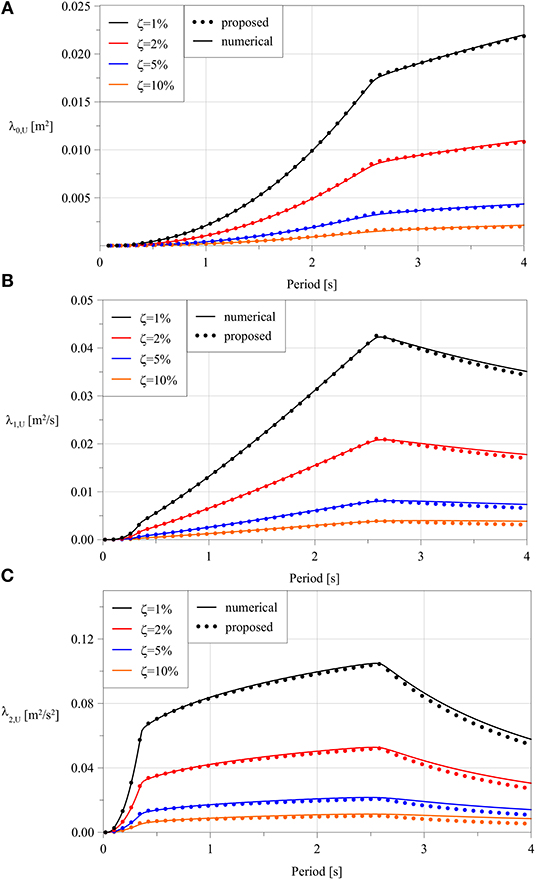
Figure 2. Comparison between the first spectral moments evaluated numerically (solid lines) and by closed-form approximate expressions (dots) against natural period. (A) Zero order moments. (B) first order moments. (C) second order moments.

Therefore, when a specific application needs the evaluation of spectral moments in those cases in which larger errors can be anticipated, an alternative approach may consist in using numerical integration only for the 4n first direct modal spectral moments, instead of Equations (24, 25), and in evaluating all other response statistics accordingly to section 3.2. In this way both computational efficiency and high accuracy may be obtained.

In all the following numerical applications. the seismic load is modeled accordingly to RS prescribed by Eurocode 8 (UNI ENV 1998:2005, 2005). In particular, it has been modeled as a process having an EC8-compatible PSD function, obtained considering the ground type A and a pseudo-stationary duration T_s = 20 s. Nevertheless, similar results can be obtained for a wide range of building codes RS covered by the model adopted (Barone et al., 2015, 2019). In Table 1, the parameters used to define the RS and the correspondent values in PSD analytical model, are reported.

TABLE 1

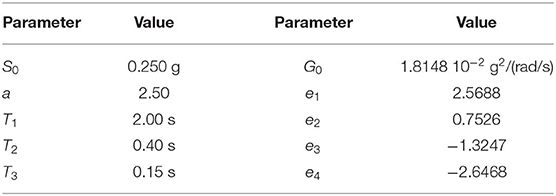
Table 1. Parameters for the definition of the design earthquake in terms of Response Spectrum and PSD function.

Lastly, it is worthwhile noting that, since viscous dampers are usually installed in the braces of the structural frames, the relative displacements at the damper ends constitute a subset of the inter-story drifts at each story and in each direction. Therefore, it is convenient to denote with Y(t) the vector of all the inter-story drifts, to evaluate R accordingly, and to set the parameters C_{d, i} = 0 for all the locations in which actually there are no dampers.

4.1. Accuracy and Computational Efficiency

In order to investigate the proposed procedure both in terms of accuracy and computational efficiency, a plane five-story shear-type frame, originally proposed in Takewaki (1997) and then modified in Trombetti and Silvestri (2004) has been considered. In this structural system, referred to as Model 1, both horizontal stiffness of the columns and the story mass do not vary along the height. In particular, the mass and stiffness at each floor are $m_i=8·10^4$ kg and $k_i=4·10^7$ N/m, respectively. It is also assumed a constant modal damping ratio ζ_i = 0.02 and the horizontal displacements U_i at each story have been chosen as degrees of freedom. The location vector is given as τ = [1 1 1 1 1]^T. In this application, the inter-story drifts are obtained as Y(t) = RU(t), where the linear transformation matrix R is:

$\begin{array}{ll}\text{R}=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ -1& 1& 0& 0& 0\\ 0& -1& 1& 0& 0\\ 0& 0& -1& 1& 0\\ 0& 0& 0& -1& 1\\ \end{array}\right]& (29)\end{array}$

As a first application, two identical FVDs having α_i = 0.15 and $C_{d,i}=1\times 10^5{\mathrm{\text{N/(m/s)}}}^{{\alpha }_i}$ and positioned only at the first and third inter-story, are considered. Stochastic linearisation is performed using four statistical equivalences criteria, chosen among those described in De Domenico and Ricciardi (2018). In particular, force-based Gaussian SLT (FB-G), force-based non-Gaussian SLT (FB-NG), equal energy Gaussian SLT (EE-G) and equal energy non-Gaussian SLT (EE-NG) criteria are used. Response statistics are computed for uncontrolled and controlled system and, in the latter case, for each of the aforementioned equivalence criteria. Results are reported in Table 2 in terms of computational time and of mean relative errors in the evaluation of the displacements, U_i and relative velocity standard deviations Ẏ_i. The two mean errors are defined as follows:

$\begin{array}{l}{ē}_U=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\frac{{\sigma }_{U_i,ana}-{\sigma }_{U_i,num}}{{\sigma }_{U_i,num}};\\ {ē}_{\stackrel{.}{Y}}=\frac{1}{m}{\displaystyle \sum _{i=1}^m}\frac{{\sigma }_{{\stackrel{.}{Y}}_i,ana}-{\sigma }_{{\stackrel{.}{Y}}_i,num}}{{\sigma }_{{\stackrel{.}{Y}}_i,num}}& (30)\end{array}$

where the subscripts ana and num stand for analytical and numerical evaluation, respectively.

TABLE 2

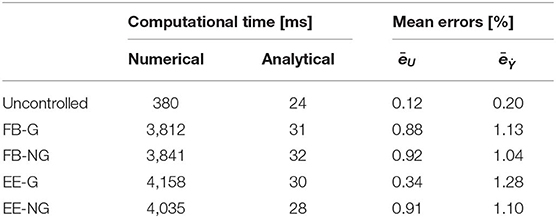
Table 2. Computational times and mean errors for application of numerical and analytical procedures.

Outcomes of computational times for uncontrolled system show that a great reduction of more than 90% is achieved for each evaluation of response statistics, whereas the mean errors with respect to numerical integrations, in terms of both displacements and relative velocities, are negligible.

The advantage in using analytical procedure becomes more and more evident when it is used inside a SL procedure. In fact, for the present case, eleven iterations are needed, irrespective of the equivalence criterion adopted; the computational efforts of the numerical approach increase proportionally, while no significant increments of computational time are observed for the analytical procedure. During the iterations, discrepancies due to the use of analytical procedure tend to accumulate, but the mean errors are limited below few percentage points.

4.2. Optimal Patterns and Optimal Design

In this section, the proposed analytical procedure is applied to determine the optimal pattern of fluid viscous dampers, accordingly to the minimization problem outlined in Equation (3). The minimization procedure is carried out by using the routine fmincon in MATLAB environment that uses the interior-point algorithm. Following this approach, the constrained minimization is reduced to a sequence of approximate minimization problems (Byrd et al., 2000).

The probabilistic constraint in the optimization loop is defined by assuming that structure fails when the maximum inter-story drift ratio at any story and in any direction exceeds the value of 0.5%, as suggested by Eurocodes. Such a value ensures almost elastic behavior of the structure. The minimum allowable survival probability ${\bar{P}}_s$ is treated as a parameter and numerical analyses are performed for different values of ${\bar{P}}_s$.

With reference to the aforementioned Model 1, the optimal design of viscous dampers is performed by considering the presence of a device at each floor and assuming a constant story height h_i = 3.50 m. Optimal patterns have been evaluated for several values of the dampers coefficient α, ranging from 0.15 to 1.00, and for two values of the target survival probability ${\bar{P}}_s$, 0.90 and 0.98. Figure 3 depicts the cost function of Equation (8) against α, whereas the correspondent optimal values of C_{d, i} are shown in Figure 4.

FIGURE 3

Figure 3. Cost function for ${\bar{P}}_s=0.90$ and ${\bar{P}}_s=0.98$.

FIGURE 4

Figure 4. Optimal pattern of viscous dampers. for (A) ${\bar{P}}_s=0.90$ and (B) ${\bar{P}}_s=0.98$.

It is worth to note that, for every value of α, the optimal pattern remains practically the same and the presence of dampers at fifth inter-story is excluded (i.e., C_{d, 5} = 0). Moreover, the use of strongly non linear devices has proven to be beneficial as it allows for a great reduction of the maximum forces exerted by dampers, thus reducing their size and, consequently, their cost.

In Figure 5, cumulative distribution functions of the inter-story drifts have been computed for probability values from 1% to 99% and compared with the maximum allowable drift (0.5% of the inter-story height). For the uncontrolled structural system (Figure 5A), i.e., when no dampers devices are used, all inter-story drifts largely exceed the limit, whereas Figures 5B,C depict the configurations correspondent to the optimal deployment of viscous damper devices for α = 1.00 and α = 0.30, respectively. In the latter configurations, optimal control of structural displacements is achieved, since most of inter-story drifts reach the maximum allowable value at the same time, thus obtaining an almost uniform distribution of deformations and stresses throughout the height of the frame (Connor, 2003).

FIGURE 5

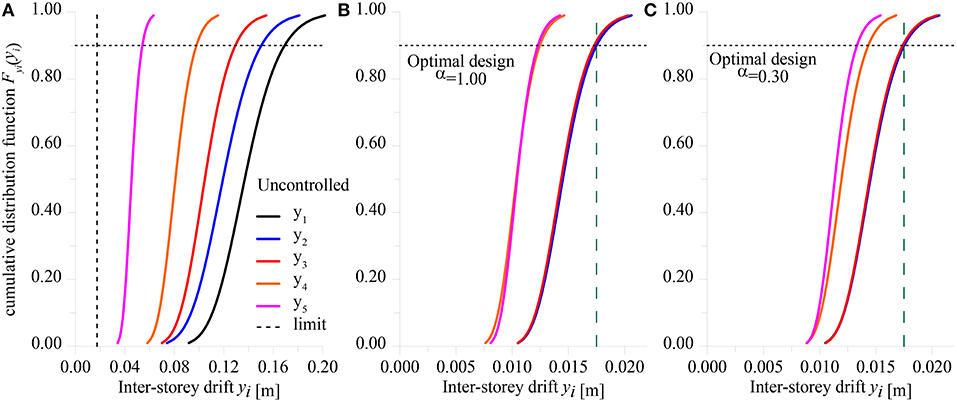
Figure 5. Cumulative distribution functions of inter-story drifts. (A) Uncontrolled structure. (B) optimal design for α = 1.00. (C) optimal design for α = 0.30. Target survival probability ${\bar{P}}_s=0.90$.

The second structural model, denoted as Model 2, consists of an irregular three-dimensional six-story building structure, whose geometrical characteristics are illustrated in Figure 6. Each floor height is 4.00 m, the first three floors have an overall dimension of 8.0 m by 16.0 m, while the top three story have plan dimension of 8.0 m by 8.0 m. All the columns are made up by HE400A profiles, whereas beams have IPE360 cross section. An uniform gravity load of q = 5.5 kN/m² is considered. This structure is representative of a low-to-medium rise civil steel building. Under the assumptions of rigid diaphragms at each floor and of inextensible columns, the dynamically significant degrees of freedom of the i-th floor can be reduced to two translations (u_i and v_i) and a rotation φ_i, for a total of 18 degrees of freedom. A constant modal damping of ζ_i = 0.02, (i = 1, …, 6) is assumed.

FIGURE 6

Figure 6. Geometrical characteristics of the six-story three-dimensional building.

The structure is composed of two frames in x-direction and of three frames in y-direction. In this case, the vector Y collects all the 27 inter-story drifts (six for the frames X1, X2, Y1, and Y2 and three for the frame Y3), useful for evaluate the constraint function and the R matrix is derived accordingly.

The first columns of the Table 3 reports the modal parameters of the stiffer modal oscillators in terms of natural frequencies and of mass participating ratios for two epicentral directions of the ground motion, namely θ = 0° (x-direction) and θ = 90° (y-direction). For each frame, Figure 7 depicts the distribution of inter-story drifts peak values along the height computed for 25%, 50% (mean value), 75% and 90% percentiles. It can be observed that the building exhibits inter-story drift ratios that exceed the value of 0.5% for both the epicentral directions, even if these are larger when earthquake strikes in y-direction.

TABLE 3

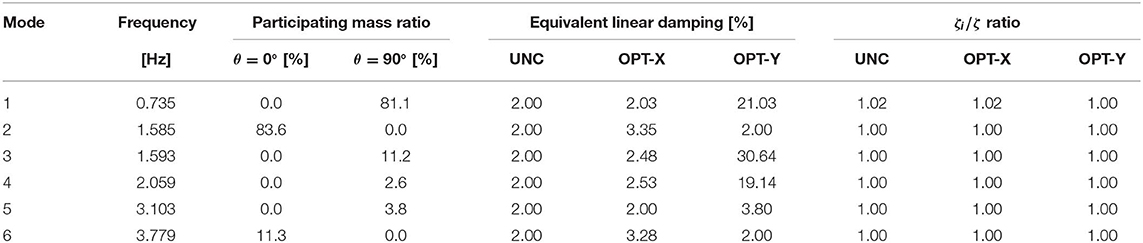
Table 3. Natural frequencies, mass participation ratios and equivalent linear damping of Model 2 system.

FIGURE 7

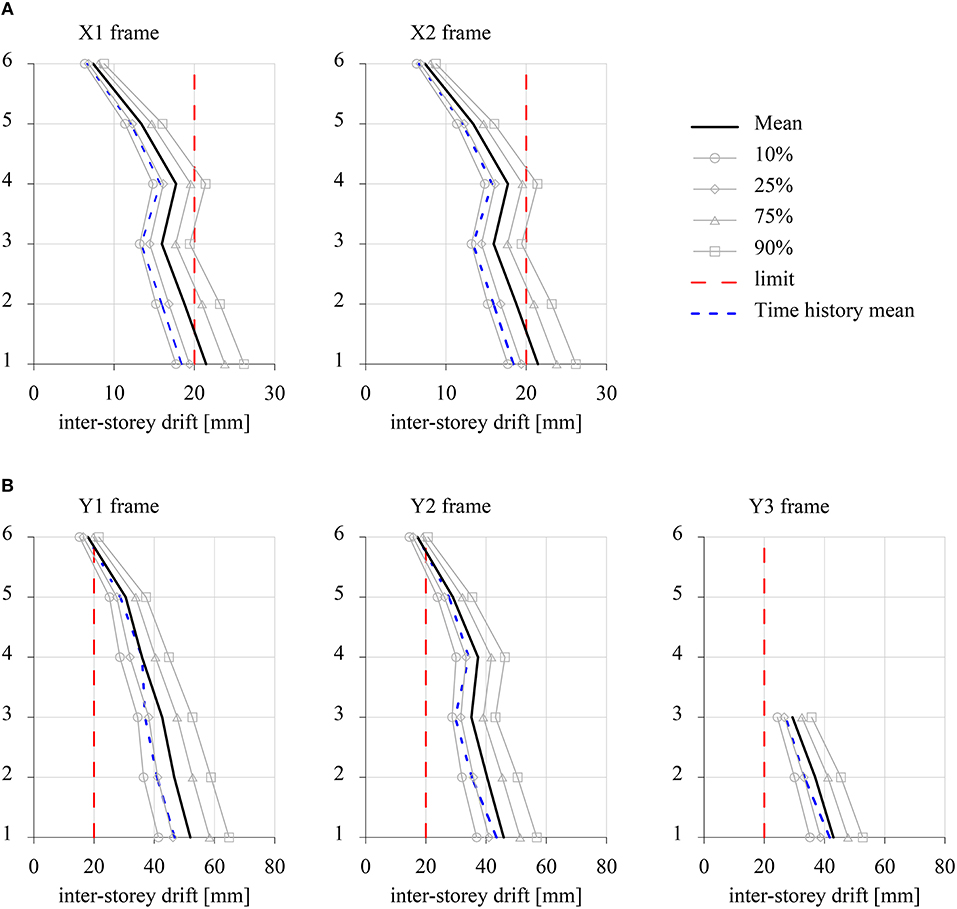
Figure 7. Peak values of inter-story drifts of the Model 2 uncontrolled system. (A) θ = 0°. (B) θ = 90°.

Four typologies of dampers are considered for optimization purposes, all having the non-linear coefficient α = 0.3. In particular, the characteristic parameters of the dampers at the three lower floors of x-direction and y-direction frames have been denoted as C_{d, xl} and C_{d, yl}, respectively, whereas the correspondent parameters of the dampers at the three higher floors have been denoted as C_{d, xh} and C_{d, yh}, respectively.

Two analyses have been performed in order to evaluate the optimal pattern of the viscous dampers for a target survival probability of ${\bar{P}}_s=0.90$ and for θ = 0° (OPT-X) and θ = 90°(OPT-Y). In Table 4, the cost function and the values of the characteristic parameters of the four damper typologies are reported for θ = 0° and θ = 90°. It is to be noted that, irrespective of the epicentral direction, the optimal damper configurations require dampers only at lower floors, since the dynamic behavior of the building structure is dominated by the first bending mode. Table 4 also shows that the maximum inter-story drift occurred at the first floor of X1 frame for θ = 0° and at the first floor of Y1 frame for θ = 90°. Moreover, in the last columns of Table 3 the values of equivalent linear damping at each of the first six modes are reported for uncontrolled system (UNC) and for the optimal configurations attained for θ = 0° (OPT-X) and θ = 90° (OPT-Y). The corrective damping ratios ζ_i/ζ (Spanos and Giaralis, 2013), also reported in Table 3, show that, for the problem at hand, the stationarity assumption has negligible effects in the determination of the response statistics. Since optimal design leads to inter-story drifts close to the limit value, larger dampers are required in y-directed frames. This is obviously reflected also in equivalent linear damping values. Figure 8 depicts the distribution along height of the peak values of the inter-story drifts resulting from the optimal design for the epicentral directions θ = 0° and θ = 90°.

TABLE 4

Table 4. Cost function and characteristic parameters for optimal configurations.

FIGURE 8

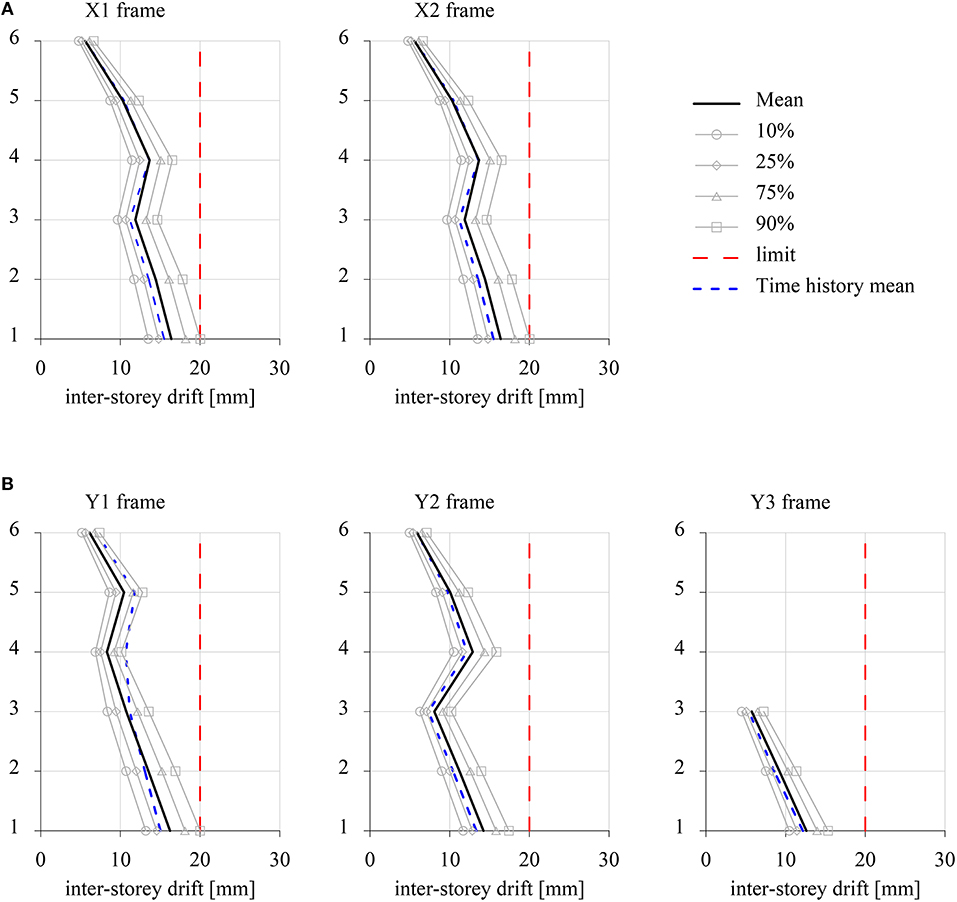
Figure 8. Peak values of inter-story drifts of the Model 2 in its optimal controlled configuration. (A) θ = 0°. (B) θ = 90°.

Since the proposed approach contains several approximations (mainly related to the modeling of the seismic action and on the use of SL), its effectiveness in determining the optimal configuration of dampers is further assessed in the time domain. Aiming at this, a set of seven natural recorded ground motion time-histories has been selected in order to match the EC8 RS used in the previous analyses (Iervolino et al., 2010). Individual ground motion records have been scaled and the spectrum compatibility has been achieved by imposing a ±10% tolerance with respect to the target RS in the period range between 0.10 and 2.5 s. In Table 5, all the selected records are listed, together with the main characteristics of the considered earthquakes. The results of the spectrum-compatibility check are shown in Figure 9 in terms of individual and mean RS together to the target RS and the tolerance zone.

TABLE 5

Table 5. Characteristic of selected ground motion records.

FIGURE 9

Figure 9. Spectrum compatibility check results.

Equations (1) and (4) have been solved by means of a step-by-step fourth-order Runge-Kutta integration scheme in order to evaluate the dynamic response of the Model 2 building subjected to the selected ground motions for the two epicentral directions θ = 0° and θ = 90°. Peak values of the inter-story drift have been computed for each record and their mean value has been reported in blue dashed line for comparison purposes in Figure 7 and Figure 8 for uncontrolled and optimal controlled configurations, respectively. The comparison in the uncontrolled system shows that, although stochastic analysis tends to overestimate the inter-story drifts, both the methodologies are able to capture the distribution of the inter-story drift along the height of the building. Also for the optimal damper configuration cases, the time-domain analysis shows a good agreement with the results of the stochastic analysis, thus demonstrating the effectiveness of the proposed approach in the optimal design of a passive control system. However, it is to be remarked that the time-domain analysis allows to evaluate only the mean values of the response peaks, whereas the stochastic analysis provides the full probabilistic characterization of the response.

5. Conclusions

In this paper, a methodology for the optimal design of passive control systems into a probabilistic framework has been described. In this way, uncertainties and response dispersion have been taken into account and, at the same time, a seismic analysis consistent with the Eurocode 8 response spectra has been carried out. The following conclusions can be drawn:

• A general form of Stochastic Linearisation approach for the cases of MDOF structural systems controlled by multi concurrent passive control devices has been presented and an iterative efficient solution, able to avoid any use of numerical integrations, has been proposed for the case of seismic loads.

• Herein, an optimal design procedure for fluid viscous dampers has been formulated. For this purpose, a cost function has been used as objective function to minimize. This has been defined as the sum of the characteristic values of the forces exerted by the dampers themselves.

• Taking advantage of an analytical model for the computation of response spectra compatible PSD functions as well as of complex modal analysis in state-space, analytical evaluations of the first spectral moments of a set of response quantities of interest have been derived for not-classically damped systems.

• The design problem has been posed in terms of survival probability considering that the failure of the structural system is identified with the over-crossing of a maximum allowable relative displacement.

• The validity of the proposed approach has been investigated in terms of accuracy and computational efficiency and two applications have been presented. The first one is related to a plane shear-type five-story frame, while the second one deals with a six-story three-dimensional building structure. Optimal damper configurations and cumulative distribution functions of inter-story drifts have been evaluated and it is proved that the proposed procedure leads to an accurate evaluation of response statistics.

• The proposed procedure allows for a dramatic reduction of the computational time, especially when is used for those problems that make intensive use of stochastic linearisation technique, as optimal design of passive control device.

• The effectiveness of the proposed approach has been assessed against the results of time-domain analyses by using a set of seven scaled spectrum-compatible natural ground motion records.

• The most recent SL techniques for the hysteretic systems seismic demand evaluation can benefit of the two novel aspects herein presented, namely the analytical model of PSD functions and the algorithm for evaluating spectral moments, in terms of both computational efficiency and accuracy.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All the authors contributed in an equal manner to the study of the relevant literature, to the derivation of the proposed approach, to the preparation of software routines for the numerical applications and to writing and editing of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alibrandi, U., and Ricciardi, G. (2012). Stochastic Methods in Nonlinear Structural Dynamics. Vienna: Springer.

Google Scholar

Altieri, D., Tubaldi, E., De Angelis, M., Patelli, E., and Dall'Asta, A. (2018). Reliability-based optimal design of nonlinear viscous dampers for the seismic protection of structural systems. Bull. Earthq. Eng. 16, 963–982. doi: 10.1007/s10518-017-0233-4

CrossRef Full Text | Google Scholar

Artale, V., Navarra, G., Ricciardello, A., and Barone, G. (2017). Exact closed-form fractional spectral moments for linear fractional oscillators excited by a white noise. ASCE-ASME J. Risk Uncertain. Eng. Syst. B Mech. Eng. 3:030901. doi: 10.1115/1.4036700

CrossRef Full Text | Google Scholar

Atalik, T. S., and Utku, S. (1976). Stochastic linearization of multi-degree- of-freedom nonlinear system. Earthq. Eng. Struct. Dyn. 4, 411–420. doi: 10.1002/eqe.4290040408

CrossRef Full Text | Google Scholar

Bahnasy, A., and Lavan, O. (2013). “Linear or nonlinear fluid viscous dampers? A seismic point of view,” in Proceedings of the Structures Congress (Pittsburgh, PA). doi: 10.1061/9780784412848.197

CrossRef Full Text | Google Scholar

Barone, G., Lo Iacono, F., Navarra, G., and Palmeri, A. (2015). “A novel analytical model of Power Spectral Density function coherent with earthquake Response Spectra,” in Proceedings of the 1st International Conference on Uncertainty Quantification in Computational Sciences and Engineering (UNCECOMP 2015), eds G. S. M. Papadrakakis and V. Papadopoulos (Athens: Institute of Structural Analysis and Antiseismic Research School of Civil Engineering National Technical University of Athens (NTUA) Greece), 394–406.

Google Scholar

Barone, G., Lo Iacono, F., Navarra, G., and Palmeri, A. (2019). Closed-form stochastic response of linear building structures to spectrum-consistent seismic excitations. Soil Dyn. Earthq. Eng. 125:105724. doi: 10.1016/j.soildyn.2019.105724

CrossRef Full Text | Google Scholar

Byrd, R. H., Gilbert, J. C., and Nocedal, J. (2000). A trust region method based on interior point techniques for nonlinear programming. Math. Programming 89, 149–185. doi: 10.1007/PL00011391

CrossRef Full Text | Google Scholar

Cacciola, P., Colajanni, P., and Muscolino, G. (2004). Combination of modal responses consistent with seismic input representation. J. Struct. Eng. 130, 47–55. doi: 10.1061/(ASCE)0733-9445(2004)130:1(47)

CrossRef Full Text | Google Scholar

Connor, J. J. (2003). Introduction to Structural Motion Control. Cambridge, MA: MIT-Prentice Hall Series on Civil, Environmental, and Systems Engineering.

Google Scholar

De Domenico, D., and Ricciardi, G. (2018). Improved stochastic linearization technique for structures with nonlinear viscous dampers. Soil Dyn. Earthq. Eng. 113, 415–419. doi: 10.1016/j.soildyn.2018.06.015

CrossRef Full Text | Google Scholar

De Domenico, D., and Ricciardi, G. (2019). Earthquake protection of structures with nonlinear viscous dampers optimized through an energy-based stochastic approach. Eng. Struct. 179, 523–539. doi: 10.1016/j.engstruct.2018.09.076

CrossRef Full Text | Google Scholar

De Domenico, D., Ricciardi, G., and Takewaki, I. (2019). Design strategies of viscous dampers for seismic protection of building structures: a review. Soil Dyn. Earthq. Eng. 118, 144–165. doi: 10.1016/j.soildyn.2018.12.024

CrossRef Full Text | Google Scholar

Der Kiureghian, A. (1980). Structural response to stationary excitation. J. Eng. Mech. Div. 106, 1195–1213.

Google Scholar

Der Kiureghian, A., and Fujimura, K. (2009). Nonlinear stochastic dynamic analysis for performance-based earthquake engineering. Earthq. Eng. Struct. Dyn. 38, 719–738. doi: 10.1002/eqe.899

CrossRef Full Text | Google Scholar

Di Matteo, A., Lo Iacono, F., Navarra, G., and Pirrotta, A. (2014a). “A novel mathematical model for TLCD: theoretical and experimental investigations,” in Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management - Proceedings of the 2nd International Conference on Vulnerability and Risk Analysis and Management, ICVRAM 2014 and the 6th International Symposium on Uncertainty Modeling (Liverpool, UK).

Google Scholar

Di Matteo, A., Lo Iacono, F., Navarra, G., and Pirrotta, A. (2014b). Experimental validation of a direct pre-design formula for tlcd. Eng. Struct. 75, 528–538. doi: 10.1016/j.engstruct.2014.05.045

CrossRef Full Text | Google Scholar

Di Matteo, A., Lo Iacono, F., Navarra, G., and Pirrotta, A. (2015). Optimal tuning of tuned liquid column damper systems in random vibration by means of an approximate formulation. Meccanica 50, 795–808. doi: 10.1007/s11012-014-0051-6

CrossRef Full Text | Google Scholar

Di Paola, M., La Mendola, L., and Navarra, G. (2007). Stochastic seismic analysis of structures with nonlinear viscous dampers. J. Struct. Eng. 133, 1475–1478. doi: 10.1061/(ASCE)0733-9445(2007)133:10(1475)

CrossRef Full Text | Google Scholar

Di Paola, M., and Muscolino, G. (1988). Analytic evaluation of spectral moments. J. Sound Vibrat. 124, 479–488. doi: 10.1016/S0022-460X(88)81389-0

CrossRef Full Text | Google Scholar

Di Paola, M., and Navarra, G. (2009). Stochastic seismic analysis of MDOF structures with nonlinear viscous dampers. Struct. Control Health Monit. 16, 303–318. doi: 10.1002/stc.254

CrossRef Full Text | Google Scholar

Elishakoff, I. (2000). Stochastic linearization technique: a new interpretation and a selective review. Shock Vibr. Dig. 32, 179–188. doi: 10.1177/058310240003200301

CrossRef Full Text | Google Scholar

Fujimura, K., and Der Kiureghian, A. (2007). Tail-equivalent linearization method for nonlinear random vibration. Probabilist. Eng. Mech. 22, 63–76. doi: 10.1016/j.probengmech.2006.08.001

CrossRef Full Text | Google Scholar

Giaralis, A., and Spanos, P. D. (2010). Effective linear damping and stiffness coefficients of nonlinear systems for design spectrum based analysis. Soil Dyn. Earthq. Eng. 30, 798–810. doi: 10.1016/j.soildyn.2010.01.012

CrossRef Full Text | Google Scholar

Gidaris, I., and Taflanidis, A. A. (2015). Performance assessment and optimization of fluid viscous dampers through life-cycle cost criteria and comparison to alternative design approaches. Bull. Earthq. Eng. 13, 1003–1028. doi: 10.1007/s10518-014-9646-5

CrossRef Full Text | Google Scholar

Housner, G., Bergman, L., Caughey, T., Chassiakos, A., Claus, R., Masri, S., et al. (1997). Structural control: past, present, and future. J. Eng. Mech. 123, 897–971. doi: 10.1061/(ASCE)0733-9399(1997)123:9(897)

CrossRef Full Text | Google Scholar

Iervolino, I., Galasso, C., and Cosenza, E. (2010). REXEL: computer aided record selection for code-based seismic structural analysis. Bull. Earthq. Eng. 8, 339–362. doi: 10.1007/s10518-009-9146-1

CrossRef Full Text | Google Scholar

Igusa, T., Kiureghian, A. D., and Sackman, J. L. (1984). Modal decomposition method for stationary response of non-classically damped systems. Earthq. Eng. Struct. Dyn. 12, 121–136. doi: 10.1002/eqe.4290120109

CrossRef Full Text | Google Scholar

Makris, N., Constantinou, M. C., and Dargush, G. F. (1993). Analytical model of viscoelastic fluid dampers. J. Struct. Eng. 119, 3310–3325. doi: 10.1061/(ASCE)0733-9445(1993)119:11(3310)

CrossRef Full Text | Google Scholar

Melchers, R. (1999). Structural Reliability Analysis and Prediction, 2nd Edn. Chichester, UK: John Wiley & Sons Ltd.

Google Scholar

Mitseas, I. P., Kougioumtzoglou, I. A., Giaralis, A., and Beer, M. (2018). A novel stochastic linearization framework for seismic demand estimation of hysteretic MDOF systems subject to linear response spectra. Struct. Safety 72, 84–98. doi: 10.1016/j.strusafe.2017.12.008

CrossRef Full Text | Google Scholar

Navarra, G., Lo Iacono, F., and Oliva, M. (2017). “Probabilistic optimal design of passive control devices coherently with seismic codes response spectra,” in Proceedings of the 23rd Conference of the Italian Association of Theoretical and Applied Mechanics (AIMeTA 2017) (Rome).

Navarra, G., Lo Iacono, F., Oliva, M., and Cascone, D. (2019a). “Speeding up the stochastic linearisation for systems controlled by non-linear passive devices,” in Proceedings of the 24th Conference of the Italian Association of Theoretical and Applied Mechanics (AIMeTA 2019) (Rome).

Google Scholar

Navarra, G., Lo Iacono, F., Oliva, M., and Esposito, A. (2019b). “Design of a NES device via efficient stochastic linearisation,” in Proceedings of ICNAAM 2019 - 17th International Conference on Numerical Analysis and Applied Mathematics. (Rhodes).

Google Scholar

Oliva, M., Barone, G., and Navarra, G. (2017). Optimal design of nonlinear energy sinks for sdof structures subjected to white noise base excitations. Eng. Struct. 145, 135–152. doi: 10.1016/j.engstruct.2017.03.027

CrossRef Full Text | Google Scholar

Pinto, P., Giannini, R., and Franchin, P. (2007). Seismic reliability analysis of structures. Earthq. Eng. Struct. Dyn. 36, 2081–2081. doi: 10.1002/eqe.742

CrossRef Full Text | Google Scholar

Roberts, J., and Spanos, P. (1991). Random Vibration and Statistical Linearization. Chichester: John Wiley & Sons Ltd.

Google Scholar

Schwann, K., Reinsch, H., and Weber, F. (1988). “Description of the feature of viscous dampers on the goals of equivalent rheological models, presented for pipework dampers,” in Proceedings of the Pressure Vessels and Piping Conference, ASME (Pittsburgh, PA), 528–538.

Google Scholar

Spanos, P. D., and Giaralis, A. (2013). Third-order statistical linearization-based approach to derive equivalent linear properties of bilinear hysteretic systems for seismic response spectrum analysis. Struct. Safety 44, 59–69. doi: 10.1016/j.strusafe.2012.12.001

CrossRef Full Text | Google Scholar

Spanos, P. D., and Miller, S. M. (1994). Hilbert transform generalization of a classical random vibration integral. J. Appl. Mech. 61, 575–581. doi: 10.1115/1.2901498

CrossRef Full Text | Google Scholar

Spencer, B., and Nagarajaiah, S. (2003). State of the art of structural control. J. Struct. Eng. 129, 845–856. doi: 10.1061/(ASCE)0733-9445(2003)129:7(845)

CrossRef Full Text | Google Scholar

Takewaki, I. (1997). Optimal damper placement for minimum transfer functions. Earthq. Eng. Struct. Dyn. 26, 1113–1124.

Google Scholar

Trombetti, T., and Silvestri, S. (2004). Added viscous dampers in shear-type structures: the effectiveness of mass proportional damping. J. Earthq. Eng. 8, 275–313. doi: 10.1080/13632460409350490

CrossRef Full Text | Google Scholar

Tubaldi, E., Barbato, M., and Dall'Asta, A. (2016). Efficient approach for the reliability-based design of linear damping devices for seismic protection of buildings. ASCE-ASME J. Risk Uncertain. Eng. Syst. A Civil Eng. 2:C4015009. doi: 10.1061/AJRUA6.0000858

CrossRef Full Text | Google Scholar

Tubaldi, E., and Kougioumtzoglou, I. A. (2015). Nonstationary stochastic response of structural systems equipped with nonlinear viscous dampers under seismic excitation. Earthq. Eng. Struct. Dyn. 44, 121–138. doi: 10.1002/eqe.2462

CrossRef Full Text | Google Scholar

UNI ENV 1998:2005 (2005). Eurocode 8: Design of Structures for Earthquake Resistance Part 1: General Rules, Seismic Actions and Rules for Buildings. Brussels: Standard, CEN Central Secretariat.

Vanmarcke, E. H. (1972). Properties of spectral moments with applications to random vibration. J. Eng Mech. Div. 98, 425–446.

Google Scholar

Vanmarcke, E. H. (1975). On the distribution of the first-passage time for normal stationary random processes. J. Appl. Mech. 42:215. doi: 10.1115/1.3423521

CrossRef Full Text | Google Scholar

Vanmarcke, E. H. (1976a). “Chapter 8 - structural response to earthquakes,” in Seismic Risk and Engineering Decisions, volume 15 of Developments in Geotechnical Engineering, eds C. Lomnitz and E. Rosenblueth (Amsterdam: Elsevier), 287–337.

Google Scholar

Vanmarcke, E. H. (1976b). Structural Response to Earthquakes. Vol. 55. Mexico City: Elsevier Scientific Publishing Company.

Appendix

Stochastic model of the seismic action consistent with Response Spectra

The procedure for the optimal design of passive control devices into a probabilistic framework requires the modeling of the seismic ground motion as a stochastic process. Generally, international building codes define the seismic action by means of pseudo-acceleration elastic uniform hazard spectra associated with the peak response of linear single-degree-of-freedom systems having viscous damping. A general class of RS can be expressed as in the following four-branches expression:

$\begin{array}{ll}{S}_a\left(T\right)=\{\begin{array}{cc}{S}_0\left[1+\left(a-1\right)\frac{T}{T_3}\right]& 0\le T\le T_3\\ a{S}_0& T_3<T\le T_2\\ a{S}_0{\left(\frac{T_2}{T}\right)}^{k_1}& T_2<T\le T_1\\ a{S}_0{\left(\frac{T_2}{T_1}\right)}^{k_1}{\left(\frac{T_1}{T}\right)}^{k_2}& T>T_1\end{array}& (\mathrm{A1})\end{array}$

where T is the natural period of the SDOF system, S₀ is the peak ground acceleration, a is the dynamic amplification factor, T₁, T₂ and T₃ are the periods that define the various branches, and k₁ and k₂ are shape factors. In this paper we refer only to RS with k₁ = 1 and k₂ = 2 and in Figure A1A a qualitative representation of RS is depicted.

FIGURE A1

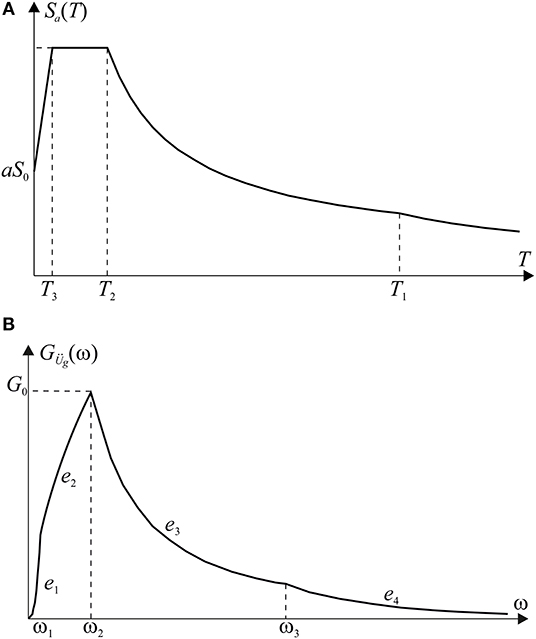
Figure A1. (A) Pseudo-acceleration Response Spectrum; (B) Power Spectral Density function coherent with Response Spectrum.

Several building codes allow for an alternative representation of the seismic ground motion by means of artificial accelerograms of nominal duration T_s that can be generated as samples of a zero-mean Gaussian stationary process, fully characterized by its one-sided PSD function G_Üg(ω).

In this work, the RS-consistent PSD was intended as an alternative conventional way to define the seismic action or, in other word, as a mathematical tool to conveniently represent the seismic action and to be used into the linear stochastic dynamic context. With this in mind, the RS-consistent PSD function is determined by solving an inverse stochastic dynamic problem in order to produces the same effects of the target RS, hence in Equation (A2) a value of ζ = 0.05 has been used. Once the PSD function was determined, it completely defines the input process from a probabilistic point of view, irrespective of the characteristics of the superimposed structure (linearity, damping values and so on). It is remarked that in some recent SL approaches (Mitseas et al., 2018) the PSD is updated at each iteration to be consistent with a RS in which damping modification factors are applied.

Seismic codes do not define the process, but require, instead, that it has to be compatible with an assigned RS, by providing the compatibility conditions. For instance, following the provision of Eurocode 8 (UNI ENV 1998:2005, 2005), a ground acceleration PSD function G_Üg(ω) is considered compatible with an assigned acceleration RS, S_a(T), if a SDOF system with an assigned damping ratio (usually ζ₀ = 0.05), subjected to accelerogram samples generated from G_Üg(ω), experiences into a time window of the nominal duration T_s of the earthquake an average absolute peak acceleration larger than 90% of S_a(T) for each value of the natural period T. If the ground motion PSD was known, the corresponding RS could be easily obtained by stochastic analysis. However, the inverse problem (i.e. determining the PSD function corresponding to an assigned RS) is not easy to solve. An approximate recursive solution for this problem has been provided in (Cacciola et al., 2004) in order to obtain an estimate of the PSD function G_Üg(ω) compatible with the assigned RS:

$\begin{array}{ll}{G}_{{\ddot{\text{U}}}_g}(\omega )=\frac{\gamma }{\omega }\left[{\left(\frac{S_a(\omega ,\zeta )}{{\eta }_U(\omega ,\zeta )}\right)}^2-{\displaystyle {\int }_0^{\omega }}{G}_{{\ddot{\text{U}}}_g}(\widehat{\omega })d\widehat{\omega }\right]& (\mathrm{A2})\end{array}$

where the parameter γ = 4ζ/(π − 4ζ) and the peak factor η_U(ω, ζ) is computed for 50% probability of non-exceedance. In this choice, a further little approximation is introduced, i.e. by confusing the mean value with the median.

Recently, an analytical model of PSD function, compatible with RS building code defined by Equation (A1), has been proposed (Barone et al., 2015, 2019) as:

$\begin{array}{ll}{G}_{{\ddot{U}}_g}\left(\omega \right)=G_0\{\begin{array}{ll}{\left(\frac{{\omega }_1}{{\omega }_2}\right)}^{e_2}{\left(\frac{\omega }{{\omega }_1}\right)}^{e_1}\hfill & 0\le \omega \le {\omega }_1\hfill \\ {\left(\frac{\omega }{{\omega }_2}\right)}^{e_2}\hfill & {\omega }_1<\omega \le {\omega }_2\hfill \\ {\left(\frac{\omega }{{\omega }_2}\right)}^{e_3}\hfill & {\omega }_2<\omega \le {\omega }_3\hfill \\ {\left(\frac{{\omega }_3}{{\omega }_2}\right)}^{e_3}{\left(\frac{\omega }{{\omega }_3}\right)}^{e_4}\hfill & \omega >{\omega }_3\hfill \end{array}& (\mathrm{A3})\end{array}$

where ω_i = 2π/T_i (i = 1, 2, 3) is the circular frequencies corresponding to the periods T_i (i = 1, 2, 3) and G₀ represents the peak value of the PSD function that occurs at the frequency ω = ω₂. The proposed model, whose graphical representation is reported in Figure A1B, depends on only five parameters, namely G₀ and the four exponents e₁, …, e₄.

In Barone et al. (2019), the procedure to determine closed-form expressions for all the parameters, starting from those of the assigned RS, is extensively reported, whereas herein only the final expressions are recalled for the sake of brevity.

$\begin{array}{l}{e}_1=2k_2-1-L\left({\omega }_1\right)\hfill \\ e_2=2k_1-1-L\left({\omega }_2\right)\hfill \\ e_3=-1-\gamma -{\beta }_{2}L\left({\omega }_2\right)\hfill \\ e_4=-1-\gamma -{\beta }_3\left(L\left({\omega }_3\right)+2\frac{a-1}{a}\right)\hfill \\ G_0=\frac{\gamma }{{\beta }_2{\omega }_2}{\left(\frac{a{S}_0}{{\eta }_U^2\left({\omega }_2\right)}\right)}^2\hfill & (\mathrm{A4})\end{array}$

in which the following positions have been made:

$\begin{array}{l}L\left(\omega \right)=2\omega \frac{d\left(\log \left({\eta }_U\left(\omega \right)\right)\right)}{d\omega }\hfill \\ {\beta }_2={\left(\frac{{\omega }_1}{{\omega }_2}\right)}^{e_2+1}\frac{\gamma +e_1+1}{e_1+1}+\left(1-{\left(\frac{{\omega }_1}{{\omega }_2}\right)}^{e_2+1}\right)\frac{\gamma +e_2+1}{e_2+1}\hfill \\ {\beta }_3={\left(\frac{{\omega }_2}{{\omega }_3}\right)}^{e_3+1}{\beta }_2+\left(1-{\left(\frac{{\omega }_2}{{\omega }_3}\right)}^{e_3+1}\right)\frac{\gamma +e_3+1}{e_3+1}\hfill & (\mathrm{A5})\end{array}$

Lastly, some seismic codes define the ground motion accelerations by means of three-branches (by setting ω₁ → 0) or two-branches RS (ω₁ → 0 and ω₃ → ∞). In these cases, the PSD analytical model is easily obtained by Equations (4) and (5), by taking into account the same positions with regards to ω₁ and ω₃.

Analytical expression for evaluating the cross-spectral moments

The proposed analytical procedure to derive the spectral moments of a set of quantity of interest Y, requires the following steps: a) execution of the generalised modal analysis; b) evaluation of the direct spectral moments of the modal oscillators; c) determination of the cross-spectral moments in the modal space; d) evaluation of the spectral moments in the geometric space. With reference to the step c), Di Paola and Muscolino (1988) demonstrated that the cross-spectral moments of any order λ_{j,Qi, Qk} may be obtained recursively as linear combinations of the direct spectral moments. In particular, real and imaginary parts of even-order cross-spectral moments can be determined as:

$\begin{array}{l}\text{Re}\left[{\lambda }_{m,Q_j,Q_k}\right]=\frac{{\left(-1\right)}^{m/2}}{2}\\ \left({\lambda }_{0,Q_j}{\gamma }_{m,k,j}{\omega }_{0j}^2+{\lambda }_{2,Qj}{\delta }_{m,k,j}+{\lambda }_{0,Q_k}{\gamma }_{m,j,k}{\omega }_{0k}^2+{\lambda }_{2,Q_k}{\delta }_{m,j,k}\right)\\ \text{Im}\left[{\lambda }_{m,Q_j,Q_k}\right]=\frac{{\left(-1\right)}^{m/2}}{2}\\ \left({\lambda }_{1,Q_j}{\epsilon }_{m,k,j}-{\lambda }_{1,Q_k}{\epsilon }_{m,j,k}+{\lambda }_{3,Q_j}{\alpha }_{m,j,k}-{\lambda }_{3,Q_k}{\alpha }_{m,k,j}\right)& (\mathrm{A6})\end{array}$

while for the odd-order cross-spectral moments:

$\begin{array}{l}\text{Re}\left[{\lambda }_{m,Q_j,Q_k}\right]=\frac{{\left(-1\right)}^{(m+1)/2}}{2}\\ \left({\lambda }_{1,Q_j}{\epsilon }_{m,k,j}+{\lambda }_{1,Q_k}{\epsilon }_{m,j,k}+{\lambda }_{3,Q_j}{\alpha }_{m,k,j}+{\lambda }_{3,Q_k}{\alpha }_{m,j,k}\right)\\ \text{Im}\left[{\lambda }_{m,Q_j,Q_k}\right]=\frac{{\left(-1\right)}^{(m-1)/2}}{2}\\ \left({\lambda }_{0,Q_j}{\gamma }_{m,k,j}{\omega }_{0j}^2+{\lambda }_{2,Q_j}{\delta }_{m,k,j}-{\lambda }_{0,Q_k}{\gamma }_{m,j,k}{\omega }_{0k}^2-{\lambda }_{2,Q_k}{\delta }_{m,j,k}\right)& (\mathrm{A7})\end{array}$

In Equations (6) and (7), the following positions have been made:

$\begin{array}{c}{\alpha }_{m,j,k}={\alpha }_{m-1,j,k}+{\omega }_{Dk}{\beta }_{m-1,j,k};\\ {\beta }_{m,j,k}=-{\zeta }_k{\omega }_{0k}{\beta }_{m-1,j,k}-{\omega }_{Dk}{\alpha }_{m-1,j,k};\\ {\gamma }_{m,j,k}={\zeta }_k{\omega }_{0k}{\alpha }_{m,j,k}+{\omega }_{Dk}{\beta }_{m,j,k};\\ {\delta }_{m,j,k}={\zeta }_k{\omega }_{0k}{\alpha }_{m,j,k}-{\omega }_{Dk}{\beta }_{m,j,k};\\ {\epsilon }_{m,j,k}=2{\zeta }_k{\omega }_k{\omega }_{Dk}{\beta }_{m,j,k}+{\alpha }_{m,j,k}\left({\omega }_{0k}^2-2{\omega }_{Dk}^2\right);& (\mathrm{A8})\end{array}$

being:

$\begin{array}{l}{\alpha }_{0,j,k}=4\left({\zeta }_j{\omega }_j+{\zeta }_k{\omega }_k\right)/K_{jk}\\ {\beta }_{0,j,k}=2\left({\omega }_{0j}^2-{\omega }_{0k}^2+2{\zeta }_j{\zeta }_k{\omega }_{0j}{\omega }_{0k}+2{\zeta }_k^2{\omega }_{0k}^2\right)/\left({\omega }_{Dk}{K}_{jk}\right)\\ K_{jk}={\left({\omega }_{0j}^2-{\omega }_{0k}^2\right)}^2+4{\zeta }_j{\zeta }_k\left({\omega }_{0j}^2+{\omega }_{0k}^2\right)\\ {\omega }_{0j}{\omega }_{0k}+4\left({\zeta }_j^2+{\zeta }_k^2\right){\omega }_{0j}^2{\omega }_{0k}^2& (\mathrm{A9})\end{array}$