Semi-actively Implemented Non-linear Damping for Building Isolation Under Seismic Loadings

It is well-known that semi-active solution can achieve building isolation with much less energy requirements than active solutions. Also, it has been shown in previous studies that compared to linear damping, non-linear damping performs better for building isolation under sinusoidal ground motions. The present study is concerned with the extension of the application of the semi-actively implemented non-linear damping to building isolation under seismic loadings. A two-degree-of-freedom (2-DOF) scaled building model is used for simulation studies. Experimental tests on a physical building model have been used to validate the effectiveness of the 2-DOF scaled building model in representing the behaviors of a physical building structure. The optimal design of the semi-actively implemented non-linear damping for building isolation under design seismic motions is then carried out using the 2-DOF scaled building model based on simulation studies. The results show that an optimal design of semi-actively implemented non-linear damping can improve the performance of building isolation under design seismic motions in terms of both absolute acceleration and inter-story drift.

Introduction

Building isolation systems are important for protecting buildings during earthquakes (Fujita et al., 2016; Hayashi et al., 2018). Traditional building isolation systems are designed using low horizontal-stiffness bearings to achieve low resonant frequencies so as to isolate earthquake loadings over a wide range of frequencies (Naeim, 1989). However, during some recent earthquakes, e.g., the 2011 Tohoku earthquake in Japan, long period ground motion with low frequencies were recorded, which was close to the resonance frequencies of some high-rise and base-isolated buildings (Takewaki et al., 2011; Kasai et al., 2013), indicating that traditional solutions may not provide desired isolation performance in these cases. Although some traditional isolation devices such as tuned mass damper (TMD) (Taniguchi et al., 2008) or enhanced variants with the inerter as tuned mass damper inerter (TMDI) (De Domenico et al., 2019) have been discussed and applied in building isolation systems, expensive costs, and sensitive adjustment to the dynamic property are required in these devices of a constructed building (Dan and Kohiyama, 2013).

The vibration around the resonant frequencies can be reduced by introducing a linear damping into the building isolation system, but this can be detrimental to the building isolation over non-resonance frequency ranges (Soong, 1990; Amini et al., 2015). Large supplemental damping combined with seismic isolation is detrimental because it increases the higher-mode response, thus having a negative effect on the superstructure acceleration and inter story drift (Kelly, 1999; De Domenico and Ricciardi, 2018). To resolve this issue, many active control techniques including the actively implemented Linear–quadratic– Gaussian (LQG) control (Liu and Wu, 2013; Wang and Dyke, 2013) have been applied to improve the building isolation performance. However, the active control techniques require large power supply and high maintenance cost (Sims et al., 1999), and the stability of the actively controlled building isolation system would also be a concern (Taniguchi et al., 2016). Recently, it has been shown that these problems can be circumvented by using a non-linear damping based isolator that can reduce transmitted vibrations over both resonant and non-resonant frequencies (Peng et al., 2010, 2011; Guo et al., 2012; Lang et al., 2013). For example, Peng et al. (2010, 2011) has shown that non-linear damping can reduce the force transmissibilities over all frequency ranges of concern for both single-degree-of-freedom (SDOF) and multi-degree-of-freedom (MDOF) systems subject to sinusoidal loadings.

In practice, a non-linear damping can be realized by using, e.g., viscous fluid dampers or friction dampers, to dissipate seismic energies for building isolation (Symans et al., 2008). However, these are usually difficult to design and implement in practice to achieve a desired damping characteristic, and a semi-active solution is considered to be an ideal solution to this problem (Guyomar and Badel, 2006; Ebrahimi et al., 2008; Laalej et al., 2012; Weber, 2014; Ho et al., 2018). For example, Laalej et al. (2012) studied the use of an MR (Magneto-Rheological) damper in an isolation system to semi-actively implement the power law non-linear damping characteristics. Ebrahimi et al. (2008) investigated the implementation of non-linear vibration absorbers using the eddy current damper.

The properties of the semi-actively implemented non-linear-damping-based building isolation system have been investigated by the authors for the cases where the seismic loadings are sinusoidal (Weber, 2014). The results indicated that the non-linear damping can provide a desired isolation performance under sinusoidal loadings. However, in practice, the seismic loadings are usually complex bandwidth or random signals, where different frequencies are interacted in the isolation system. It is significant to clarify the isolation performance of semi-active control damping subject to seismic loadings before applying the device into a building system. In the present study, the work will be extended to investigate the design and semi-active implementation of non-linear damping for building isolation under seismic loadings.

The paper is organized as follows. The performance of a semi-actively implemented non-linear-damping-based building isolation system for a laboratory physical building model under sinusoidal loadings is analyzed in section The Non-linear Damping-Based Semi-active Building Isolation System. Then, in Section Design of Non-linear Damping-Based Building Isolation System Under Seismic Ground Motions, the extension of the application of the non-linear damping technique to the cases where the building model is subject to seismic ground motions is investigated. Finally, conclusions are reached in section Conclusions.

The Non-Linear Damping-Based Semi-Active Building Isolation System

A Scaled 2-DOF Building Model With a Semi-active Isolator

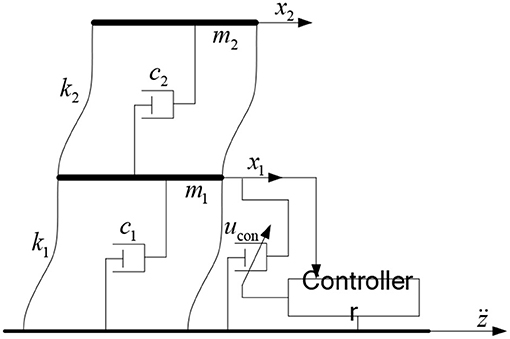
In laboratory studies, in order to investigate the performance of a building isolation system, the building system is often simplified to a mass-stiffness-damping MDOF system and then further scaled down to a 2-DOF system as shown in Figure 1 (Wang and Dyke, 2013; Amini et al., 2015; Hayashi et al., 2018; Ho et al., 2018), where the lower and upper masses represent the floor slab above the isolation layer and the superstructure of the target building, respectively. In Figure 1, m₁ and m₂ are the masses of the 2-DOF system, k₁ and k₂ are the stiffness parameters, c₁ and c₂ are damping parameters, x₁ and x₂ are the 1st and 2nd floor displacements relative to the ground motion z, respectively.

FIGURE 1

Figure 1. The scaled 2-DOF building model.

The 2-DOF building system is protected by a semi-active isolator producing a damping force determined by the ground motion acceleration $\ddot{z}$ and the first floor displacement x₁. The motion equation of the 2-DOF system with this semi-active isolator can be written as

$\begin{array}{ll}M\ddot{x}+C\dot{x}+Kx=E{u}_{\text{con}}+F\ddot{z}& (1)\end{array}$

where

$\begin{array}{l}x={\left[x_1,x_2\right]}^{\text{T}};M=\left[\begin{array}{cc}{m}_1& 0\\ 0& m_2\end{array}\right];C=\left[\begin{array}{cc}{c}_1+c_2& -c_2\\ -c_2& c_2\end{array}\right];\\ K=\left[\begin{array}{cc}{k}_1+k_2& -k_2\\ -k_2& k_2\end{array}\right];E={\left[1,0\right]}^{\text{T}};F={\left[-m_1,-m_2\right]}^{\text{T}}\end{array}$

and u_con = F_d(x₁) represents the damping force produced by the semi-active isolator, F_d(x₁) is a function dependent on x₁.

The Non-linear Damping-Based Semi-active Isolator

Consider the case where the semi-active isolator is implemented by a linear damper with three variable coefficients c_p1, c_p2 and c_p3 as shown in Figure 2. The maximum damping c_p3 is realized by closing the bottom valve and opening the top valve, the middle damping c_p2 is obtained by closing the top valve and opening the bottom valve, and the minimum damping c_p1 is generated by opening both the bottom and top valves. In addition, the damping force from the isolator is produced such that:

$\begin{array}{ll}{u}_{\text{con}}=F_d(x_1)=-c_s(t){ẋ}_1& (2)\end{array}$

where

$\begin{array}{ll}{c}_s\left(t\right)=\{\begin{array}{cc}{c}_{p1},& \text{for }{u}_d/{\dot{x}}_1\le \left(c_{p1}+c_{p2}\right)/2\\ c_{p2},& \text{for }\left(c_{p1}+c_{p2}\right)/2<u_d/{\dot{x}}_1\le \left(c_{p2}+c_{p3}\right)/2\\ c_{p3},& \text{for }{u}_d/{\dot{x}}_1>\left(c_{p2}+c_{p3}\right)/2\end{array}& (3)\end{array}$

and u_d is the desired damping force.

FIGURE 2

Figure 2. Schematic illustration of a semi-active isolator.

Figure 3A shows the MATLAB Simulink realization of a non-linear damping-based semi-active isolator where the desired force u_d is determined as a power law damping such that $u_d=-c_{n3}{{ẋ}_1}^3$ with c_n3 being the non-linear damping coefficient. The dynamics of the semi-active isolator is modeled by the first order transfer function (Ts + 1)⁻¹ where T is the time constant of the transfer function and s is the variable in the Laplace transform. The damping force u_con is produced to achieve the objective of $u_d=-c_{n3}{{ẋ}_1}^3$ by computing the selected $c_{n3}{v}^2$ value, which are either c_p1, c_p2 or c_p3, times the velocity v. Figure 3B shows how an increase of the power law damping coefficient c_n3 from c_n3,1 to c_n3,2 to c_n3,3 can approximately be realized by a switch between c_p1, c_p2 and c_p3 to produce an approximate of different cubic damping forces u_con,1, u_con,2 and u_con,3, respectively. In practice, due to the mechanics of the semi-active damping device which is modeled by (Ts + 1)⁻¹, the changing of the damping coefficients will not be a bump like Figure 3B, and will gradually shift between different damping coefficients.

FIGURE 3

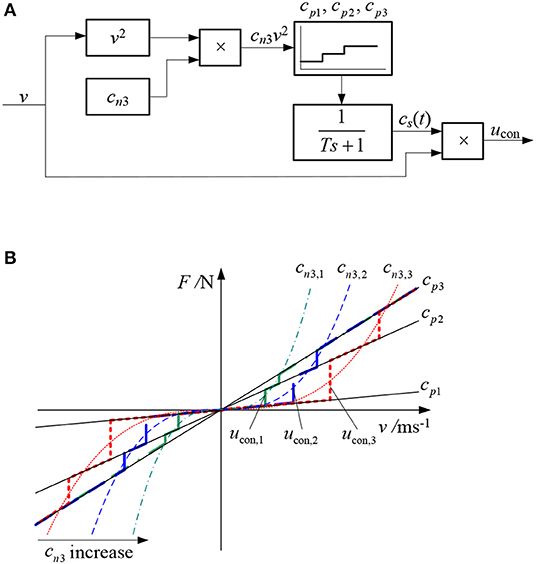
Figure 3. Semi-active implementation of non-linear damping-based isolator. (A) An illustration of the semi-actively implemented non-linear damper. (B) Semi-actively implemented damping forces under different cubic non-linear damping schemes.

Performance Under Sinusoidal Ground Motions

It has been shown in Lang et al. (2013) and Ho et al. (2018) that, under a sinusoidal ground motion given by:

$\begin{array}{ll}\ddot{z}=Asin(2\pi ft)& (4)\end{array}$

with A and f are excitation magnitude and frequency in ms⁻² and Hz, respectively, by using an appropriate non-linear damping-based semi-active isolator, the force transmissibility defined by Lang et al. (2013) and Ho et al. (2018).

$\begin{array}{ll}{T}_s(f)=\frac{\left|{F\left\{{ẍ}_i+\ddot{z}\right\}|}_{\omega =2\pi f}\right|}{A},i=1\text{ or }2& (5)\end{array}$

can be significantly reduced over both the resonant and non-resonant frequency ranges of the building system. In (5), F{.} denotes the Fourier transform operation.

For example, the parameters of a 2-DOF building model obtained by scaling down the 10-story Sosokan building model at Keio University in Japan are:

$\begin{array}{l}{m}_1=3.672\text{ kg},m_2=1.696\text{ Kg;}\\ k_1=1036\text{ N}/\text{m},k_2=5868.7\text{ N}/\text{m};\\ c_1=0.0856\text{ Ns}/\text{m},c_2=0.5367\text{ Ns}/\text{m};& (6)\end{array}$

Consider the case where the three coefficients of the linear damper that implements the semi-active isolator are designed as:

$\begin{array}{ll}{c}_{p1}=4.76\text{ Ns}/\text{m};c_{p2}=39.8\text{ Ns}/\text{m};c_{p3}=55.9\text{ Ns}/\text{m}& (7)\end{array}$

and the time constant with the damper is T = 0.155s (Nakamichi, 2018).

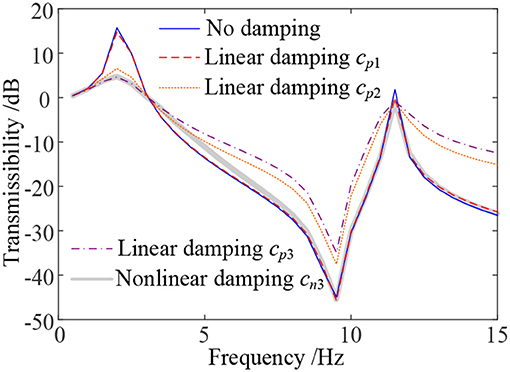
The transmissibility (5) on the first floor of the 2-DOF building model under sinusoidal input (4) with A = 1 ms⁻² and f ∈ (0, 15] Hz is shown in Figure 4, indicating the isolation performance under the non-linear damping-based semi-active isolator with $c_{n3}=3\times {10}^4\text{N}{\text{s}}^3/{\text{m}}^3$ and the performance under three linear damping-based semi-active isolators with c_s(t) = c_p1, c_p2 and c_p3, respectively.

FIGURE 4

Figure 4. Force transmissibility under linear and non-linear damping-based semi-active isolators.

From Figure 4, the advantage of non-linear damping over linear damping when the building system is subject to harmonic loadings can clearly be observed. These phenomena have been investigated in the previous studies (Lang et al., 2013) but there is still no result on the performance of the non-linear damping-based semi-active building isolation system when the system is subject to seismic ground motions.

In the following, the design and evaluation of the non-linear damping-based semi-active building isolation system will be extended to the case of a 2-DOF laboratory building model subject to seismic ground motion loadings.

Design of Non-Linear Damping-Based Building Isolation System Under Seismic Ground Motions

Comparison of the Output Response of the 2-DOF System and the Response of a Laboratory Physical Building Model to Seismic Ground Motions

Generally speaking, the seismic ground motions are random signals that contain a wide band of frequencies.

In this study, two different seismic waves including the hard-soil-layer (Type 1) and soft-soil-layer (Type 2) ground motions are considered. The time histories of the two ground motions that can be recorded in practice are produced according to different design response spectra shown in Figure 5A, where the waves were scaled down in the experiment by the scaling factor λ_t = 1/5 to the sampling time and λ_m = 5 to the magnitude as shown in Figure 5B.

FIGURE 5

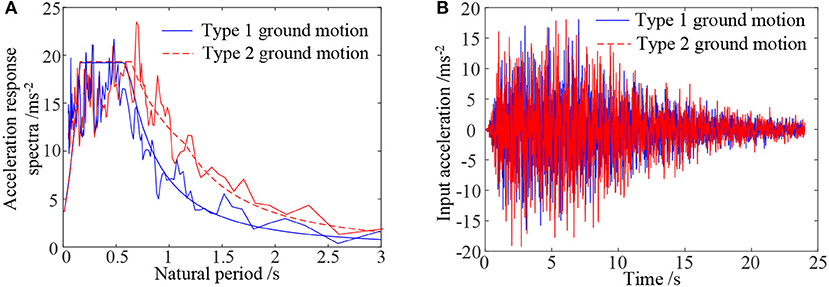
Figure 5. The response spectra and corresponding time histories of seismic ground motions. (A) The response spectra of ground motions. (B) Scaled seismic ground motions.

A 2-DOF building model test rig is shown in Figure 6, where the first floor velocity ẋ₁ is used to control the semi-active isolator with ẋ₁ estimated by a Kalman filter using the measured acceleration data $\ddot{z},{ẍ}_1$ and ẍ₂ (Dan et al., 2015; Nakamichi, 2018; Kohiyama et al., 2019). The parameters of the physical building model and the semi-active isolator are given in Equations (6) and (7), respectively. Therefore, the test rig is a 2-DOF scaled down physical model of the Sosokan building.

FIGURE 6

Figure 6. The 2-DOF scaled down laboratory physical model of the Sosokan Building.

The semi-active control damper is shown in Figure 7A, where the structure of internal electromagnetic valve is demonstrated in Figure 7B (Nakamichi, 2018). The linear damping coefficient c_p1 is achieved when two valves open, c_p2 is achieved when one valves open, and c_p3 is achieved when all valves close. Specifications of the damper and controller are listed in Table 1.

FIGURE 7

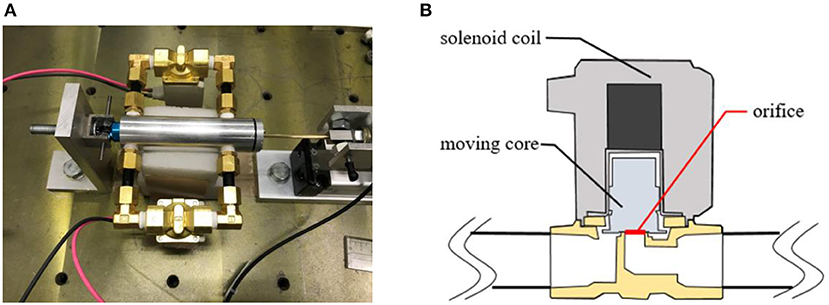
Figure 7. The semi-active control damper. (A) The damper structure. (B) The internal electromagnetic valve.

TABLE 1

Table 1. The specification of the semi-active control damper.

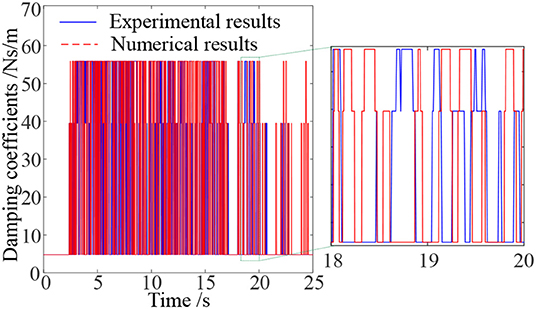
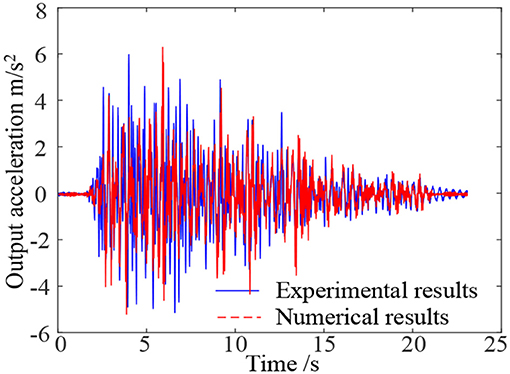
Figure 8 shows the switch-overs between the three different damping coefficients during the model simulation and experimental test on the 2-DOF scaled down building model, respectively. Both the model simulation and experimental test are undertaken under Type 1 ground motion in Figure 5A with the coefficient of non-linear damping to be implemented chosen as $c_{n3}=3\times {10}^4\text{N}{\text{s}}^3/{\text{m}}^3$. Figure 8 shows the comparison of the simulated and experimentally obtained building acceleration responses on the first floor.

FIGURE 8

Figure 8. Switch-overs of damping coefficients with semi-active isolator.

It can be seen from Figures 8, 9 that the simulation results are basically consistent with experimental ones, indicating that the 2-DOF system (6) and (7) can well represent the laboratory physical building model for the analysis and design of a semi-active building isolation system.

FIGURE 9

Figure 9. Acceleration responses.

System Analysis and Design

Consider the 2-DOF scaled down building model with parameters given by Equation (6) and the semi-active isolator with three switchable damping parameters given by Equation (7). The responses of the building model to the two seismic ground motions in Figure 5B are obtained by simulation studies. Figure 9 shows the maximum of the absolute acceleration and inter-story drift on the first and second floor, respectively. The results are obtained when Type 1 ground motion is applied and non-linear damping coefficients implemented by the semi-active isolator are varied over the range of $c_{n3}\in \left[0,10\right]\times {10}^4\text{N}{\text{s}}^3/{\text{m}}^3$. In addition, the responses of the building model under three linear damping-based isolations are also obtained and shown in Figure 9 for a comparison.

It can be seen from Figure 10 that, an increase of linear damping can reduce the maximum inter-story drift, but may increase the maximum of absolute accelerations. However, by using non-linear damping implemented by semi-active isolator, an optimal design for c_n3 can be reached such that a desired isolation performance in terms of both maximum absolute accelerations and inter story drift can be achieved.

FIGURE 10

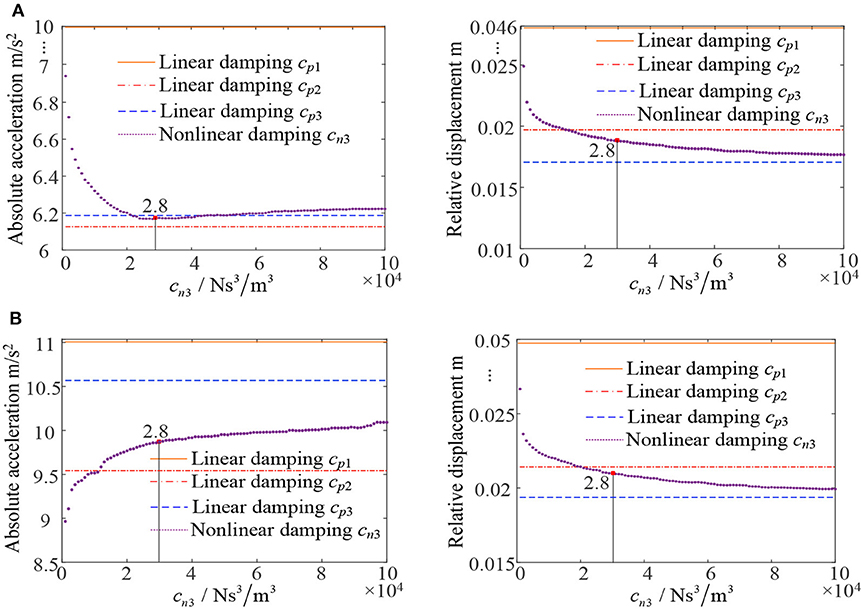
Figure 10. Maximum output acceleration and inter-story drift under Type 1 ground motion. (A) Absolute acceleration and inter-story drift of the first floor. (B) Absolute acceleration and inter-story drift of the second floor.

Figure 11 shows the same performance of the non-linear/linear damping based semi-active building isolation system but under Type 2 ground motion. Obviously, a conclusion about the optimal design of c_n3 similar to that reached from Figure 10 can be obtained.

FIGURE 11

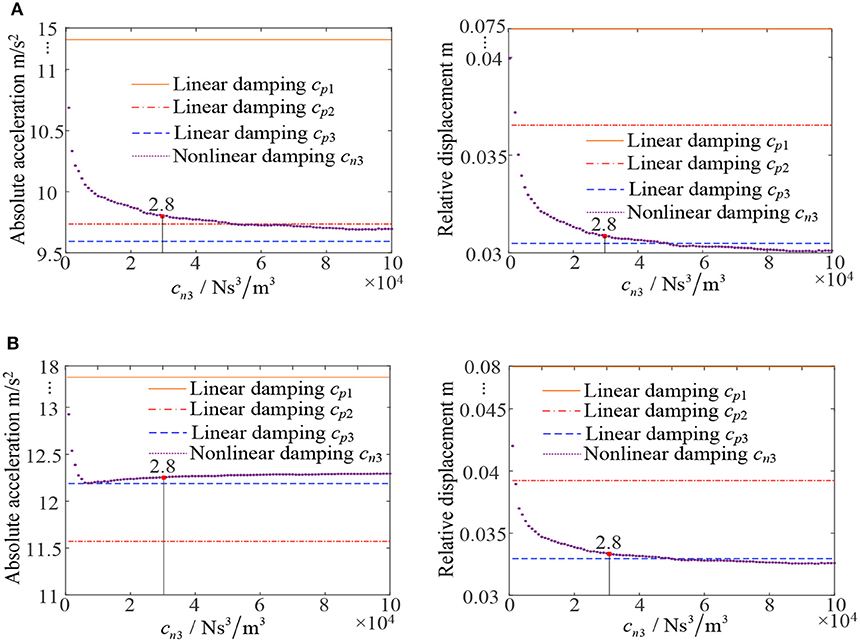
Figure 11. Maximum output acceleration and inter-story drift under Type 2 ground motion. (A) Absolute acceleration and inter-story drift of the first floor. (B) Absolute acceleration and inter-story drift of the second floor.

Based on these observations, it is possible to find a non-linear damping parameter c_n3 to achieve desired isolation performance including both the acceleration and displacement of all floors. The desired isolation performance is defined by the designer. For example, the issue of optimal design of non-linear damping parameter c_n3 can be formulated under Type 1 ground motion as follows:

Find a non-linear damping coefficient $c_{n3}={\stackrel{-}{c}}_{n3}$, such that:

$\begin{array}{ll}{\stackrel{-}{c}}_{n3}=max\left\{c_{n3}\right\}& (8)\end{array}$

subject to the constraint.

$\begin{array}{ll}\{\begin{array}{c}\max \left(\left|{\ddot{x}}_1+\ddot{z}\right|\right)\le 6.17\text{ m}/{\text{s}}^2;\max \left(\left|x_1\right|\right)\le 0.019\text{ m};\\ \max \left(\left|{\ddot{x}}_2+\ddot{z}\right|\right)\le 9.86\text{ m}/{\text{s}}^2;\max \left(\left|x_2\right|\right)\le 0.021\text{ m};\end{array}& (9)\end{array}$

The above design problem is to find the maximum value of the non-linear damping coefficient that satisfy the acceleration and displacement requirement (9). It is worth noting that the constraint (9) is only used to illustrate the design process and in practice, the optimized result may not be achieved when an inappropriate constraint is applied.

The optimal design can be numerically achieved as:

$\begin{array}{ll}{c}_{n3}=2.8\times {10}^4\text{ N}{\text{s}}^3/{\text{m}}^3& (10)\end{array}$

which is illustrated in Figures 10, 11.

It can be seen from Figures 10, 11 that, by using the optimal design (10) so as to satisfy the design requirement under Type 1 ground motion, an ideal maximum absolute acceleration and inter-story drift can also be achieved when the building system is subject to loadings represented by Type 2 ground motion.

Conclusions

The semi-active non-linear-damping-based building isolation has previously been introduced under sinusoidal ground motions to achieve low force transmissibilities over the whole frequency range of concern. However, most seismic loadings in practice are bandwidth and random signals, which are more complex than the sinusoidal loading case and there is not much researches focused on the application of semi-active damping isolation system in these scenarios before. In the present study, the base isolation under seismic ground motions and the design of the semi-active base isolation system have been studied to extend the application of the semi-active non-linear damping-based building isolation to more complicated scenarios.

A 2-DOF building model, which is a scaled down representation of the Sosokan building in Keio University in Japan, is used for the analysis and design of the semi-active non-linear damping-based building isolation system under seismic loadings. Both the acceleration and the inter-story drift of the building model have been taken into account. An optimal design of the non-linear damping parameter has been achieved numerically.

The present study shows that a desired building isolation performance under seismic loadings can be achieved by an optimally designed semi-actively implemented non-linear damping-based isolation system. Studies including the theoretical investigation and statistical design of a semi-active non-linear damping-based isolation system under various seismic ground motions will be conducted in future studies.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The research work was partly supported by the UK Royal Society (Grant number IE150298).

References

Amini, F., Mohajeri, S. A., and Javanbakht, M. (2015). Semi-active control of isolated and damaged structures using online damage detection. Smart Mater. Struct. 24:105002. doi: 10.1088/0964-1726/24/10/105002

CrossRef Full Text | Google Scholar

Dan, M., Ishizawa, Y., Tanaka, S., Nakahara, S., Wakayama, S., and Kohiyama, M. (2015). Vibration characteristics change of a base-isolated building with semi-active dampers before, during, and after the 2011 Great East Japan earthquake. Earthq. Struct. 8, 889–913. doi: 10.12989/eas.2015.8.4.889

CrossRef Full Text | Google Scholar

Dan, M., and Kohiyama, M. (2013). “Simultaneous optimization of structural shape and control system of large-scale space frame,” in 9th World Conference on Earthquake Resistant Engineering Structures, ERES 2013, A Coruña, 169–178. doi: 10.2495/ERES130141

CrossRef Full Text | Google Scholar

De Domenico, D., Deastra, P., Ricciardi, G., Sims, N. D., and Wagg, D. J. (2019). Novel fluid inerter based tuned mass dampers for optimised structural control of base-isolated buildings. J. Franklin Inst. 356, 7626–7649. doi: 10.1016/j.jfranklin.2018.11.012

CrossRef Full Text | Google Scholar

De Domenico, D., and Ricciardi, G. (2018). An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq. Eng. Struct. Dyn. 47, 1169–1192. doi: 10.1002/eqe.3011

CrossRef Full Text | Google Scholar

Ebrahimi, B., Khamesee, M. B., and Golnaraghi, M. F. (2008). Design and modeling of a magnetic shock absorber based on eddy current damping effect. J. Sound Vib. 315, 875–889. doi: 10.1016/j.jsv.2008.02.022

CrossRef Full Text | Google Scholar

Fujita, K., Miura, T., Tsuji, M., and Takewaki, I. (2016). Experimental study on influence of hardening of isolator in multiple isolation building. Front. Built Environ. 2:12. doi: 10.3389/fbuil.2016.00012

CrossRef Full Text | Google Scholar

Guo, P. F., Lang, Z. Q., and Peng, Z. K. (2012). Analysis and design of the force and displacement transmissibility of non-linear viscous damper based vibration isolation systems. Nonlin. Dyn. 67, 2671–2687. doi: 10.1007/s11071-011-0180-6

CrossRef Full Text | Google Scholar

Guyomar, D., and Badel, A. (2006). Non-linear semi-passive multimodal vibration damping: an efficient probabilistic approach. J. Sound Vib. 294, 249–268. doi: 10.1016/j.jsv.2005.11.010

CrossRef Full Text | Google Scholar

Hayashi, K., Fujita, K., Tsuji, M., and Takewaki, I. (2018). A simple response evaluation method for base-isolation building-connection hybrid structural system under long-period and long-duration ground motion. Front. Built Environ. 4:2. doi: 10.3389/fbuil.2018.00002

CrossRef Full Text | Google Scholar

Ho, C., Zhu, Y., Lang, Z. Q., Billings, S. A., Kohiyama, M., and Wakayama, S. (2018). Non-linear damping based semi-active building isolation system. J. Sound Vib. 424, 302–317. doi: 10.1016/j.jsv.2018.03.023

CrossRef Full Text | Google Scholar

Kasai, K., Mita, A., Kitamura, H., Matsuda, K., Morgan, T. A., and Taylor, A. W. (2013). Performance of seismic protection technologies during the 2011 Tohoku-Oki earthquake. Earthq. Spectra 29, S265–S293. doi: 10.1193/1.4000131

CrossRef Full Text | Google Scholar

Kelly, J. M. (1999). The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 28, 3–20. doi: 10.1002/(SICI)1096-9845(199901)28:1<3::AID-EQE801>3.0.CO;2-D

CrossRef Full Text | Google Scholar

Kohiyama, M., Omura, M., Takahashi, M., Yoshida, O., and Nakatsuka, K. (2019). Update of control parameters for semi-actively controlled base-isolated building to improve seismic performance. Jap. Archit. Rev. 2, 226–237. doi: 10.1002/2475-8876.12090

CrossRef Full Text | Google Scholar

Laalej, H., Lang, Z. Q., Sapinski, B., and Martynowicz, P. (2012). MR damper based implementation of non-linear damping for a pitch plane suspension system. Smart Mater. Struct. 21:045006. doi: 10.1088/0964-1726/21/4/045006

CrossRef Full Text | Google Scholar

Lang, Z. Q., Guo, P. F., and Takewaki, I. (2013). Output frequency response function based design of additional non-linear viscousdampers for vibration control of multi-degree-of-freedom systems. J. Sound Vib. 332, 4461–4481. doi: 10.1016/j.jsv.2013.04.001

CrossRef Full Text | Google Scholar

Liu, Y. H., and Wu, W. H. (2013). Active vibration isolation using a voice coil actuator with absolute velocity feedback control. Int. J. Autom. Smart Technol. 3, 221–226. doi: 10.5875/ausmt.v3i4.215

CrossRef Full Text | Google Scholar

Naeim, F. (1989). The seismic design handbook. New York, NY: Springer Science and Business Media. doi: 10.1007/978-1-4615-9753-7

CrossRef Full Text | Google Scholar

Nakamichi, F. (2018). Control of semi-active oil damper using local sensor for reducing equipment response (master thesis). Keio University, Hiyoshi, Japan.

Peng, Z. K., Lang, Z. Q., Jing, X. J., Billings, S. A., Tomlinson, G. R., and Guo, L. Z. (2010). The transmissibility of vibration isolators with a non-linear antisymmetric damping characteristic. J. Vib. Acoust. 132:014501. doi: 10.1115/1.4000476

CrossRef Full Text | Google Scholar

Peng, Z. K., Lang, Z. Q., Zhao, L., Billings, S. A., Tomlinson, G. R., and Guo, P. F. (2011). The force transmissibility of MDOF structures with a non-linear viscous damping device. Int. J. Non-Lin Mech. 46, 1305–14. doi: 10.1016/j.ijnonlinmec.2011.06.009

CrossRef Full Text | Google Scholar

Sims, N. D., Stanway, R., Peel, D. J., Bullough, W. A., and Johnson, A. R. (1999). Controllable viscous damping: an experimental study of an electrorheological long-stroke damper under proportional feedback control. Smart Mater. Struct. 8:601. doi: 10.1088/0964-1726/8/5/311

CrossRef Full Text | Google Scholar

Soong, T. (1990). Active Structural Control: Theory and Practice, Ser. Longman Structural Engineering and Structural Mechanics Series. London, UK: Addison-Wesley London

Google Scholar

Symans, M. D., Charney, F. A., Whittaker, A. S., Constantinou, M. C., Kircher, C. A., Johnson, M. W., et al. (2008). Energy dissipation systems for seismic applications: current practice and recent developments. J. Struct. Eng. 134, 3–21. doi: 10.1061/(ASCE)0733-9445(2008)134:1(3)

CrossRef Full Text | Google Scholar

Takewaki, I., Murakami, S., Fujita, K., Yoshitomi, S., and Tsuji, M. (2011). The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 31, 1511–1528. doi: 10.1016/j.soildyn.2011.06.001

CrossRef Full Text | Google Scholar

Taniguchi, M., Fujita, K., Tsuji, M., and Takewaki, I. (2016). Hybrid control system for greater resilience using multiple isolation and building connection. Front. Built Environ. 2:26. doi: 10.3389/fbuil.2016.00026

CrossRef Full Text | Google Scholar

Taniguchi, T., Der Kiureghian, A., and Melkumyan, M. (2008). Effect of tuned mass damper on displacement demand of base-isolated structures. Eng. Struct. 30, 3478–3488. doi: 10.1016/j.engstruct.2008.05.027

CrossRef Full Text | Google Scholar

Wang, Y., and Dyke, S. (2013). Modal-based LQG for smart base isolation system design in seismic response control. Struct. Control Health Monitor. 20, 753–768. doi: 10.1002/stc.1490

CrossRef Full Text | Google Scholar

Weber, F. (2014). Semi-active vibration absorber based on real-time controlled MR damper. Mech. Syst. Signal Process. 46, 272–288. doi: 10.1016/j.ymssp.2014.01.017

CrossRef Full Text | Google Scholar