Efficient Static Analysis of Assemblies of Beam-Columns Subjected to Continuous Loadings Available as Digitized Records

Beams, beam-columns, columns, and frames, are of major importance in structural engineering, and especially buildings and infrastructures analysis and design. In some cases, these structural members are subjected to static loadings, that though are continuous with respect to the longitudinal axes, are available as digitized records. Finite element analysis of assemblies of these members may be computationally expensive when the loading is digitized densely. In order to reduce this computational effort, attention is paid to a technique originally proposed in 2008 for reduction of the computational effort in time integration analysis. In view of the convergence-based nature of this technique, in this paper, the technique is adapted to static analysis of assemblies of beam-columns subjected to digitized loadings. The good performance of the adapted technique is demonstrated from different points of view, and is compared with the performance of the technique in time integration analysis.

Introduction

Structural systems are getting larger and behave more complicatedly day by day. Accordingly, efficient analysis of structural systems is an important concern, in areas such as optimum structural design, time history analysis, and structural control. In addition, when the structural analysis is more efficient, the pre-processing and post-processing stages may become simpler and lead to easier interpretation of the results. Some different model reduction methods are reviewed in (Besselink et al., 2013). The objective of this paper is to extend the application area of a technique proposed for more efficient time integration analysis (Soroushian, 2008) by adapting the technique to static analysis of assemblies of beam-columns (the final goal of the research, including the presentation in this paper, is to put together reductions based on the above technique in time and space).

After discretization in space, the dynamic behavior of many structural systems can be expressed as the initial value problem below (Henrych, 1990; Argyris and Mlejnek, 1991; Bathe, 1996; Belytschko et al., 2000):

$\begin{array}{l}Mü+f_{\text{int}}=f(t) 0\le t\le t_{\text{end}}\hfill \\ u(t=0)=u_0\hfill \\ \dot{u}(t=0)=\dot{u}0\hfill \\ f_{\text{int}}(t=0)=f_{{\text{int}}_0}\hfill \\ Q\le \overline{O}\hfill & (1)\end{array}$

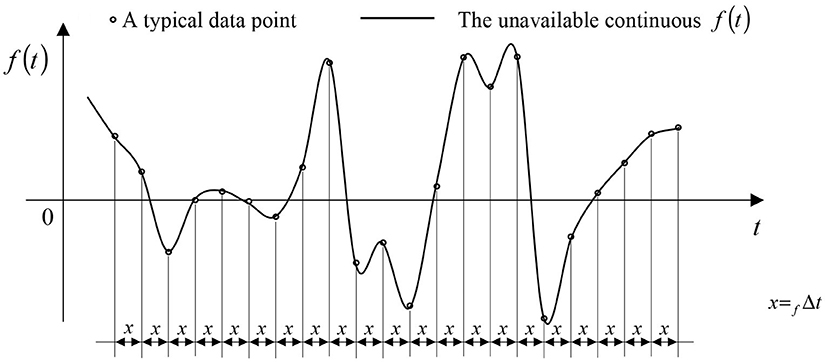
In Equation (1), M is the mass matrix, f_int stands for the vector of internal forces, f(t) implies the external force, Q represents restrictions because of non-linearity, e.g., impact and elastoplastic behavior (Hughes et al., 1979; Wriggers, 2002), t, standing for the time, is the independent variable of the initial value problem, u is the displacement vector, each top dot implies once differentiation with respect to time, “0,” as the right subscript, indicates that the argument is at its initial value, t_end is the total length of the time interval, and $\bar{\text{O}}$ stands for a zero vector or matrix. The vector f(t) might be composed of components continuous in time, but available as digitized records (see Figure 1, where _fΔt stands for the digitization step). For these cases, a technique was proposed by Soroushian (2008) to enlarge the digitization step, such that the analysis efficiency is enhanced and the analysis accuracy is practically unchanged. The technique has been implemented in analysis of different structural systems against different earthquakes by different time integration methods, considering linear and non-linear behavior, and near- and far-field earthquakes. The results evidence the good performance of the technique. Three significant applications are reviewed in Table 1 (Nateghi and Yakhchalian, 2011; Sabzei, 2013; Bastami, 2014; Garakaninezhad and Moghadas, 2015; Hadad, 2015; Soroushian et al., 2016; Zarabimanesh, 2017; Baiani, 2018; Ghondaghsaz, 2018). In view of the convergence-based mathematics of the technique (Soroushian, 2008), it seems applicable to structural systems subjected to static loadings, that are continuous with respect to the spatial coordinates, while available as digitized records. This paper is an attempt to display the validity of this idea for assemblies of beam-columns. A real example for such an application is analysis of lengthy underground structural systems. For these systems, the soil above the structural system defines a static loading that though is actually continuous with respect to the longitudinal axis, is available as a digitized record, because of the nature of the geodetic surveys; see the last example in the Numerical Study section.

FIGURE 1

Figure 1. A typical digitized component of f(t).

TABLE 1

Table 1. A brief report of the tests carried out on the technique proposed by Soroushian (2008).

In the next section, the technique proposed in Soroushian (2008) is briefly reviewed and adapted to enlargement of the beam-column elements in finite element analysis (Hughes, 1987; Bathe, 1996; Cook et al., 2002; Zienkiewicz and Taylor, 2005; Soroushian, 2008) of assemblies of beam-columns. Afterwards, via several examples, it is shown that the adapted technique might considerably reduce the analysis computational effort at the price of negligible change of accuracy. The observations are later discussed and compared with those reported from the time integration analysis application. Eventually, the paper is concluded with a brief set of the achievements and the future perspective.

From Step-Enlargement to Element-Enlargement

Convergence to exact solution is the main essentiality of successful approximate computation (Henrici, 1962; Strikwerda, 1989). In a brief review on the technique proposed by Soroushian (2008), the basis of the technique is proper convergence (Soroushian, 2010) of the computed response to the exact response. This consideration has led to the change of the f(t) digitized in _fΔt to the $\tilde{\text{f}}\mathrm{\text{(}}t\mathrm{\text{)}}$ digitized in _f Δ$\tilde{t}$ (= n _f Δt, n ∈ {2, 3, …}), according to Soroushian (2017):

$\begin{array}{l}\begin{array}{cc}{\tilde{f}}_i=\tilde{f}(t_i)& t_i=0,n_f\Delta t,2n_f\Delta t,\mathrm{...}\end{array}\hfill \\ =\{\begin{array}{cc}g(t_i)\hfill & t_i=0\hfill \\ \frac{1}{2}g(t_i)+\frac{1}{4n^{\prime }}{\displaystyle {\displaystyle \sum }_{k=1}^{n^{\prime }}}[g(t+\frac{k}{n})+g(t-\frac{k}{n})]\hfill & 0\le t_i<t^{\prime }{ }_{end}\hfill \\ g(t_i)\hfill & t_i=t^{\prime }{ }_{end}\hfill \end{array}\hfill & (2)\end{array}$

where n′can be obtained from

$\begin{array}{ll}{n}^{\prime }=\{\begin{array}{ll}n-1\hfill & \text{when }{t}_i=n_f\Delta t\hfill \\ \{\begin{array}{ccc}\frac{n}{2}& n=2j,& j\in Z^{+}\\ \frac{n-1}{2}& n=2j+1,& j\in Z^{+}\end{array}\hfill & \text{when }{t}_i\ne n_f\Delta t,t_i\ne {t^{\prime }}_{end}-n_f\Delta t\hfill \\ n-1\hfill & \text{when }{t}_i={t^{\prime }}_{end}-n_f\Delta t\hfill \end{array}& (3)\end{array}$

${t^{\prime }}_{end}$ stands for the only number satisfying the two relations below:

$\begin{array}{ll}{t}_{end}\le {t^{\prime }}_{end}<t_{end}+n_f\Delta t& (4)\end{array}$

$\begin{array}{ll}\frac{{t^{\prime }}_{end}}{n_f\Delta t}\in \left\{1,2,\dots \right\}& (5)\end{array}$

and g(t_i) is available from:

$\begin{array}{ll}g\text{(}{t}_i)=\{\begin{array}{cc}f(t_i)& \text{when }0\le t_i\le t_{end}\hfill \\ 0& \text{when }{t}_{end}\le t_i\le {t^{\prime }}_{end}\end{array}& (6)\end{array}$

From the parameters in Equation (2), n is still undefined. This parameter stands for the positive enlargement scale that should be set such that the enlargement does not affect the response accuracy. The broadly accepted comment for selection of the integration step of a time integration analysis, mainly based on accuracy considerations, is formulated as (McNamara, 1974; Clough and Penzien, 1993; Bathe, 1996; NZS 1170, 2004; Soroushian, 2017):

$\begin{array}{ll}\Delta t\le \mathrm{\text{Min}}(\Delta t_{cr},\Delta t_r,\frac{T}{\chi }{,}_f\Delta t)& (7)\end{array}$

In Equation (7), Δt_cr stands for the largest step providing numerical stability, Δt_r is the largest digitization step acceptable for the response, T is the smallest period with worthwhile contribution in the response, and χ is available from:

$\begin{array}{ll}\chi =\{\begin{array}{ll}10\hfill & \text{when the behavior is linear}\hfill \\ 100\hfill & \begin{array}{l}\text{when the behavior is nonlinear but not}\\ \text{involved in impact}\end{array}\hfill \\ 1000\hfill & \text{when the behavior is involved in impact}\hfill \end{array}& (8)\end{array}$

Consequently, the largest value that can be assigned to n, i.e., n_max, is obtainable from:

$\begin{array}{ll}\begin{array}{c}{n_{max}}_f\Delta t\le \mathrm{\text{Min}}(\Delta t_{cr},\Delta t_r,\frac{T}{\chi })<{(n_{max}+1)}_f\Delta t\\ n_{max}\in \left\{2,3,4,\dots \right\}\hfill \end{array}& (9)\end{array}$

and any positive integer larger than one and smaller than or equal to n_max can be assigned to n, i.e.,

$\begin{array}{ll}1<n\le n_{max}& (10)\end{array}$

Considering cases of the first relation in Equation (9), that lead to n_max = 0 or n_max = 1, there is no guarantee to be able to assign a value to n. In these cases, the technique proposed by Soroushian (2008) is inapplicable. In view of Table 1, this is a rare situation and the technique is successfully applicable to many real analyses. In order to extend the application to analysis of assemblies of beam-columns subjected to digitized static loadings on longitudinal axes of the beam-columns, the longitudinal axis of each beam-column is considered as the time axis and the digitized static loading is considered as the f(t) in Equations (2, 6). Considering these, the technique would be applicable when the accuracy requirements (as stated in Equation (9) for time integration) are satisfied and:

$\begin{array}{ll}{t^{\prime }}_{end}=t_{end}& (11)\end{array}$

Equation (11) is taken into account, because of the essentiality to preserve the geometry of the structural system. To satisfy this restriction, attention is paid to the fact that, if without the restriction, x_end and ${x^{\prime }}_{end}$ (defined in few lines), are sufficiently close, i.e.,

$\begin{array}{ll}0<\frac{{x^{\prime }}_{end}-x_{end}}{x_{end}}<<1,& (12)\end{array}$

we might be able to eliminate this difference by shortening the distance between each two sequential data of the static loading, i.e., _fΔx, (corresponding to _fΔt) instead of increasing the length of the beam-column. In Equation (12), ${x^{\prime }}_{end}$ and x_end are the parameters corresponding to ${t^{\prime }}_{end}$ and t_end (in application of the technique to time integration analysis, respectively). In view of Equation (4), for the validity of Equation (12) it is sufficient to guarantee

$\begin{array}{ll}\frac{{n_x}_f\Delta x}{x_{end}}<<1& (13)\end{array}$

where with attention to Equations (9, 10), n_x (the parameter corresponding to the n, defined for finite element analysis of beam-column assemblies) can be obtained from

$\begin{array}{ll}\begin{array}{c}1<n_x\le {(n_x)}_{max}\hfill \\ {{(n_x)}_{max}}_f\Delta x\le \mathrm{\text{Min}}(\text{OP},\text{AC})<{({(n_x)}_{max}+1)}_f\Delta x\hfill \\ n_x\in \left\{2,3,4,\dots \right\},{(n_x)}_{max}\in \left\{2,3,4,\dots \right\}\hfill \end{array}\hfill & (14)\end{array}$

and OP and AC are schematic representations of the restrictions on (n_x)_max, respectively originated in the response digitization and the response accuracy. Consequently, when Equation (13) is satisfied, we can redefine _fΔx as:

$\begin{array}{ll}{}_f\Delta x^{\prime }{=}_f\Delta x\frac{x_{end}}{{x^{\prime }}_{end}}& (15)\end{array}$

and consider implementation of Equation (15) as a reasonable way for preserving lengths of the beam-columns in the finite element model. A question in this stage is that under Equation (13), the change of the members lengths will be negligible even if we do not implement Equation (15). Why cannot we accept the approximation because of the replacement of x_end with ${x^{\prime }}_{end}$? In response to this question, changes of the structure's geometry can considerably change the mathematical model for the effects of geometric non-linearity (Gao and Strang, 1989; Bathe, 1996). This is true, especially when the structural members' lengths differ considerably. These changes should be avoided. Another ambiguity is on the inequality sign in Equation (13). What is the notion of the “very small”? In response to this question, it seems to the authors that because of the second order of convergence in many practical analyses, it is sufficient to satisfy

$\begin{array}{ll}\frac{{n_x}_f\Delta x}{x_{end}}<0.01& (16)\end{array}$

Furthermore, one may ask whether the above-mentioned change in the element length can be used in time integration analysis in order to avoid replacement of t_end with ${t^{\prime }}_{end}$. The response is negative. The reason is that different from static finite element analysis, time integration analysis has a step-by-step nature, where the error because of the change in the integration step can be accumulated to some level. In addition, in time integration analysis, the replacement of t_end with ${t^{\prime }}_{end}$ is not important.

Finally, it is worth noting that, even when Equations (13, 16) are not satisfied, the technique proposed by Soroushian (2008) is applicable by considering a small element in the end of the beam-column. This will not affect the accuracy and will trivially affect the computational effort. However, the pre-processing stage will become slightly more complicated. In view of the rareness of this condition, for the sake of brevity, the detailed discussion is left for future studies.

Consequently, provided we can assign positive integers larger than one to n_x, we would be able to implement the technique proposed by Soroushian (2008) in static finite element analysis of assemblies of beam-columns subjected to digitized excitation. The efficiency is studied next, and a complementary discussion on efficiency and determination of n_x is presented later.

Numerical Study

Introduction

The objective of this paper is to respond to the question: Can the technique proposed by Soroushian (2008) be successful when implemented in analysis of assemblies of beam-columns subjected to static loadings, originally continuous but available as digitized records? This section presents a numerical study on the response of this question. We examine the existence of a value of n_x causing negligible change of accuracy and sufficient reduction of computational effort, regardless of Equation (14), the resulting (_nx)max, and the possibility of assigning fractional numbers larger than one to n_x (Soroushian et al., 2017). The accuracy is studied by depicting the responses obtained from finite element analysis and the computational effort is studied in different ways.

A Simple Example

The system under consideration in this example is the beam displayed in Figure 2. IPB 500 is used as the beam profile, with a moment of inertia equal to 1.072 × 10⁵cm⁴ and a modulus of elasticity equal to 210GPa (Gaylord et al., 1997). The digitization step of the static loading equals _fΔx = 0.02m. The analysis is carried out by two-node beam-column elements (with six and twelve degrees of freedom in two- and three-dimensional analyses, respectively) loaded uniformly along the element axis. The intensity of loading on each element equals the average of the actual loadings at the element's nodes (see Figure 1). First, an analysis is carried out with elements sized equal to the loading digitization step. The displacement shear and moment diagrams are depicted in Figure 3A. The analysis is then repeated with 4 times larger elements after implementation of the technique proposed by Soroushian (2008), considering n = n_x = 4, and the results are reported in Figure 3B.

FIGURE 2

Figure 2. Structural system under consideration in the first example (A) structural model and (B) digitized static loading.

FIGURE 3

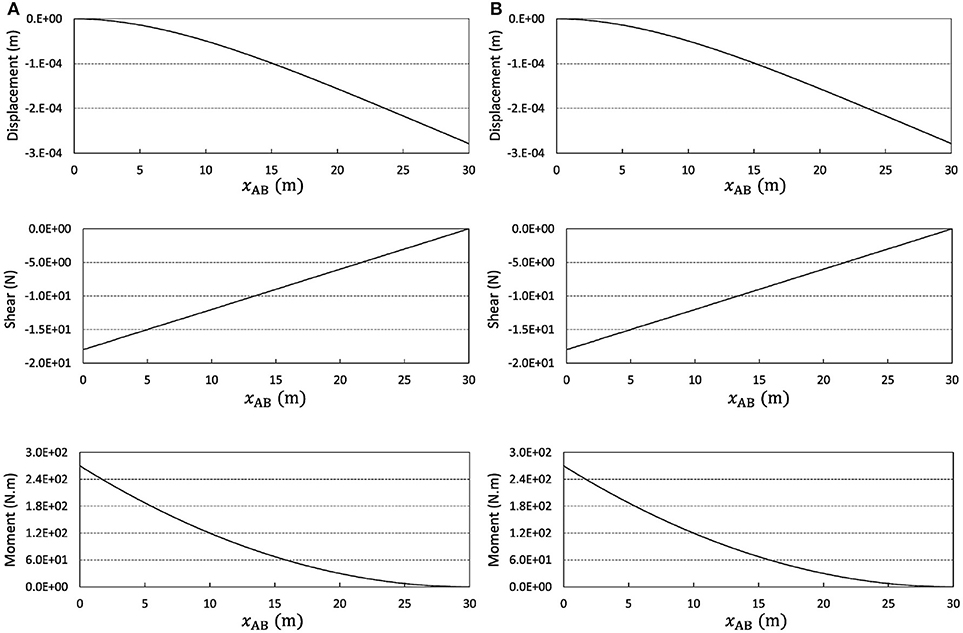
Figure 3. Responses of the structural system in the first example obtained from finite element analysis using elements sized (A) 0.02m and (B) 0.08m.

Apparently, the change of accuracy is trivial, while the reduction of the computational effort is considerable. The experience reported above clearly displays that the technique proposed for more efficient time integration analysis (Soroushian, 2008) can also be effectual in enhancement of finite element analysis.

Complicated Examples

Loading Non-perpendicular to the Member Axis in Linear/Nonlinear Analysis

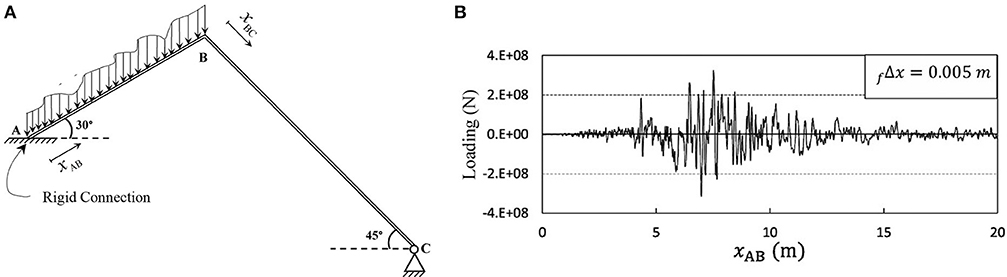
Consider the structural system introduced in Figure 4A and Table 2. The finite element analysis is carried out using elements similar to the previous example and sized _fΔx (see Figure 4B). The results are displayed in Figure 5A. The analysis is repeated with 3 times larger elements and has led to Figure 5B. The two analyses are repeated, while considering the non-linearity because of large displacements (Gao and Strang, 1989; Bathe, 1996), and the results are reported in Figure 6. In view of these results, the change of accuracy is unrecognizable, regardless of the non-linearity. The two examples in this section, and specifically Figures 5 and 6, clearly reveal the possibility to expect good performance from the technique proposed by Soroushian (2008), when implemented in finite element analysis of static linear and static non-linear behaviors of assemblies of beam-columns subjected to digitized loadings, not necessarily perpendicular to the beam-columns axes.

FIGURE 4

Figure 4. Structural system in the second example (A) structural model and (B) loading.

TABLE 2

Table 2. Properties of the structural members in Figure 4A.

FIGURE 5

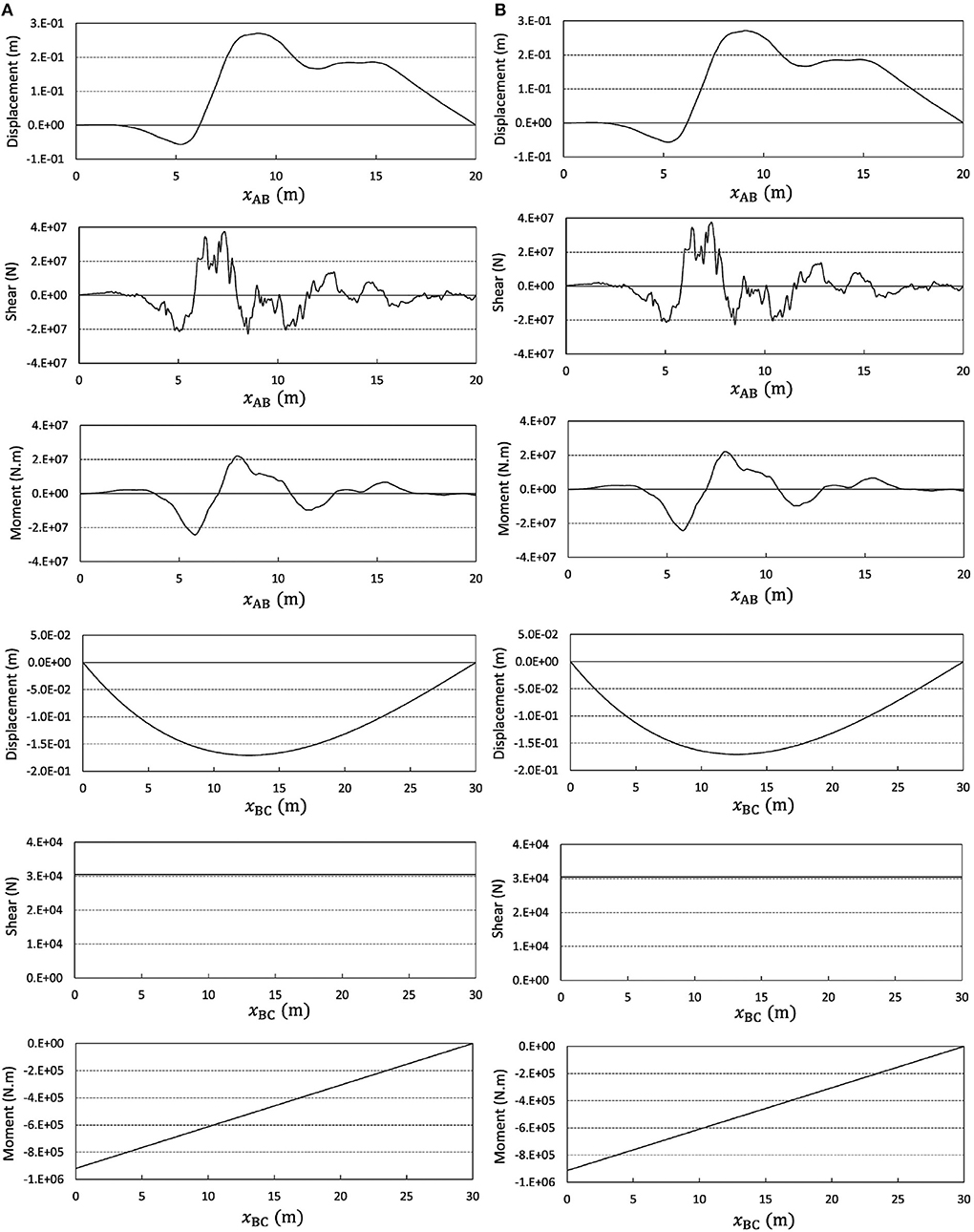
Figure 5. Responses of the second example obtained from analysis with elements sized (A) _fΔx and (B) 3_fΔx.

FIGURE 6

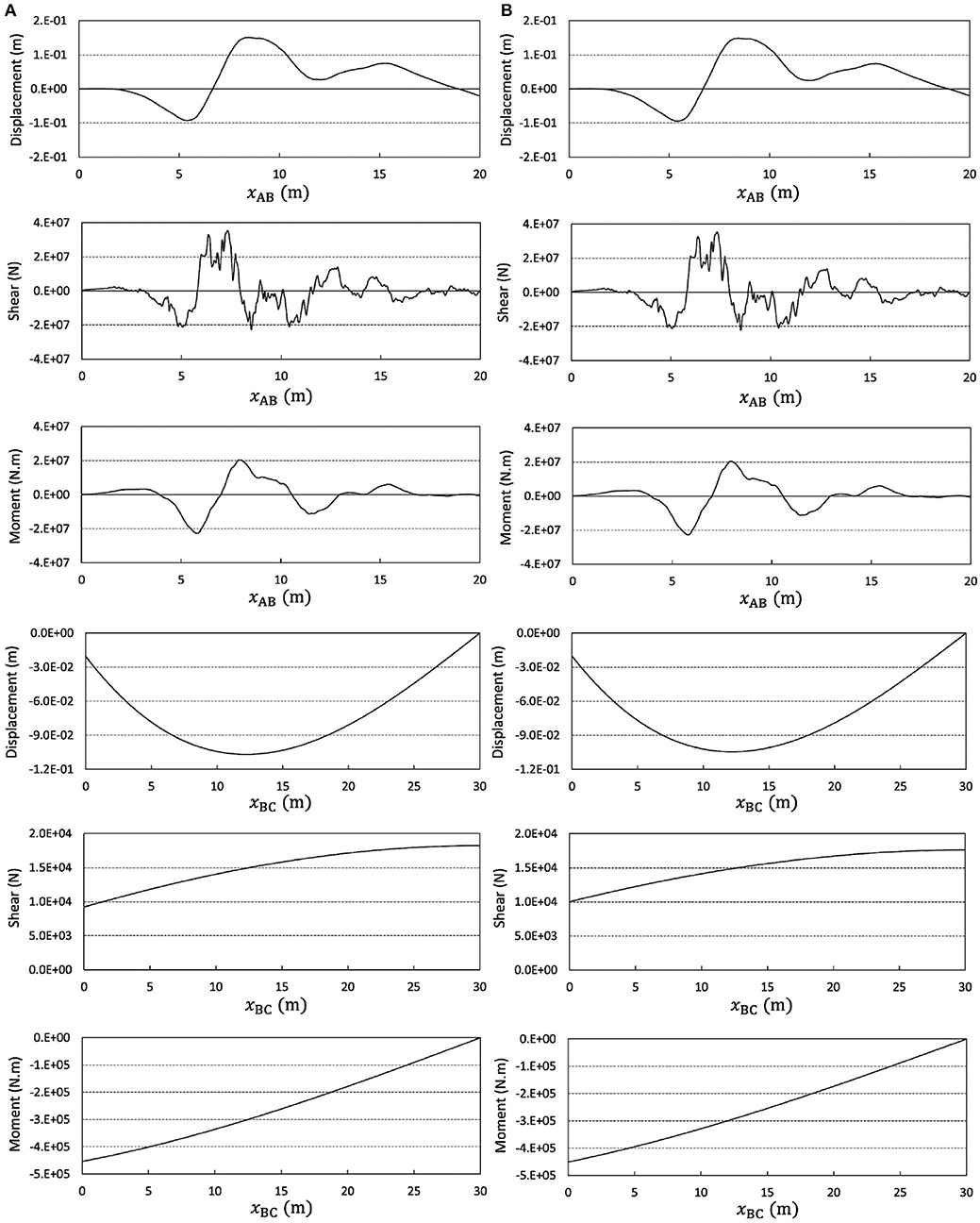
Figure 6. Responses of the second example considering large displacements and obtained from analysis with elements sized (A) _fΔx and (B) 3_fΔx.

Curved Beam-Column in Linear/Non-linear Analysis

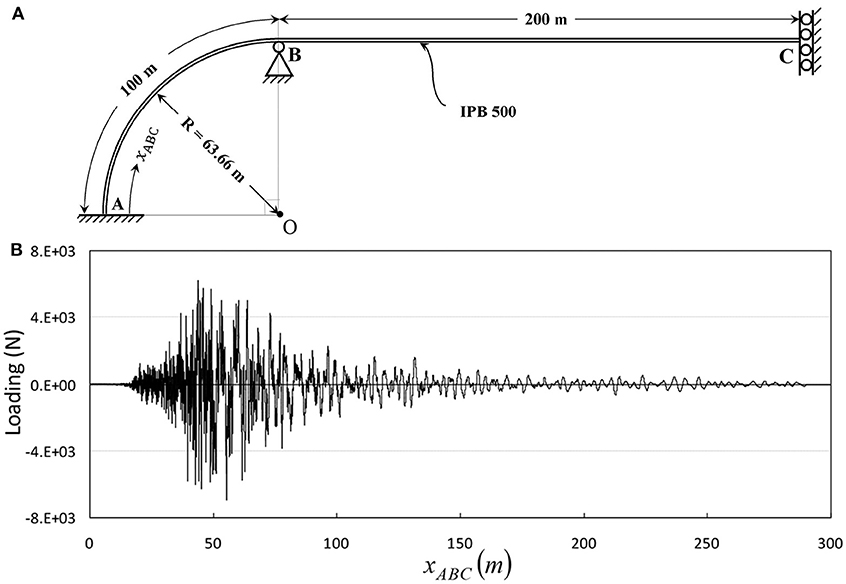
The structural system under consideration is introduced in Figure 7, where the static loading is applied in the vertical direction regardless of the position (see Figure 7B). Using the element type addressed in the previous examples has led to the responses reported in Figure 8. This is another evidence for the applicability of the technique proposed by Soroushian (2008), in analysis of assemblies of beam-columns (taking into account the modification addressed in Section From Step-Enlargement to Element-Enlargement). In view of the geometry of the structure in this example, the study is repeated considering the non-linearity because of large displacements. The consequence, reported in Figure 9, is conceptually similar to the results of the linear analysis reported in Figure 8. This implies that the technique can display a good performance in different static behaviors of beam-columns, even when the beam-columns are curved.

FIGURE 7

Figure 7. Structural system in the third example (A) structural model and (B) loading.

FIGURE 8

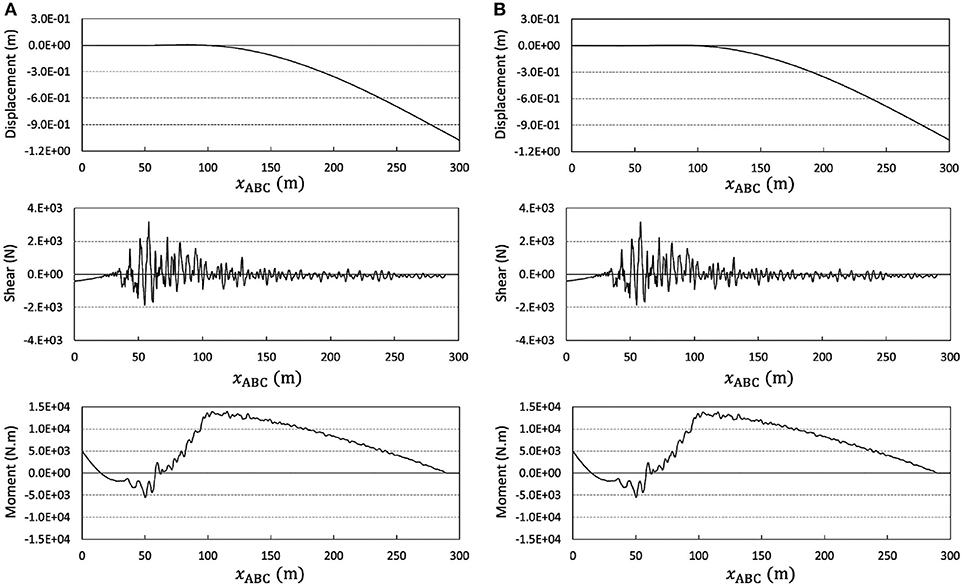
Figure 8. Responses of the third example obtained from analysis with elements sized (A) _fΔx and (B) 4_fΔx.

FIGURE 9

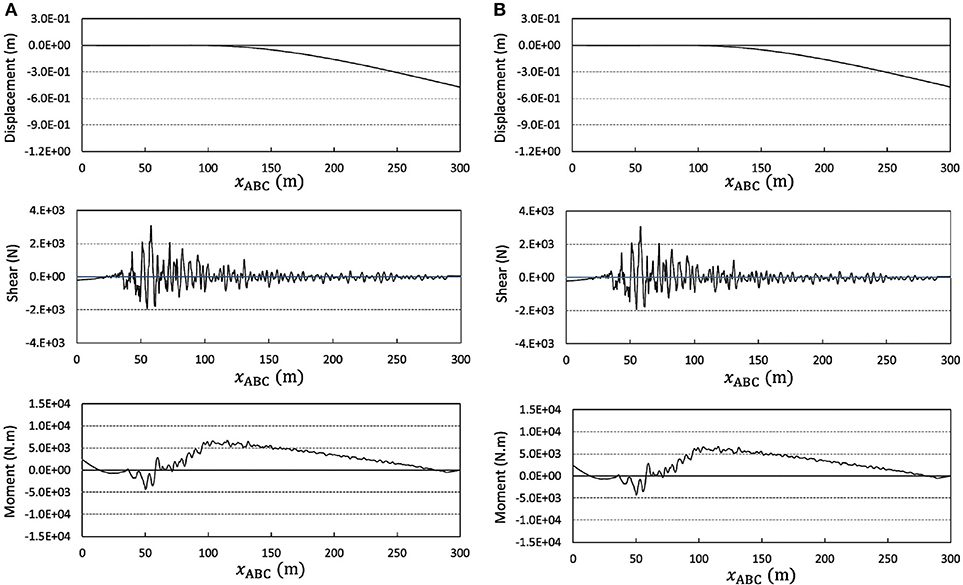
Figure 9. Responses of the third example taking into account large displacements and obtained from analysis with elements sized (A) _fΔx and (B) 4_fΔx.

A More Realistic Example

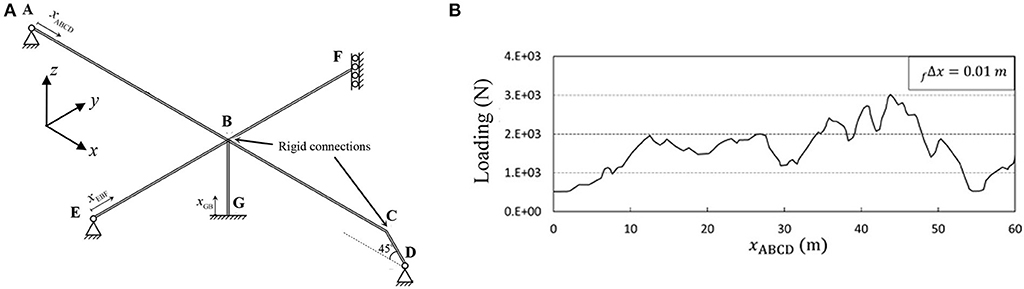
Consider the system introduced in Figure 10 and Tables 3, and 4, as a simplified model of a real structural system. Figure 10B displays a loading originated in the longitudinal profile of the Brenner Base tunnel, which is a part of the future TEN No. 5 corridor Helsinki-Valleta (Bergmeister, 2012). Via this assembly of beam-columns, and by finite element analysis with the elements in the previous examples, the performance of the technique proposed by Soroushian (2008) is tested. The consequence is reported in Figure 11, once again evidencing the good performance of the technique when applied to analysis of assemblies of beam-columns. Compared to previous examples, the contribution of lower frequencies is much more in this example (see Figure 12). This implies versatility of the technique with respect to the digitized loading. In this regard, Figures 13, and 14, display a replacement of Figures 10B, and 11, as an evidence for the versatility considering a specific assembly of beam-columns. Furthermore, comparison between Figures 11 and 14 reveals that, as implied in the AC in Equation (14), the enlargement of the element size corresponding to trivial change of accuracy can also depend on the response.

FIGURE 10

Figure 10. Structural system in the last example (A) structural model and (B) loading.

TABLE 3

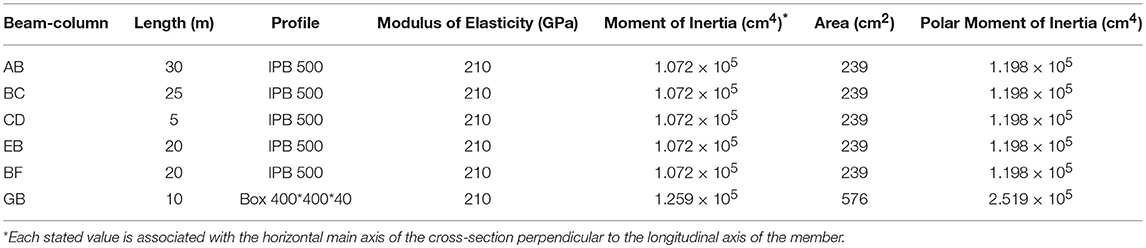
Table 3. Properties of the structural members in Figure 10A.

TABLE 4

Table 4. Complementary details of the supports of the structural system displayed in Figure 10A.

FIGURE 11

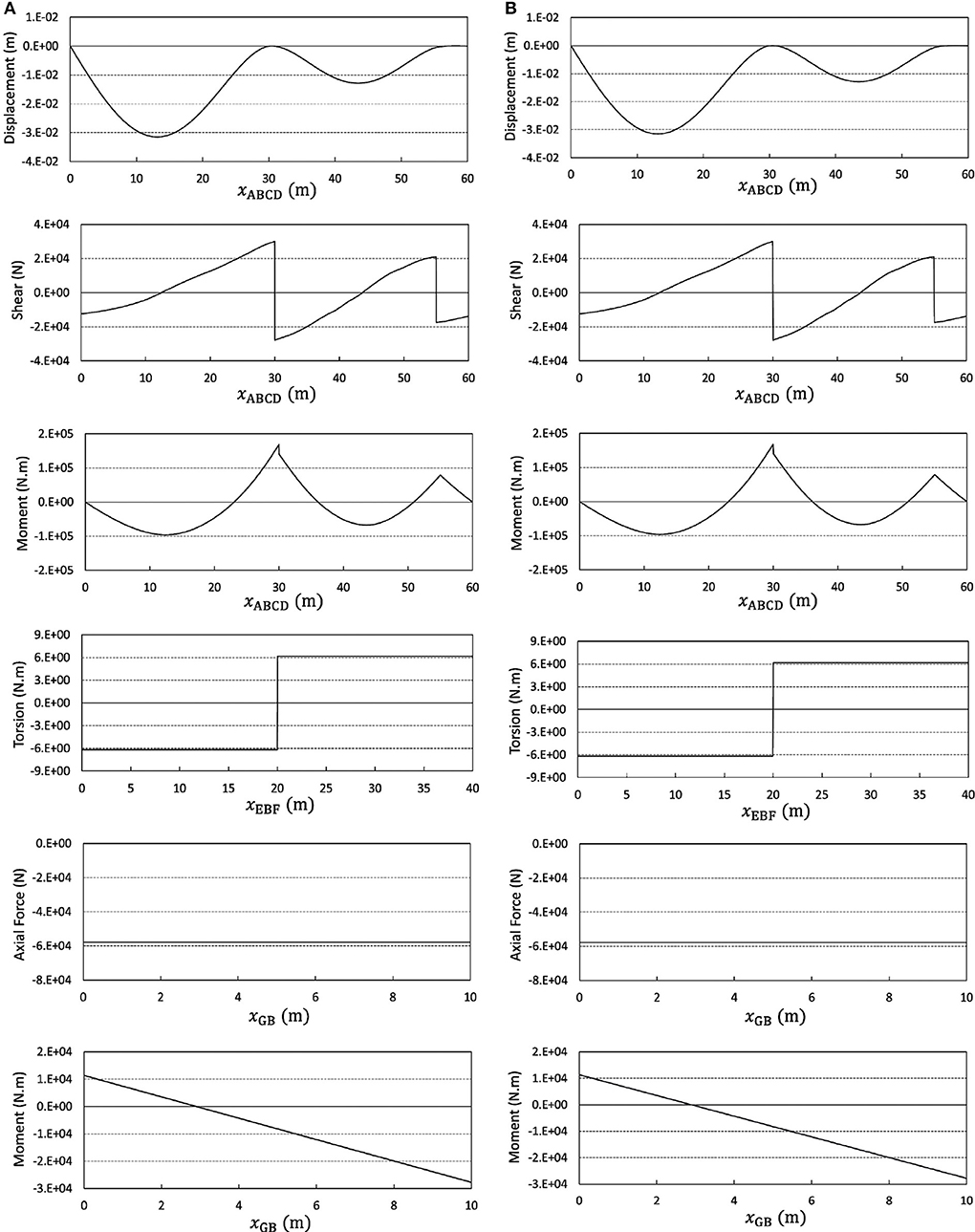
Figure 11. Responses of the fourth example obtained from finite element analysis using elements sized (A) _fΔx and (B) 4_fΔx.

FIGURE 12

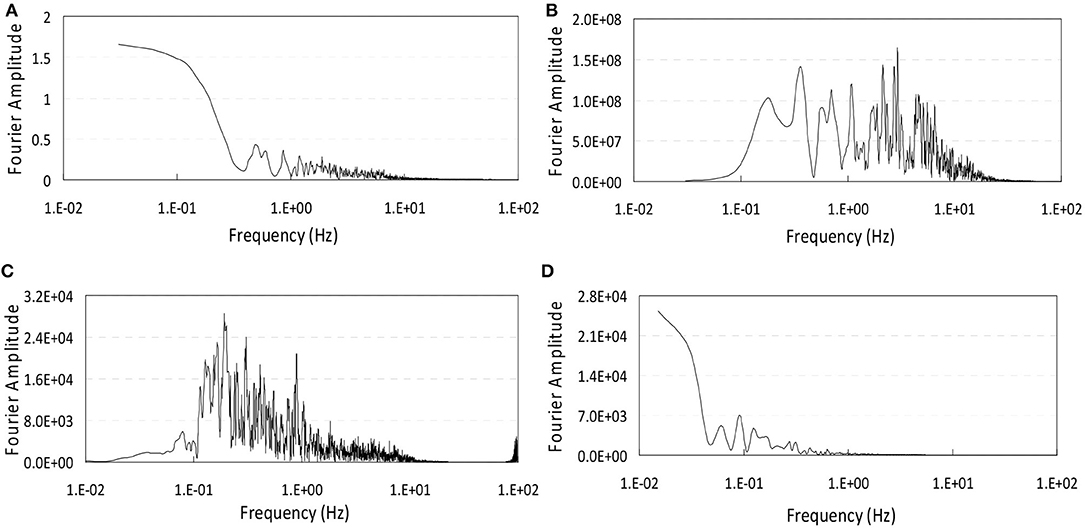
Figure 12. Frequency contents of the static loadings in the (A) first example, (B) second example, (C) third example and (D) forth example.

FIGURE 13

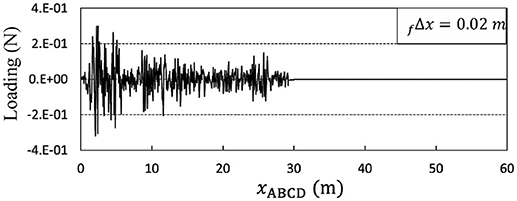
Figure 13. A replacement for Figure 10B for further study on the versatility.

FIGURE 14

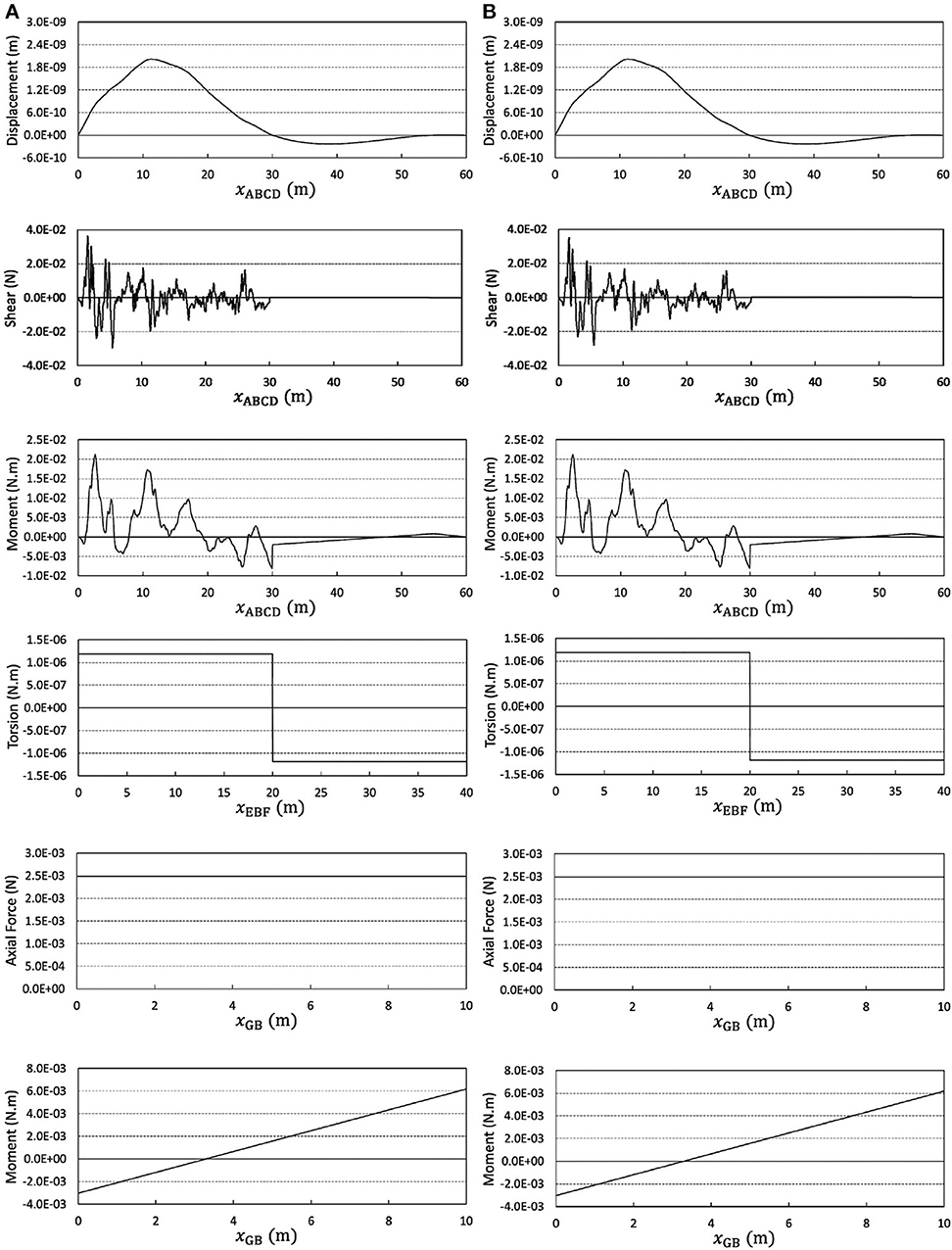
Figure 14. A consequence of the replacement addressed in Figure 13 (A) analysis with elements sized_fΔx and (B) analysis with elements sized 2_fΔx.

More on the Efficiency

According to the almost perfect accuracy observed in Sections A Simple Example, Complicated Examples, and A More Realistic Example, the efficiency can be compared in view of computational effort. Accordingly, less computational effort implies more efficiency. Computational effort can be studied in terms of the in-core storage involved in the computation (Monro, 1982; Soroushian and Farjoodi, 2003; Zhou and Tamma, 2004). With attention to the details of finite element analysis (Hughes, 1987; Bathe, 1996; Cook et al., 2002; Zienkiewicz and Taylor, 2005), the storage changes with the α th power of the number of the degrees of freedom, where 2 < α < 3 (Cook et al., 2002). Consequently, the change of efficiency, E, because of implementation of the technique proposed by Soroushian (2008) can be addressed as

$\begin{array}{ll}\frac{E_{2008}}{E_{\mathrm{\text{tr}}}}\approx n_x^{\alpha }(\frac{T{R}_{\mathrm{\text{tr}}}}{T{R}_{2008}}),2<\alpha <3& (17)\end{array}$

where TR stands for the run-time and the right subscripts “tr” and “2008”, respectively indicate the traditional (ordinary) analysis and the analysis after implementation of the technique proposed by Soroushian (2008), considering n_x as the enlargement scale (n = n_x). Equation (17), together with Figures 3, 5, 6, 8, 9, 11, and 14, and Table 5, clearly evidence the significantly increased efficiency of the analysis after implementing the above-mentioned technique, at the price of trivial change of accuracy. Furthermore, the percentage of the enhancement of efficiency, EE, can be expressed as

$\begin{array}{ll}EE=\left(\frac{E_{2008}}{E_{\mathrm{\text{tr}}}}-1\right)\times 100\%=\left(n_x^{\alpha }\frac{T{R}_{\mathrm{\text{tr}}}}{T{R}_{2008}}-1\right)\times 100& (18)\end{array}$

which, in view of Equations (14, 17) and the fact that TR_tr > TR₂₀₀₈, is at least 300%, for the presented finite element application (EE_femb ≥ 300%; the subscript “femb” stands for finite element analysis of beam-columns). The smallest EE in implementation of the technique proposed by Soroushian (2008) in time integration analysis is 100% [both when disregarding the fractional enlargement proposed by Soroushian et al. (2017)].

TABLE 5

Table 5. Values of n_x,TR_tr, and TR₂₀₀₈ in the four examples studied in Sections A Simple Example, Complicated Examples, and A More Realistic Example*.

Discussion

Static loadings addressed in Section Numerical Study vary from the slow changing loading in the last example to the rapid changing loadings in the second and third examples (the rapid case is rare). The technique proposed by Soroushian (2008) has been significantly successful in implementation in analysis of beam-column assemblies subjected to all of these loadings; see Sections A Simple Example, Complicated Examples, A More Realistic Example, and More on the Efficiency, and Equation (18). Even more, compared to time integration application, the enhancement because of the technique is considerably more in finite element analysis of beam-column assemblies; see Equation (17) and the corresponding relation in time integration application, i.e.,

$\begin{array}{ll}\frac{E_{2008}}{E_{\mathrm{\text{tr}}}}=(\frac{T{R}_{\mathrm{\text{tr}}}}{T{R}_{2008}})\approx n& (19)\end{array}$

Meanwhile, it is worth noting that, as obvious in Equations (17) and (19) and Table 5, different from time integration application, in the finite element application, the enhancement of efficiency is because of both faster analysis and less in-core storage. Considering these, further study on the extension reported in this paper is reasonable. In this regard, attention should be paid to the fact that time integration and finite element analyses are different in nature. As a main difference, while the former is a mean to analyze ordinary initial value problems, the latter is a tool for analysis of boundary value problems. Because of this difference, the invalidity of Equation (11) does not impose additional errors to time integration applications, while ${x^{\prime }}_{end}\ne x_{end}$ may lessen the accuracy of the results in finite element analysis applications. Another considerable difference is the amount of efficiency, which can lead to:

(1) Sufficiency of upper-bounding n_x by 4 [the upper-bound for time integration analysis is 5 (Azad, 2015)], i.e.,

$\begin{array}{ll}{n}_x\le 4& (20)\end{array}$

Assigning larger values to n_x enhances the efficiency trivially.

(2) Importance of fractional enlargement of digitization step (Soroushian et al., 2017), especially when Equation (14) leads to

$\begin{array}{ll}{n}_x=1& (21)\end{array}$

Therefore, further study on the extension of the technique proposed by Soroushian (2008) to static analysis of structures by finite elements is of high importance. It also sounds reasonable to expect good performance, when applying the technique to dynamic finite element analysis of different structural systems. Even more, in continuation of the extension presented in this paper, the enlargement of the digitization step (Soroushian, 2008) can be tested in other analyses, in the broad range of science and engineering computation. In addition, it is essential to note that, similar to time integration application, in implementation of the technique to finite element analysis, determination of the adequate amount of enlargement is not easy. The reason is the dependence of the AC in Equation (14) to the response.

Conclusions

The technique proposed by Soroushian (2008) has been adapted to finite element analysis of assemblies of beam-columns subjected to continuous static loadings, available as digitized records. As the main consequences,

1) The extension can be successful in linear and non-linear analyses, for different target responses, when the beam-columns are straight or curved, and the loadings are perpendicular or non-perpendicular to the axes of the beam-columns, and change gradually or sharply.

2) Implementation of the technique to static finite element analysis of structural systems may suffer from an additional source of error originated in the length of the structural members. This can be obviated by satisfying Equations (13, 16) or assigning a slightly different size to one of the elements in modeling the structural member.

3) For a specific digitization-step enlargement, enhancement of efficiency because of the technique can be considerably more in finite element analysis of beam-columns' assemblies compared to time integration analysis. A main reason is that, in the finite element analysis application, the enhancement of efficiency is via the decrease of the run-time as well as the decrease of the in-core storage. In the time integration application, only the run-time decreases.

4) The capability to enlarge the digitization step by fractional scales is very important in the finite element analysis.

5) Practically, in application of the step-enlargement technique to static finite element analysis, it is meaningless to enlarge the digitization step more than 4 times.

6) Similar to the time integration application, ambiguities exist in determination of n_x in the finite element application.

As a perspective of future, more tests on larger and more complicated assemblies of beam-columns is recommended. Further study on improvement of the existing step-enlargement technique in time integration, as well as finite element analysis, especially on clearer determination of n and n_x, is recommended. Meanwhile, extension of the step-enlargement technique to other problems and computational methods, specifically simultaneous model reduction in space and time, is a reasonable area for further research.

Author Contributions

AS conceived the main idea, and the idea of preparing the paper. The draft was prepared by the collaboration of both authors. The structural analysis of the examples and the typing of the draft was done by EF. The final editing of the manuscript was done by AS.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors sincerely appreciate the detailed comments as well as the kind attention and time of the reviewers, because of which, the quality of the paper has been enhanced significantly. The authors feel essential to also express their sincere gratitude to the editor of the paper for his managing all of the process of the paper's revision in a short time interval. Last but not the least thanks of the authors go to the typesetter(s) of the paper, who with considerable patience implemented the many changes asked by the authors.

References

Argyris, J., and Mlejnek, H. (1991). Dynamics of Structures, Volume 5 (Texts on Computational Mechanics). Amsterdam: Elsevier.

Google Scholar

Azad, S. (2015). A Study on Accelerating Time History Analysis of Bridges. M.Sc. dissertation, International Institute of Earthquake Engineering and Seismology (IIEES), Iran (In Persian).

Baiani, A. (2018). On the Possibility to Accelerate Time History Analysis of Buildings with Irregularities in Plan Because of Mass Distribution. M.Sc. Dissertation, University of Pooyandegan Danesh, Iran (in press in Persian).

Bastami, M. (2014). “A technique for more efficient time integration applied to seismic analysis of power substation equipment,” in Paper Presented at the 11th World Congress on Computational Mechanics (WCCM XI) (Barcelona).

Google Scholar

Bathe, K. (1996). Finite Element Procedures. Upper Saddle River, NJ: Prentice-Hall.

Google Scholar

Belytschko, T., Liu, W. K., and Moran, B. (2000). Nonlinear Finite Elements for Continua and Structures. New York, NY: John Wiley & Sons.

Google Scholar

Bergmeister, K. (2012). Brenner Base Tunnel under Construction. Available online at: http://www.tunnel-online.info/en/artikel/tunnel_2012-01_Brenner_Base_Tunnel_under_Construction_1370791.html

Besselink, B., Tabak, U., Lutowska, A., Van de Wouw, N., Nijmeijer, H., Rixen, D. J., et al. (2013). A comparison of model reduction techniques from structural dynamics, numerical mathematics and systems and control. J. Sound Vib. 332, 4403–4422. doi: 10.1016/j.jsv.2013.03.025

CrossRef Full Text | Google Scholar

Clough, R. W., and Penzien, J. (1993). Dynamics of Structures. Singapore: McGraw-Hill.

Google Scholar

Cook, R., Malkus, D., Plesha, M., and Witt, R. (2002). Concepts and Applications of Finite Element Analysis. New York, NY: John Wiley & Sons.

Google Scholar

Gao, Y., and Strang, G. (1989). Geometric nonlinearity: potential energy, complementary energy, and the gap function. Q. Appl. Math. 47, 487–504. doi: 10.1090/qam/1012271

CrossRef Full Text | Google Scholar

Garakaninezhad, A., and Moghadas, R. K. (2015). “On the performance of a technique to accelerate time integration when applied to space structures analyses,” in Paper Presented at the 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2015) (Crete Island).

Google Scholar

Gaylord, E. H., Gaylord, C. N., and Stallmeyer, J. E. (1997). Structural Engineering Handbook. New York, NY: McGraw-Hill.

Google Scholar

Ghondaghsaz, H. (2018). A Study on a Recent Technique for More Efficient Seismic Analysis Applied to Concrete and Steel Buildings. M.Sc. dissertation, Islamic azad, University West Tehran Branch, Tehran, (in Persian).

Hadad, A. (2015). Reducing Computational Costs in Time Integration Analyses of Buildings With Irregularities in Height Because of Mass. M.Sc. Dissertation, International Institute of Earthquake Engineering and Seismology (IIEES), Iran (In Persian).

Henrici, P. (1962). Discrete Variable Methods in Ordinary Differential Equations. Upper Saddle River, NJ: Prentice-Hall.

Google Scholar

Henrych, J. (1990). Finite Models and Methods of Dynamics in Structures. Amsterdam: Elsevier.

Google Scholar

Hughes, T. J. (1987). The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Upper Saddle River, NJ: Prentice-Hall.

Google Scholar

Hughes, T. J., Pister, K. S., and Taylor, R. L. (1979). Implicit-explicit finite elements in nonlinear transient analysis. Comput. Methods Appl. Mech. Eng. 17, 159–182. doi: 10.1016/0045-7825(79)90086-0

CrossRef Full Text | Google Scholar

McNamara, J. F. (1974). Solution schemes for problems of nonlinear structural dynamics. J. Pressure Vessel Technol. 96, 149–155. doi: 10.1115/1.3454158

CrossRef Full Text | Google Scholar

Monro, D. M. (1982). Fortran 77. Edward Arnold, UK.

Google Scholar

Nateghi, F., and Yakhchalian, M. (2011). “An investigation into the effectiveness of a technique proposed for reducing computational cost of time integration in the analysis of silos seismic behaviors,” in Paper presented at the 11th US National Congress on Computational Mechanics (USNCCM 2011) (Minneapolis, MN).

Google Scholar

NZS 1170 (2004). Structural Design Actions, Part 5: Earthquake Actions-New Zealand.

Sabzei, A. (2013). On the Performance of a Recent Technique For Seismic Analyses Computational Cost Reduction When Applied to Buildings Structural Systems. M.Sc. dissertation, International Institute of Earthquake Engineering and Seismology (IIEES), Iran (in Persian).

Soroushian, A. (2008). A technique for time integration analysis with steps larger than the excitation steps. Commun. Numer. Methods Eng. 24, 2087–2111. doi: 10.1002/cnm.1097

CrossRef Full Text | Google Scholar

Soroushian, A. (2010). “Proper Convergence a Concept New in Science and Important in Engineering,” in Paper Presented at the 4th International Conference from Scientific Computing to Computational Engineering (Athens), 7–10.

Google Scholar

Soroushian, A. (2017). “Integration step size and its adequate selection in analysis of structural systems against earthquakes,” in Computational Methods in Earthquake Engineering. Computational Methods in Applied Sciences, Vol. 3, eds M. Papadrakakis, V. Plevris, and N. Lagaros (Cham: Springer), 285–329. doi: 10.1007/978-3-319-47798-5_10

CrossRef Full Text | Google Scholar

Soroushian, A., and Farjoodi, J. (2003). More reliable responses for time integration analyses. Struct. Eng. Mech. 16, 219–240. doi: 10.12989/sem.2003.16.2.219

CrossRef Full Text | Google Scholar

Soroushian, A., Jahani Mehrnoosh, A., Zarabimanesh, Y., Ghondaghsaz, M., Baiani, A., and Zakizade, A. (2016). “On the performance of a computational cost reduction technique when applied to cooling towers transient analysis,” in Paper Presented at the 7th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS VII) (Crete Island).

Google Scholar

Soroushian, A., Zarabimanesh, Y., Soleymani, K., and Khalkhali, S. M. (2017). “A new technique for fractional enlargement of integration steps in transient analysis against digitized excitations,” in Paper Presented at the International Conference on Structural Engineering Dynamics (ICEDyn 2017) (Ericeira).

Google Scholar

Strikwerda, J. C. (1989). Finite Difference Schemes and Partial Differential Equations. Pacific Grove: Wadsworth & Books/Cole.

Google Scholar

Wriggers, P. (2002). Computational Contact Mechanics. New York, NY: John Wiley & Sons.

Google Scholar

Zarabimanesh, Y. (2017). On a Recent Technique for Reducing the Computational Costs in Time Integration Analyses When Applied to the Analysis of Milad Tower. M.Sc. dissertation, International Institute of Earthquake Engineering and Seismology (IIEES), Iran (In Persian).

Zhou, K. K., and Tamma, K. K. (2004). A new unified theory underlying time dependent first-order systems: a prelude to algorithms by design. Int. J. Numer. Meth. Eng. 60, 1699–1740. doi: 10.1002/nme.1019

CrossRef Full Text | Google Scholar

Zienkiewicz, O. C., and Taylor, R. L. (2005). The Finite Element Method for Solid and Structural Mechanics. Oxford: Elsevier.

Google Scholar