- Department of System Design Engineering, Keio University, Yokohama, Japan
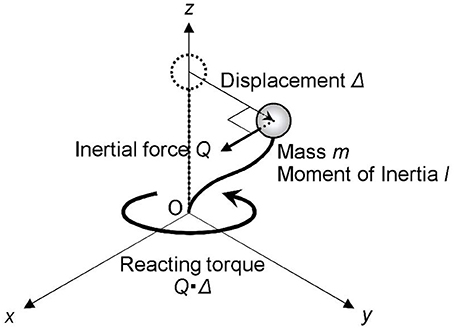
Eccentric distribution of stiffness, damping, and mass of a structure, and spatially non-uniform ground motion input to a long or large base mat of a structure are well-known causes of torsional response. We have discovered that the torque generated by horizontal displacement and perpendicular inertial force, which we call the Q-Δ effect, can be a cause of torsional response. We formulated the equation of motion of a single finite-size mass-linear elastic shear and torsion spring model and clarified the resonance condition of the torsional response to sinusoidal ground acceleration. Time-history response analysis verified that the torsional response forms beat and the maximum torsional response of the simulation result agrees with that theoretically predicted. Further time-history response analysis conducted of white noise ground acceleration showed that even one-directional white noise ground acceleration can induce torsional response in a linear elastic system without any structural eccentricity.
Introduction
Although torsional response induced by seismic ground motion has been investigated for more than 60 years, several factors still remain unclarified (Anagnostopoulos et al., 2015). As causes of the torsional response of buildings, researchers have studied eccentric distribution of stiffness (Georgoussis, 2009; Stathi et al., 2015), damping (Goel, 2000; Lin and Tsai, 2007), and the mass of a structure (Chandler and Hutchinson, 1986), in addition to spatially non-uniform or torsional ground motion input (De la Llera and Chopra, 1994; Heredia-Zavoni and Barranco, 1996; Basu and Giri, 2015; Falamarz-Sheikhabadi and Ghafory-Ashtiany, 2015; Gičev et al., 2015). A comprehensive review article has also been written by Anagnostopoulos et al. (2015). Therefore, their target buildings in general have an irregular, asymmetric structural property for the former perspective, which includes accidental eccentricity due to non-structural component or structural damage, and a long or large base mat that can incur phase difference of input ground motion for the latter. A few studies have also been conducted on the torsional response of symmetric buildings. For example, Tso (1975), Antonelli et al. (1981), and Pekau and Syamal (1984) studied the induction of torsional motion in symmetric structures with nonlinearity in the force-displacement relation of the lateral resisting elements. Cao et al. (2016, 2017) investigated the effects of near-fault pulse-like ground motions using a soil-foundation-structure system. Karayannis and Naoum (2018) studied an exceptional cause, asymmetric pounding with an adjacent building.
On the other hand, there are different powerful streams of studies on the P-Δ effect and rocking vibration (e.g., Wynhoven and Adams, 1972; Jennings and Bielak, 1973; Veletsos and Meek, 1974; Rutenberg, 1982; Akiyama, 1984; Bernal, 1987; Wilson and Habibullah, 1987; Uetani and Tagawa, 1992; MacRae, 1994; Tremblay et al., 1999; Aschheim and Hernández-Montes, 2003; Moghadam and Aziminejad, 2004; Humar et al., 2006; Deierlein et al., 2010; Yu et al., 2015). The P-Δ effect is a non-negligible overturning moment generated by dead loads and large lateral displacement. Rocking vibration is also induced by the overturning moment owing to the horizontal seismic force (inertial force) and the large height from the foundation to the point where the force is applied, in addition to foundation rocking caused by soil–structure interaction and/or incoherent ground motion. Flores et al. (2018) studied the amplification of torsional response due to the geometric nonlinearity effect of the gravity load.
From this moment-generating mechanism, we can infer torsional moment induction due to large lateral displacement and perpendicular inertial force (Figure 1). Although it has never been given significant focus, this effect might cause serious response amplification for high-rise buildings, which have large displacement under seismic excitation. In particular, as Japan has a high risk of large-magnitude earthquakes, which tend to generate broadband long-duration ground motion, it is crucial that the resonance of high-rise buildings be considered.
In this paper, we investigate this overlooked phenomenon, namely the Q-Δ effect, using a single-mass elastic model. The Q represents lateral force, which is querkraft in German, as conventionally used in mechanics. First, we formulate the equation of motion to model this phenomenon. Then, we derive the theoretical solution of response under sinusoidal wave input and clarify the condition that large torsional response appears. Finally, based on the condition, we demonstrate that single-directional white noise ground motion causes resonance of torsional mode using time-history response analysis.
Derivation of Conditions to Induce Torsional Response
Model and Equation of Motion
To investigate the fundamental principle of torsional response induction due to horizontal displacement and perpendicular inertial force, we utilize a single finite-size mass-linear elastic shear and torsion spring and damper model, which is an idealized model of a building, and derive the equation of motion under ground excitation. Here, we assume the linear elastic material property of columns, which is represented by a shear and torsion spring and damper, and geometric nonlinearity, i.e., large displacement of a floor slab, which is represented by a finite-size mass. Figure 2 shows the model and the displacement variables used. Each rectangle represents a floor slab with a mass m and moment of inertia I. The horizontal displacement of the floor slab is represented by x and y in the x- and y-axis directions, respectively, and the rotation angle θ around the z axis in the anti-clockwise direction from the x axis. A column with horizontal shear stiffness kx and ky in the x- and y-axis direction, and kθ for rotation around the z axis, connects the centroid G of the floor slab to the point O of the foundation on the ground surface. Similarly, we consider damping cx, cy, and cθ between the floor slab and ground. That is, we model the story stiffness and damping with linear springs and viscous dampers of three degrees of freedom. Without loss of generality, we assume kx ≥ ky. The system has the initial condition (x, y, θ) = (0, 0, 0) and at time t = 0 and is subject to ground acceleration (ẍ0, ÿ0, 0).
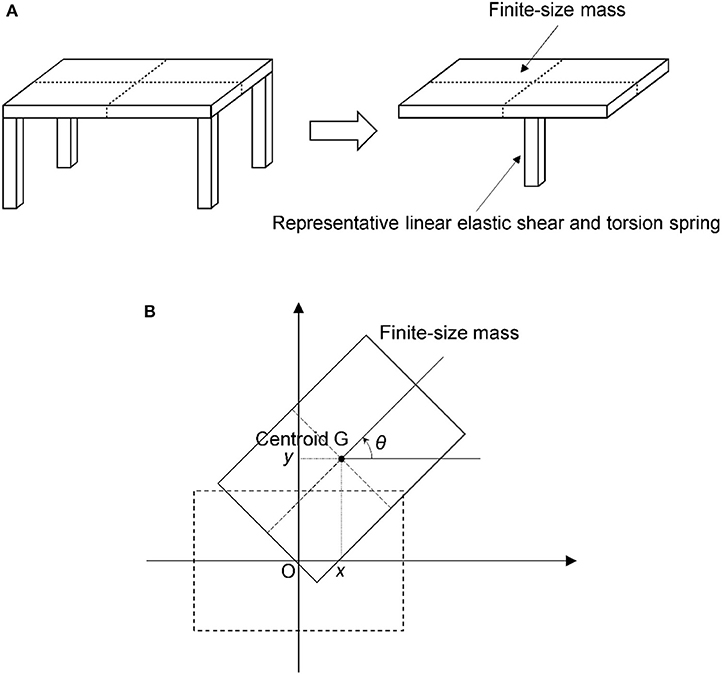
Figure 2. A single finite-size mass–linear elastic shear and torsion spring model. (A) Representative linear elastic shear and torsion spring, (B) Displacement variables.
With respect to translational displacements, the equation of motion is described as follows:
An inertial force perpendicular to the horizontal displacement generates a torsional moment M and its reaction moment −M at ground (foundation of the structure) point O. We define M taking a positive value counterclockwise around the z axis. M is calculated as follows:
Alternatively, we can calculate the moment M in another manner. Horizontal reaction forces Nx and Ny in the x and y direction, which are supporting the column at point O, satisfy equilibrium with the restoring and damping forces of a column;
Note that these reaction forces are the sum of non-conservative and conservative forces. These reaction forces at point O generate torsional moment M around the centroid G of the slab:
If Equations (1) and (2) are substituted into Equation (5), we can confirm that Equation (5) is identical to Equation (3).
Using moment M, the equation of motion in the rotational direction is given as follows:
We can summarize the equation of motion in matrices and vectors:
In the above equation, torsional moment (torque) generated by the inertial force is in the right side and we can regard this torque as an external moment of seismic force and perpendicular displacement.
The equations of motion are transformed into the following vibration equations:
where the natural circular frequencies
damping factors
and radius of gyration
Lx and Ly represent the length of the floor slab in the x and y directions, respectively, and we assume the slab has uniform density. Because we assume kx ≥ ky, natural frequencies in translational modes have the relation ωx ≥ ωy.
Steady-State Response to Unit Complex Ground Acceleration
We input the following unit complex ground acceleration into the target system:
where i is an imaginary unit, and px and py are circular frequencies of ground acceleration in the x and y directions, respectively. The vibrations of equations in the translational directions are mutually independent and we first focus on steady-state response in the x direction. The solution to response x can be assumed in the following form:
where X represents the complex amplitude of the steady-state response in the x direction. By substituting this equation into Equation (8), we obtain
Therefore, complex amplitude X is given by
where |X| and ϕx represent the absolute value and phase of X:
In the same manner, the steady-state response in the y direction is obtained as follows:
With respect to the rotational direction, we first calculate M/I in Equation (10).
Alternatively, we can obtain a simpler expression using Equation (10):
where
By substituting this solution into the rotational vibration Equation (10),
Because the system is linear also in the rotational direction, the steady-state rotational response under complex ground acceleration with a circular frequency of px+py can be solved as follows:
where
and
From this solution, it is clear that the torsional response has an amplitude proportional to that of the translational responses in two orthogonal directions and has a circular frequency of px+py; i.e., the summation of circular frequencies of ground acceleration in two orthogonal directions.
Derivation of Torsional Mode Resonance Condition Under Unit Complex Ground Acceleration
Suppose that the damping factors ζx and ζy are small, resonance of translational responses occur when ground acceleration circular frequency is identical to natural circular frequency:
In this case, the response amplitudes are approximated as follows:
Equation (26) is transformed as follows:
Now, we introduce an assumption that damping factors are the same ζ in three directions:
Then, Equation (38) is transformed into
With respect to torsional response, Equations (31), (36a,b) give the resonance condition:
In this case, |Θ| is approximated as follows:
Finally, the torsional response amplitude |S| in the resonance state is given by
It should be noted that, when a system has the same natural circular frequency in two translational directions, i.e., ωx = ωy, torsional response is not induced because |S| is zero.
If the resonance condition is rewritten by using system natural periods Tx, Ty, Tθ and ground motion period T0x, T0y,
where
From Equation (45), we obtain
Steady-State Response to Unit Sinusoidal Ground Acceleration
Next, we consider unit sinusoidal ground acceleration. The input ground motions are defined as follows:
where px and py are the circular frequency of the input sine waves. Steady-state translational responses are derived from the result of the unit complex ground acceleration case:
By taking the time derivatives of these equations, we obtain
Using these equations, we can calculate the following products:
The right side of term M/I in Equation (10) is then calculated as follows:
where
Therefore, the rotational vibration equation is given by
Because the right side of Equation (64) is the real part of the summation of the complex external forces with two different circular frequencies, we can derive the torsional response in the same manner as in section Steady-State Response to Unit Complex Ground Acceleration:
where
Equation (65) can be described in a different way:
We observe that torsional response is proportional to the amplitude of the translational response in two orthogonal directions and its form is the superposition of two sine waves with circular frequencies px + py and px − py. This is easily understood because the ground acceleration consists of complex ground accelerations with circular frequencies of px and −px in the x direction and py and −py in the y direction. Further, on the basis of Equation (29), the torsional response is given by the combination of two circular frequencies in the orthogonal directions; i.e., ±(px + py) and ±(px − py).
Derivation of Torsional Mode Resonance Condition Under Sinusoidal Ground Acceleration
To determine the condition of torsional mode resonance under sinusoidal ground acceleration, we assume that the damping factors are small and the translational mode resonance is occurring in two directions owing to the ground acceleration frequency being identical to the natural circular frequency:
The amplitudes of the translational responses can be approximated as follows:
Using the following formula:
where α is an additional phase introduced by calculation of trigonometric functions, the right side of Equation (78) can be transformed as follows:
The result implies that the torsional response is a beat, of which amplitude changes periodically. The maximum amplitude is estimated by
Here, we introduce another assumption that the damping factors are identical:
Then, Equations (58) and (60) are simplified as follows:
This result suggests that large torsional response occurs when the difference between two natural frequencies of orthogonal translational modes is large. In addition, |A1| < |A2| because ωx > 0 and ωy > 0.
Equations (70) and (76) with respect to |Θ1| and |Θ2| give alternative conditions of torsional mode resonance as follows:
Equations (87a,b) correspond to the resonance conditions of the first and second terms in Equation (83), respectively. To distinguish these two natural circular frequencies to cause resonance, we name the former and latter ωθ+ and ωθ−, respectively.
If the condition is rewritten using natural periods,
where
Verification Based on Numerical Simulation
Simulation of Response to Sinusoidal Ground Acceleration
Large torsional response due to resonance is predicted when the natural period of torsional mode satisfies Equations (88c) or (88d) and two orthogonal translational modes also cause resonance. We verify this prediction via numerical simulation below.
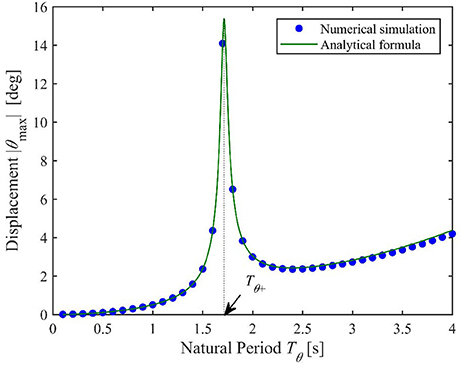
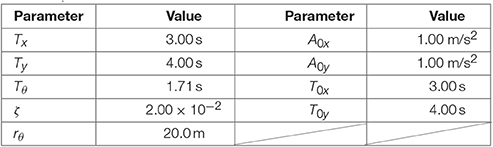
We use a model with and rθ = 20.0 m. The estimated maximum torsional response of Equation (83) can be rewritten as a function of Tθ = 2π/ωθ:
Because of the assumption that translational modes cause resonance, the values of |X| and |Y| are calculated using Equations (80a,b). Equations (85) and (86) indicate that |A1| and |A2| are independent of ωθ; i.e., Tθ. Therefore, the relation between the estimated maximum displacement of torsional response |θmax| and natural period of torsional mode Tθ can be depicted as the green curve in Figure 3.
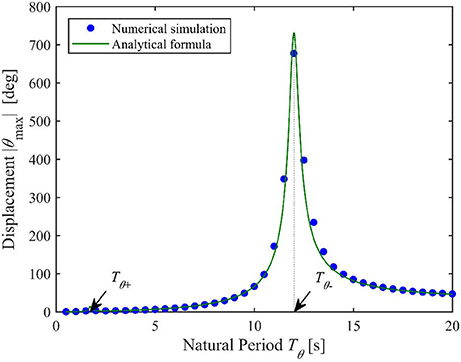
Figure 3. Relation between the maximum displacement of torsional response |θmax| and the natural period of torsional mode Tθ.
From Equations (88c,d), the torsional response causes resonance when Tθ = Tθ+ = 1.71 s or Tθ− = 12.0 s. Therefore, the condition Equation (88d) gives quite a larger response. However, when looking at a database of natural periods of actual existing buildings (Architectural Institute of Japan., 2000), the natural period of torsional mode, Tθ, is generally smaller than that of the translational modes, Tx and Ty. To check the detail of the period range of 0 to 4 s, Figure 4 shows a zoomed-up graph. At this range, condition (88c) gives the largest maximum response.
The time-history analysis of vibration Equations (8–10) are conducted by using the Newmark β method with the parameter β = 1/6 and time step interval Δt = 0.01 s. We first conduct time integration of Equations (8, 9). Then, the torsional response is calculated by using the obtained translational responses.
Input ground accelerations are given by the following sine waves:
The parameters of the target model and ground accelerations are shown in Table 1, in which Tθ is determined based on the resonance condition of torsional mode, Equations (88a–c).
Figure 5A shows input ground motion and Figure 5B the simulated displacement response. The response gradually shifts to a steady state. We can verify that the torsional response (red line in Figures 5B,C) shapes a beat and the maximum response matches the theoretically predicted value of 15.4° shown in Figure 4.
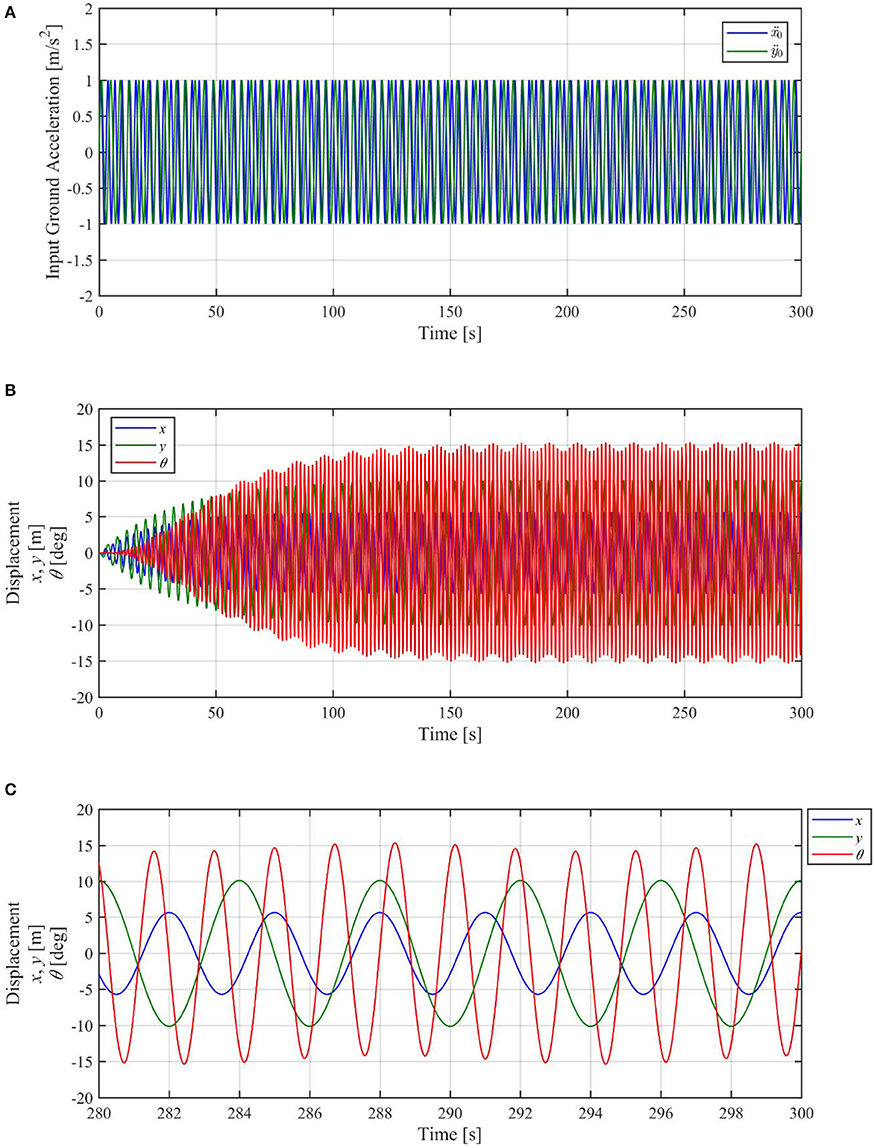
Figure 5. Time-history analysis result of displacement response to sinusoidal ground acceleration. (A) Input ground motion, (B) Displacement response, (C) Displacement response (zoomed-up graph).
To examine the validity of Equation (90), other models with a different Tθ value were simulated and the maximum responses in a duration of 300 s recorded. The results for Tθ∈[0.5 s, 1 s, 1.5 s, …, 20 s] are shown by blue points in Figure 3. Similarly, the results for Tθ∈[0.1 s, 0.2 s, 0.3 s, …, 4 s] are shown in Figure 4. The numerical simulation results are virtually identical to the predicted values.
Simulation of Response to White Noise Ground Acceleration
Seismic ground motion is often modeled by filtered white noise. White noise, which has a flat power spectrum over all frequencies, can excite translational modes with any natural frequency. Therefore, it could excite two orthogonal translational modes with different natural frequencies and consequently could induce torsional response. We first input uncorrelated white noise ground accelerations in the x and y directions, as shown in Figure 6A. The power spectrum density of both accelerations is Sx0 = Sy0 = 1.00 m2/s3. Figure 6B shows the simulation results. It can be seen that the torsional response (red line) is induced by uncorrelated two-directional white noise ground acceleration.
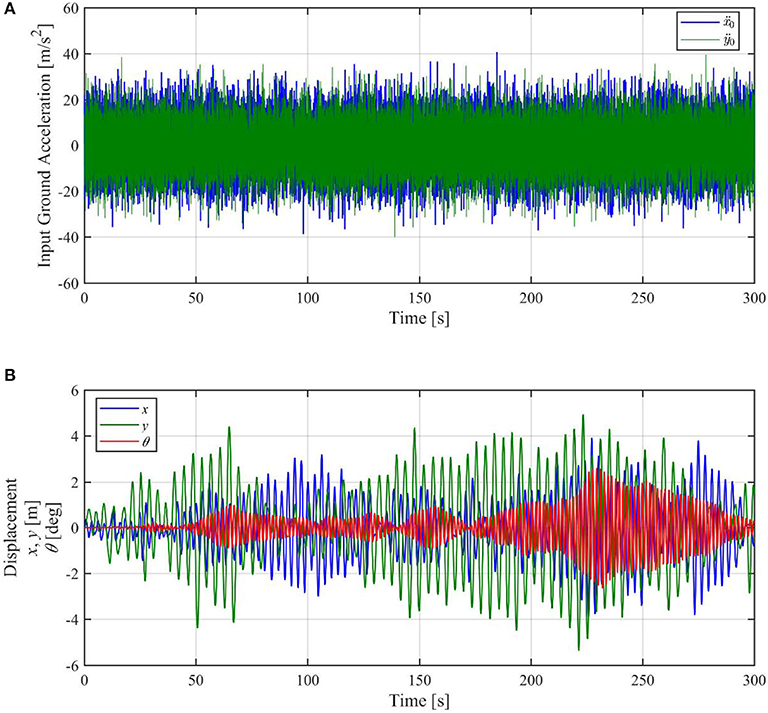
Figure 6. Time-history analysis result of displacement response to uncorrelated two-directional white noise ground acceleration. (A) Input ground acceleration (B) Displacement response.
Next, we input fully correlated white noise ground accelerations in the x and y directions in the same manner, as shown in Figure 7A. This is equivalent to inputting one-directional white noise ground acceleration in the 45° direction from the x axis. The power spectrum density of the accelerations is Sx0 = Sy0 = 0.707 m2/s3; i.e., 1.00 m2/s3 in the excitation direction. The result is shown in Figure 7B, where it can be seen that the maximum torsional response exceeds 2.0° under the used input ground acceleration. We thus confirm that even one-directional ground motion can induce the torsional response of a symmetric structure without any eccentricity.
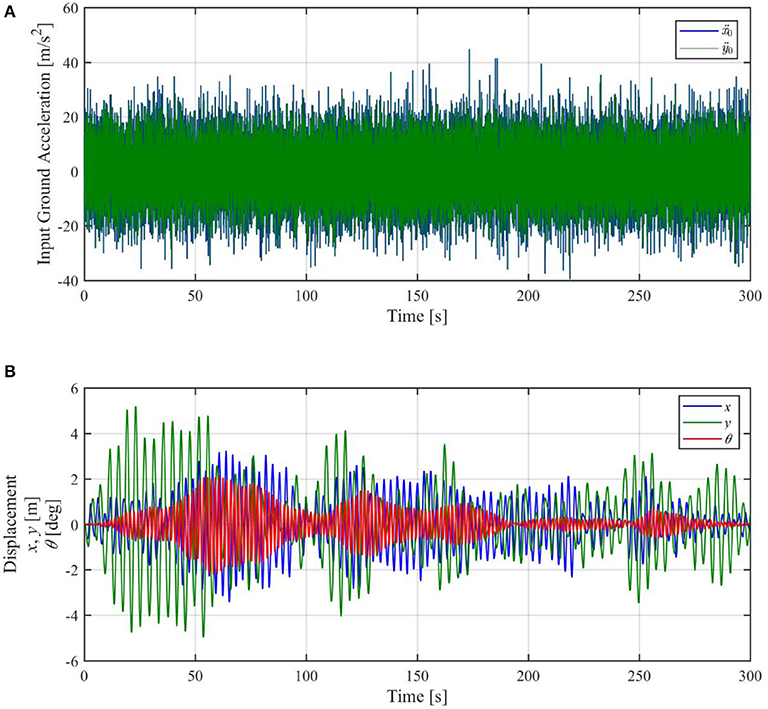
Figure 7. Time-history analysis result of displacement response to one-directional (45° direction from the x axis) white noise ground acceleration. (A) Input ground acceleration, (B) Displacement response.
Conclusions
In past studies, researchers hypothesized that torsional response is induced by eccentric distribution of stiffness, damping, or mass of a structure, or spatially non-uniform ground motion input to the long or large base mat of a structure. In this paper, we showed that the torque generated by horizontal displacement and perpendicular inertial force, which we call the Q-Δ effect, has an overlooked cause of torsional response. We formulated the equation of motion of a single finite-size mass–linear elastic shear and torsion spring and damper model, which is an idealized model of a building and revealed the resonance condition of torsional response to sinusoidal ground acceleration. Time-history response analysis was conducted and we verified that the torsional response forms a beat and the maximum torsional response of the simulation result agrees with that theoretically predicted. The model used had natural periods of 3.00 s and 4.00 s for the translational modes and 1.71 s for the torsional mode, which was predicted to cause torsional resonance, with 2% damping. The maximum torsional response reached 15.4° under two-directional sinusoidal ground accelerations with an amplitude of 1.00 m/s2 and periods identical to the natural periods of the translational modes. We further conducted time-history response analysis of white noise ground acceleration and discovered that even one-directional white noise ground acceleration can induce the torsional response of a linear elastic system without any structural eccentricity. In this case, the torsional response exceeded 2.0° under the input white noise ground acceleration with a power spectrum density of 1.00 m2/s3.
Our future tasks are as follows:
• We have to expand the theory to a multi-story system and a system with structural eccentricity. In our theory, the natural frequency difference in two translational modes is necessary for induction of torsional response, and we have to check the necessity in consideration of higher modes.
• The maximum response should be estimated in a probabilistic manner and the prediction formula should be developed.
• We also have to expand the theory to a different input ground motion model, such as colored noise and non-stationary models.
• Further validation studies are also required, such as finite element analysis considering geometric nonlinearity and shaking table experiments.
• We also need to conduct a survey on the seismic damage risk of existing structures due to torsional response induced by the Q-Δ effect.
• The building code may need to be amended to consider the Q-Δ effect properly, and in this case, effective revision has to be studied.
Author Contributions
MK constructed the theoretical framework. MK and HY derived the formulae and conducted the numerical simulation.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgements
This research was financially supported by a Japan Society for the Promotion of Science KAKENHI Grant Number 16H04455.
References
Akiyama, H. (1984). P-Δ effects on seismic strength of multistory steel frames. J Struct. Construct. Eng. 340, 1–16.
Anagnostopoulos, S. A., Kyrkos, M. T., and Stathopoulos, K. G. (2015). Earthquake induced torsion in buildings: critical review and state of the art. Earthquakes Struct. 8, 305–377. doi: 10.12989/eas.2015.8.2.305
Antonelli, R. G., Meyer, K. J., and Oppenheim, I. J. (1981). Torsional instability in structures. Earthquake Eng. Struct. Dyn. 9, 221–237. doi: 10.1002/eqe.4290090304
Architectural Institute of Japan. (2000). Damping in Buildings. Tokyo: Architectural Institute of Japan.
Aschheim, M., and Hernández-Montes, E. (2003). The representation of P-Δ effects using Yield Point Spectra. Eng. Struct. 25, 1387–1396. doi: 10.1016/S0141-0296(03)00106-8
Basu, D., and Giri, S. (2015). Accidental eccentricity in multistory buildings due to torsional ground motion. Bull. Earthquake Eng. 13, 3779–3808. doi: 10.1007/s10518-015-9788-0
Bernal, D. (1987). Amplification factor for inelastic dynamic P-Δ effects in earthquake analysis. Earthquake Eng. Struct. Dyn. 15, 635–651. doi: 10.1002/eqe.4290150508
Cao, Y., Mavroeidis, G. P., Meza-Fajardo, K. C., and Papageorgiou, A. S. (2017). Accidental eccentricity in symmetric buildings due to wave passage effects arising from near-fault pulse-like ground motions. Earthquake Eng. Struct. Dyn. 46, 2185–2207. doi: 10.1002/eqe.2901
Cao, Y., Meza-Fajardo, K. C., Mavroeidis, G. P., and Papageorgiou, A. S. (2016). Effects of wave passage on torsional response of symmetric buildings subjected to near-fault pulse-like ground motions. Soil Dyn. Earthquake Eng. 88, 109–123. doi: 10.1016/j.soildyn.2016.04.001
Chandler, A. M., and Hutchinson, G. L. (1986). Torsional coupling effects in the earthquake response of asymmetric buildings. Eng. Struct. 8, 222–236. doi: 10.1016/0141-0296(86)90030-1
De la Llera, J. C., and Chopra, A. K. (1994). Accidental torsion in buildings due to base rotational excitation. Earthquake Eng. Struct. Dyn. 23, 1003–1021. doi: 10.1002/eqe.4290230906
Deierlein, G. G., Reinhorn, A. M., and Willford, M. R. (2010). Nonlinear Structural Analysis for Seismic Design: A Guide for Practicing Engineers. NEHRP Seismic Design Technical Brief No. 4, NIST GCR 10-917-5. Gaithersburg, MD: National Institute of Standards and Technology.
Falamarz-Sheikhabadi, M. R., and Ghafory-Ashtiany, M. (2015). Rotational components in structural loading. Soil Dyn. Earthquake Eng. 75, 220–233. doi: 10.1016/j.soildyn.2015.04.012
Flores, F., Charney, F. A., and Lopez-Garcia, D. (2018). The influence of accidental torsion on the inelastic dynamic response of buildings during earthquakes. Earthquake Spectra 34, 21–53. doi: 10.1193/100516EQS169M
Georgoussis, G. (2009). An alternative approach for assessing eccentricities in asymmetric multi-story buildings: 1. Elastic systems. Struct. Design Tall Special Build. 18, 181–202. doi: 10.1002/tal.401
Gičev, V., Trifunac, M. D., and Orbović, N. (2015). Translation, torsion, and wave excitation of a building during soil-structure interaction excited by an earthquake SH pulse. Soil Dyn. Earthquake Eng. 77, 391–401. doi: 10.1016/j.soildyn.2015.04.020
Goel, R. K. (2000). Seismic behaviour of asymmetric buildings with supplemental damping. Earthquake Eng. Struct. Dyn. 29, 461–480. doi: 10.1002/(SICI)1096-9845(200004)29:4<461::AID-EQE917>3.0.CO;2-6
Heredia-Zavoni, E., and Barranco, F. (1996). Torsion in symmetric structures due to ground-motion spatial variation. J. Eng. Mech. 122, 834–843. doi: 10.1061/(ASCE)0733-9399(1996)122:9(834)
Humar, J., Mahgoub, M., and Ghorbanie-Asl, M. (2006). Effect of second-order forces on seismic responses. Can. J. Civil Eng. 33, 692–706. doi: 10.1139/l05-119
Jennings, P. C., and Bielak, J. (1973). Dynamics of building-soil interaction. Bull. Seismol. Soc. Am. 63, 9–48.
Karayannis, C. G., and Naoum, M. C. (2018). Torsional behavior of multistory RC frame structures due to asymmetric seismic interaction. Eng. Struct. 163, 93–111. doi: 10.1016/j.engstruct.2018.02.038
Lin, J. L., and Tsai, K. C. (2007). Simplified seismic analysis of one-way asymmetric elastic systems with supplemental damping. Earthquake Eng. Struct. Dyn. 36, 783–800. doi: 10.1002/eqe.653
MacRae, G. A. (1994). P-Δ effects on single-degree-of-freedom structures in earthquakes. Earthquake Spectra 10, 539–568. doi: 10.1193/1.1585788
Moghadam, A. S., and Aziminejad, A. (2004). “Interaction of torsion and p-delta effects in tall buildings,” in Proceedings of 13th World Conference on Earthquake Engineering (Vancouver, BC).
Pekau, O. A., and Syamal, P. K. (1984). Non-linear torsional coupling in symmetric structures. J. Sound Vibrat. 94, 1–18. doi: 10.1016/S0022-460X(84)80002-4
Rutenberg, A. (1982). Simplified p-delta analysis for asymmetric structures. ASCE J. Struct. Div. 108, 1995–2013.
Stathi, C. G., Bakas, N. P., Lagaros, N. D., and Papadrakakis, M. (2015). Ratio of Torsion (ROT): An index for assessing the global induced torsion in plan irregular buildings. Earthquakes Struct. 9, 145–171. doi: 10.12989/eas.2015.9.1.145
Tremblay, R., Côté, B., and Léger, P. (1999). An evaluation of P-Δ amplification factors in multistorey steel moment resisting frames. Can. J. Civil Eng. 26, 535–548. doi: 10.1139/l99-015
Tso, W. K. (1975). Induced torsional oscillations in symmetrical structures. Earthquake Eng. Struct. Dyn. 3, 337–346. doi: 10.1002/eqe.4290030404
Uetani, K., and Tagawa, H. (1992). Deformation concentration phenomena in the process of dynamic collapse of weak-beam-type frames. J. Struct. Const. Eng. 483, 51–60.
Veletsos, A. S., and Meek, J. W. (1974). Dynamic behaviour of building-foundation systems. Earthquake Eng. Struct. Dyn. 3, 121–138. doi: 10.1002/eqe.4290030203
Wilson, E. L., and Habibullah, A. (1987). Static and dynamic analysis of multi-story buildings, including p-delta effects. Earthquake Spectra 3, 289–298. doi: 10.1193/1.1585429
Wynhoven, J. H., and Adams, P. F. (1972). Behavior of structures under loads causing torsion. ASCE J. Struct. Div. 98, 1361–1376.
Keywords: torsional response, Q-Δ effect, geometric nonlinearity, large displacement, lateral force, high-rise building
Citation: Kohiyama M and Yokoyama H (2018) Torsional Response Induced by Lateral Displacement and Inertial Force. Front. Built Environ. 4:38. doi: 10.3389/fbuil.2018.00038
Received: 24 March 2018; Accepted: 29 June 2018;
Published: 31 July 2018.
Edited by:
Arturo Tena-Colunga, Universidad Autónoma Metropolitana, MexicoReviewed by:
Luigi Di Sarno, University of Sannio, ItalyGeorge C. Tsiatas, University of Patras, Greece
Copyright © 2018 Kohiyama and Yokoyama. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Masayuki Kohiyama, a29oaXlhbWFAc2Qua2Vpby5hYy5qcA==
 Masayuki Kohiyama
Masayuki Kohiyama Hiroki Yokoyama
Hiroki Yokoyama