Ecological Validity of Impulsive Choice: Consequences of Profitability-Based Short-Sighted Evaluation in the Producer-Scrounger Resource Competition

Introduction

Spencer introduced the idea of “survival of the fittest” in “The Principles of Biology” (1864), and Darwin adopted this term in his 5th edition of “The Origin of Species” (1869). A naïve biological thinking might therefore be that only optimal individuals have been selected for survival. If it was, we might find a monochromatic world in which only a few fittest phenotypes predominate. Conversely, nature is full of diverse organisms with distinct behavioral phenotypes, even within a sympatric group of animals of the same species. We must consider some adaptive processes that make animals appropriately deviate from the optimality. Deviations due to social inter-individual interaction could be one of such critical processes. In this report, we focus on social foraging behavior as it allows us to theoretically and empirically make quantitative examinations on issues of optimality. Through introducing ecological theories of foraging, we argue that social facilitation and enhanced choice impulsiveness could be described as adaptive deviations.

Optimal Foraging, Profitability, and Intertemporal Choices

Optimal Diet Menu Model and Impulsive Choices

Classical theories usually assume that optimal foragers maximize the long-term averaged gain rate. Foragers explore food (searching time, abbreviated as T_s) and exploit it (consuming or handling time, T_h), so that the gain rate R is given for E_f (net energy gain) as a substitution variable for fitness [1].

$\begin{array}{l}R=\frac{E_f}{T_s+T_h}\end{array}$

As initially formulated as Holling's disc equation [2] and subsequently by Charnov [3] in his diet menu model, optimal foragers must maximize R. Assuming the stochastic nature of food resources, Charnov reached a somewhat paradoxical conclusion that the R-maximizer must make decisions (i.e., action choice between attacking or passing-over) based on short-sighted estimation of profitability e/h, where e represents energetic gain and h handling time for the encountered food item. Namely, they attack the food if the expected profitability exceeds the lost opportunity, that is the potential food gained by passing over (or giving up) the encountered food item. We should consider (1) prospective (expected) profitability of the food and (2) highly uncertain lost-opportunity, the latter of which may be approximated by the average gain rate they have had (Figure 1A left).

FIGURE 1

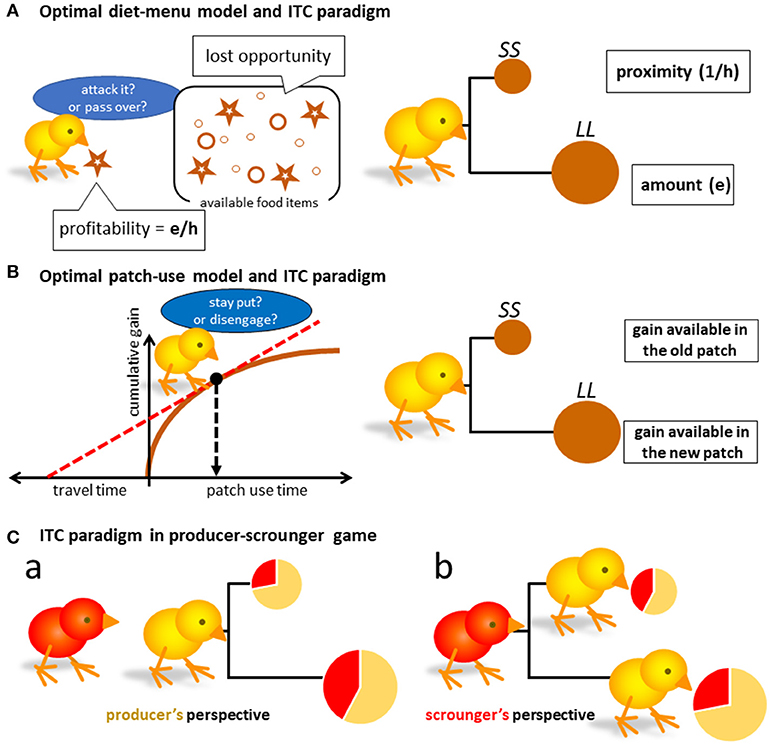
Figure 1. Possible isomorphism between optimal foraging theories and the intertemporal choice paradigm (A,B), which represent the optimal diet-menu model and the patch-use model, respectively. SS denotes a small and short delay reward, and LL a large and long delay alternative. Though the menu model (A) can be translated to the intertemporal choice (ITC) paradigm, the latter patch-use behavior cannot. In addition to the classical frameworks of optimal theories, we must address to the social foraging situation (Ca,b) to understand what the results of ITC tests could mean in terms of ecology.

As profitability is the product of gain (e) and proximity (1/h), the foraging choice may be isomorphic to the intertemporal choice (ITC) paradigm widely adopted to study impulsive/self-control issues (Ainslie-Rachalin theory [4]; Figure 1A right). Here, a set of two options {SS, LL} is given as:

$\begin{array}{l}SS=(e_1,h_1^{-1})LL=(e_2,h_2^{-1}),\text{ where }(e_1<e_2)\cap (h_1^{-1}>h_2^{-1}).\end{array}$

Based on behaviors in the ITC task [5–7], we formulated simple pico-economics for chicks in terms of profitability-based behaviors [8]. Briefly, as chicks feed on grain particles with small e, they must make h small by adopting highly impulsive choices, so that a certain level of profitability (e/h) is achieved. Choice impulsiveness does not necessarily represent internal anomalies in the machineries, but can be an adaptive trait with external (ecological) validity. An extreme case of such foraging economics is found in star-nosed mole rats [9], where the handling time was as short as 120 ms for the tiny food particles they eat. Hyperbolic discounting of future rewards is assumed to be a corollary to the profitability rule, simply because h includes the delay time for food. However, the zero-one rule (another principal prediction derived from the menu model [1]) is not met in many empirical studies including chicks. Instead, matching to the relative profitability has been the norm in most cases. Applicability of the menu model is thus limited.

Optimal Patch Use Model (Marginal Value Theorem) and Decision of Disengagements

Charnov proposed another important idea, the optimal patch-use model, which is based on marginal value theorem [10] (Figure 1B left). He assumes a single forager that sequentially visits a series of food patches. The model is characterized by (1) unevenly distributed food items in patches, and (2) resource depletion by the forager's consumption, as the convex curve of cumulative gain illustrates. The optimal forager must disengage from the patch at a point where gain rate is maximized (indicated by slope of the dashed red line in Figure 1B left) by action selection. If staying put in the patch, the forager will find the next food item in a short period of time. If disengaging, it must invest considerable time to find the new patch, which is more beneficial than the food item available in the old patch. Here again, the choice of actions might be translated to the intertemporal choice of options (Figure 1B right).

The possible commonality between the patch-use behavior and the ITC task has been challenged both theoretically and empirically [11–18]. So far, the foraging behavior cannot be translated to the ITC task, or these are simply not compatible. Actually, animals are less patient in the ITC task compared with their behaviors in natural foraging situations, and the temporal discounting measured in ITC task does not fit well with the decision to disengage. The underlying decision mechanism is also distinct, as pharmacological treatment using selective serotonin reuptake inhibitor (SSRI, fluvoxamine) suppressed impulsive choices but delayed the disengagement, contrary to the prediction based on the commonality [19]. Furthermore, the impulsivity measure can drastically change depending on how subjects are informed of the relevant parameters, such as the time after the food option was consumed (so-called post-reward delay) [7, 20]. Interspecies comparisons suggest a clear dependency on ecological factors such as diet preference [21, 22], but these factors do not uniquely characterize impulsivity of each species.

The ITC Paradigm in Social Foraging Situations

Producer-Scrounger Resource Conflict

Though these models may explain a single forager's behavior, we must consider that foraging is generally a social event, and animals compete and/or cooperate in both exploration and exploitation phases [23]. As the foragers' payoffs are mutually interdependent, individual decisions toward optimization inevitably result in sub-optimal outcome. To avoid starvation, animals should rather adopt a mixed strategy such as kleptoparasitism, which comprises producer and scrounger tactics [24]. Here, producers search and find food, and scroungers take free ride on the producer's discovery. If foragers freely change between the two alternative tactics, a stable equilibrium emerges at the point where the producer's gain is on par with the scrounger's. The validity of this framework has been shown in various animal studies [25–27].

What if the social foraging situation appears in the ITC paradigm? Intuitively, the producer chooses the more proximate food option, if the producer's share is higher for that proximate option (Figures 1Ca). On the other hand, the scrounger chooses the more proximate producer by the same token (Figures 1Cb). Under some circumstances, impulsive (or time-preference based) choices can be more beneficial. In the following sections, we will examine these possibilities by constructing analytical model and numerical calculation based on empirically-obtained parameters of behavior.

Rather than a mixed group composed of producers and scroungers, we presume a homogeneous group of opportunistic foragers that produce and scrounge simultaneously. In addition, we focus only on what the producing foragers gain. To produce food in nature, the foragers must pay a certain cost (such as traveling time, energy, and vigilance for food search) and make choices, whereas scroungers take free ride without paying the cost. We therefore assumed that only the producing foragers would update the food memory (value of food options), whereas the scroungers would not. We also disregard the cost and examine only the gain. Furthermore, foragers are assumed to exhaust all the food in a patch they find, rather than to disengage midway as the marginal value theorem assumes. As will be shown below, predictions based on these lines of simplification fit well with the behaviors of chicks that forage in densely packed flocks.

Assumptions

A pair of opportunistic foragers are assumed in a patchy food condition (Figure 2). When one forager encounters a patch comprising sharable food (F), it acts as producer (P), and rushes to F at a constant running speed v. Another forager immediately detects F discovered by P, acts as scrounger (S), and rushes to F at the same speed v. It might be possible to assume that S starts rushing to F only after P reaches F. We however assume that S rushes to P as soon as P rushes to F, because chicks run in response to the companion's (competitor's) running even before the companion starts to consume the food (social facilitation of running, [28]). Pecking food is also facilitated by companion's pecking (local enhancement), but the facilitated pecking is not causally linked with the facilitated running. Chicks run for other's run, and peck for other's peck, but these two types of facilitation are separate processes [29]. P is located closer to F (at distance d > 0) than S is, and S is at distance δ > 0 from P. The time required for each player's decision is short and therefore ignored.

A: amount of food items in a patch

d: distance between F and P

δ: distance between P and S

v: running velocity of P and S

According to one of the representative frameworks developed in social foraging theory [24], we assume a non-ephemeral food patch F (Figure 2A). We assume that each forager has a fixed speed of food consumption (s, amount per time per individual). As soon as P reaches F after a delay (D), the patch F supplies a finite amount of food (A) at once, and P starts to consume F at the speed s. P monopolizes F for a period (T) until S arrives at F at the point denoted as Φ. No conflict occurs between P and S, and F is thereafter consumed at twice the speed (2s) until F is exhausted at Ω. P's gain rate therefore does not diminish by sharing food with S. We may otherwise assume an ephemeral food patch that supplies food by itself at a rapidly declining rate. In such a patch type, the finder's share would be higher in favor of P's gain. In the following, however, we focus only on the non-ephemeral type for simplicity.

FIGURE 2

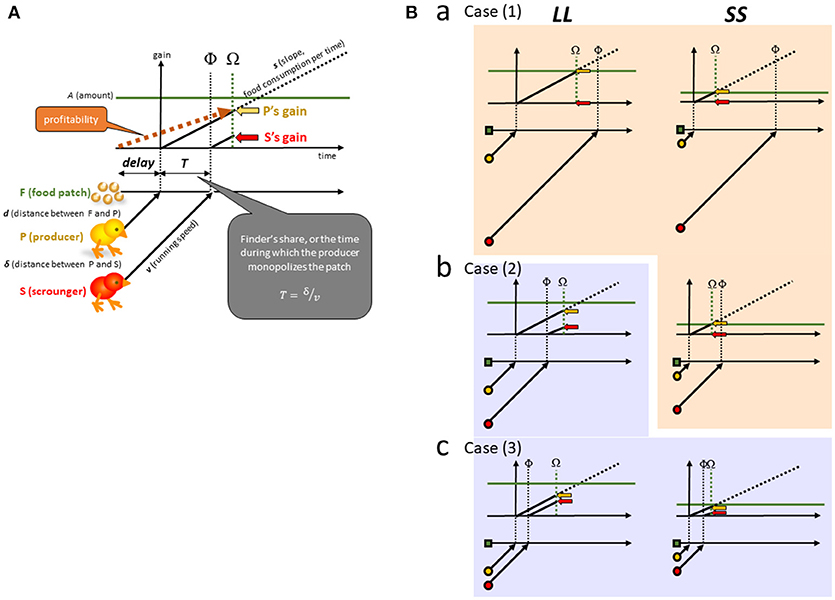
Figure 2. (A) A group comprising two opportunistic foragers is assumed. Each of the two foragers searches for food, and if one finds food (F), it acts a producing individual (P). Another forager immediately detects the discovery and rushes to P as a scrounging individual (S). A food patch of finite amount (A) is placed at a long distance (d) from P, representing the LL option (left columns). A food patch of a smaller amount at a short distance represents the SS option (right columns). (B) We consider three levels of scrounging as long [Ba; Case (1)], intermediate [Bb; Case (2)] and short [Bc; Case (3)] distances between P and S (δ). In Case (1), scrounging does not occur for both LL and SS. In Case (2), scrounging occurs only for LL. In Case (3), scrounging occur for both LL and SS. Scrounging inevitably reduces the P's finder's share, or the time during which P monopolizes the food (T).

The delay D and the finder's share (monopolizing time by P, denoted as T) are given as;

$\begin{array}{l}D=\frac{d}{v}\\ T=\frac{\delta }{v}\end{array}$

If Φ follows Ω, the food patch is exhausted by P before S arrives. This situation is met when

$\begin{array}{ll}\frac{A}{s}\le T=\frac{\delta }{v}& (1)\end{array}$

or

$\begin{array}{ll}A\le \frac{s\delta }{v}=sT& (1\prime )\end{array}$

If otherwise and Φ precedes Ω, the food patch is shared after Φ.

Profitability is illustrated as the slope of gain at Ω (dashed brown line with an arrow in Figure 2A) for each P (yellow arrow with a dashed line). We assume that foragers stay at F until Ω, when the food is exhausted. Depending on whether scrounging occurs, the profitability that P gains is given by the prof_p functions as;

$\begin{array}{ll}\text{If }\Phi \text{ follows }\Omega ,pro{f}_P=\frac{A}{D+A/s}& (2)\end{array}$

$\begin{array}{ll}\text{If }\Phi \text{precedes }\Omega ,pro{f}_P=\frac{A+sT}{2D+T+A/s}& (3)\end{array}$

Analysis of the Model

We mathematically examine the conditions where SS has a higher profitability than LL. As the inequality (1′) predicts, following 3 cases are considered;

Case (1); no scrounging for both SS and LL

$\begin{array}{ll}{A}_{SS}<A_{LL}\le sT& (4)\end{array}$

Case (2); scrounging for LL but not for SS

$\begin{array}{ll}{A}_{SS}\le sT<A_{LL}& (5)\end{array}$

Case (3); scrounging for both LL and SS

$\begin{array}{ll}sT<A_{SS}<A_{LL}& (6)\end{array}$

Here, A_SS and A_LL denote the amount of SS and LL, respectively. Similarly, the delay D for SS and LL is denoted as D_SS and D_LL. By definition,

$\begin{array}{l}{A}_{SS}<A_{LL}and{D}_{SS}<D_{LL}\end{array}$

These cases are schematically illustrated in Figure 2B for different δ for levels of scrounging, Ba for case (1), Bb for case (2), and Bc for case (3). In the following, we will show conditions where

$\begin{array}{ll}pro{f}_p(SS)>pro{f}_p(LL)& (7)\end{array}$

holds.

Case (1)

According to the formulae (2), the inequality formula (4) is given as;

$\begin{array}{ll}\frac{A_{SS}}{D_{SS}+A_{SS}/s}>\frac{A_{LL}}{D_{LL}+A_{LL}/s}& (8)\end{array}$

which is equivalent for ∀s > 0 to a simpler form;

$\begin{array}{ll}\frac{A_{SS}}{D_{SS}}>\frac{A_{LL}}{D_{LL}}& (8\prime )\end{array}$

SS is more profitable than LL for ∀T > 0 and ∀s > 0, when and only when the A/D ratio is higher for SS than for LL. The area of A/D ratios that satisfy (8′) is illustrated in dark brown in Figure 3 left. Note that this area is identical to the area where A/D ratio of SS is higher than that of LL. The time required for consumption is thus disregarded for comparing the profitability between SS and LL. The finder's share (T) is also disregarded.

FIGURE 3

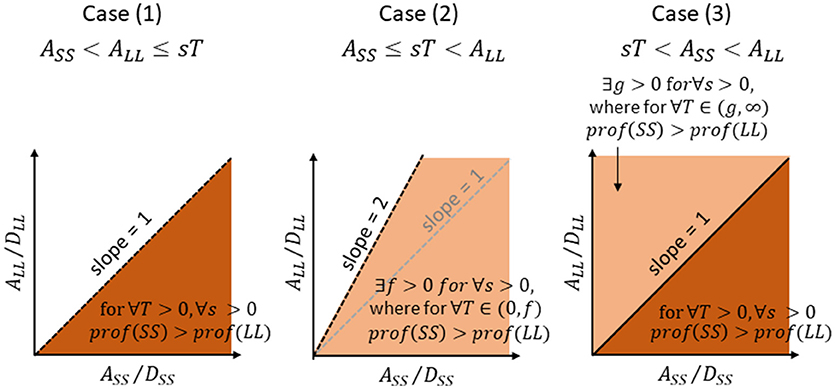
Figure 3. Areas of parameters (amount-to-delay ratio, A/D ratio) for SS (abscissa) and LL (ordinate) where SS gives rise to a higher profitability than LL, for Case (1), Case (2), and Case (3), respectively. See text for further explanations.

Case (2)

Similarly based on (2) and (3), (4) is given as;

$\begin{array}{ll}\frac{A_{SS}}{D_{SS}+A_{SS}/s}>\frac{A_{LL}+sT}{{2D}_{LL}+T+A_{LL}/s}& (9)\end{array}$

which is equivalent with;

$\begin{array}{ll}f=\frac{2A_{SS}(D_{LL}/D_{SS})-A_{LL}}{s}>T& (9\prime )\end{array}$

Considering (5), we have;

$\begin{array}{ll}{A}_{SS}/s\le T<\text{min}\left\{A_{LL}/s,f\right\}& (10)\end{array}$

The upper limit of T exists for ∀s > 0 if the numerator of (9′) is positive, namely when

$\begin{array}{ll}\frac{2A_{SS}}{D_{SS}}>\frac{A_{LL}}{D_{LL}}& (11)\end{array}$

holds. The area of A/D ratios that satisfy (11) is illustrated in light brown in Figure 3 center. Note that this area is wider than the area where A/D ratio of SS is higher than that of LL. If otherwise and f is negative, (9) does not hold for ∀T ≥ 0.

Case (3)

Based on (3), (7) is given as;

$\begin{array}{ll}\frac{A_{SS}+sT}{{2D}_{SS}+T+A_{SS}/s}>\frac{A_{LL}+sT}{{2D}_{LL}+T+A_{LL}/s}& (12)\end{array}$

which is equivalent with;

$\begin{array}{ll}g=\frac{A_{LL}{D}_{SS}-A_{SS}{D}_{LL}}{(D_{LL}-D_{SS})s}<T& (12\prime )\end{array}$

Considering (6), we have;

$\begin{array}{ll}\text{max}\left\{g,0\right\}<T<A_{SS}/s& (13)\end{array}$

When the numerator of (12′) is 0 or negative, g is also negative, so that (12) holds for ∀T ≥ 0. Namely when;

$\begin{array}{ll}\frac{A_{SS}}{D_{SS}}\ge \frac{A_{LL}}{D_{LL}}& (14)\end{array}$

The A/D area that satisfy (14) is illustrated in dark brown in Figure 3 right. If otherwise, the T has a non-zero lower limit given by (12′).

Predictions of the Analytical Model

From the analytical model, we obtain the following lines of prediction.

• P always gains more than S does.

• If not scrounged, the profitability that P gains from SS and LL options follows the respective amount-to-delay ratio (A/D ratio).

• If scrounged and the finder's share (T) is short, profitability of SS can be a higher than that of LL, even when A/D ratio of SS is lower than that of LL.

• For this reversal to occur, the finder's share (T) must be either shorter than an upper limit, or longer than a lower limit, depending on the A/D ratios of SS and LL, and the speed of food consumption (s).

To gain a higher profitability for a given d, S must reduce δ and/or increase v by forming a dense flock of rapidly running foragers. On the other hand, P also has to increase v to counteract S's scrounging. Interactions between S and P would result in an arms race, so v increases to its upper limit given by physiological constraints, and T consequently becomes shorter. The shorter the T, the lower the prof_p would be. However, because SS is more resistant against scrounging than LL, P would choose SS more frequently than LL.

The food supply rate (s) needs a careful consideration. The present analytical model assumes that food is available at once as soon as foragers arrive at F, and the consumption rate is determined by the foragers behavior. Alternatively, the food resource may determine s, a constant that foragers cannot control. We analyzed this alternative situation (Supplementary Text and Figures 1S, 2S) and found basically the same predictions. In either model, a higher s would make P to reduce the scrounging effect and increase prof_p at the same time. The scrounger S also gains by increasing its consumption speed, so that an arms race would arise also for s, leading to its upper limit delineated by physiological constraints.

We may generalize the model to include more than 2 foragers, namely one P and two or more S that scrounge the P's discovery. A group of opportunistic foragers composed of n individuals may encounter food patches at a higher rate than the two foragers assumed here. In this study, however, we focus only on how much does P gain, and we do not consider what S gains. We ignored this because we supposed that only P forms memory associated with food of a certain profitability, whereas S does not update the food memory. This assumption is actually not correct, and chicks in the scrounging situation also learn the association between color cues and the food rewards [30]. Further theoretical and empirical considerations are needed on this point.

A serious consideration must be given for whether the analytical model is realistic. In the following, based on experimental behavioral data we have obtained so far in a series of chick studies, we will construct a numerical simulation further in search of the conditions where SS is more profitable than LL.

Numerical Simulation of Profitability in Social Foraging Situation

We construct numerical simulation to specify the conditions in which the prof_p of SS is higher than that of LL. To do so, we modify some of the assumptions discussed so far. First, we now assume that the amount of food in patch (A) is a discrete value (integer) rather than continuous. Actually, foragers make discrete acts of attack for each piece of food in the patch, rather than smoothly sucking up fluid food. Second, each act of attack adds a certain unitary handling time, reducing prof_p in a stepwise manner. Third, attacks often fail, further reducing prof_p. Finally, and most importantly, the amount (A) varies from a patch to another, even without scrounging. We take these ecologically realistic situations into consideration, together with behavioral parameters obtained in behavioral studies in domestic chicks [30].

Amount and Delay

We assume that the forager sequentially encounters food patches in a field comprising only SS options, or another field comprising only LL options (Figures 4A,B). The forager does not travel, and the time between patch encounters is disregarded. Instead, the forager evaluates each patch by its short-term profitability. In the following, we consider only the profitability gained by the producer (prof_p).

FIGURE 4

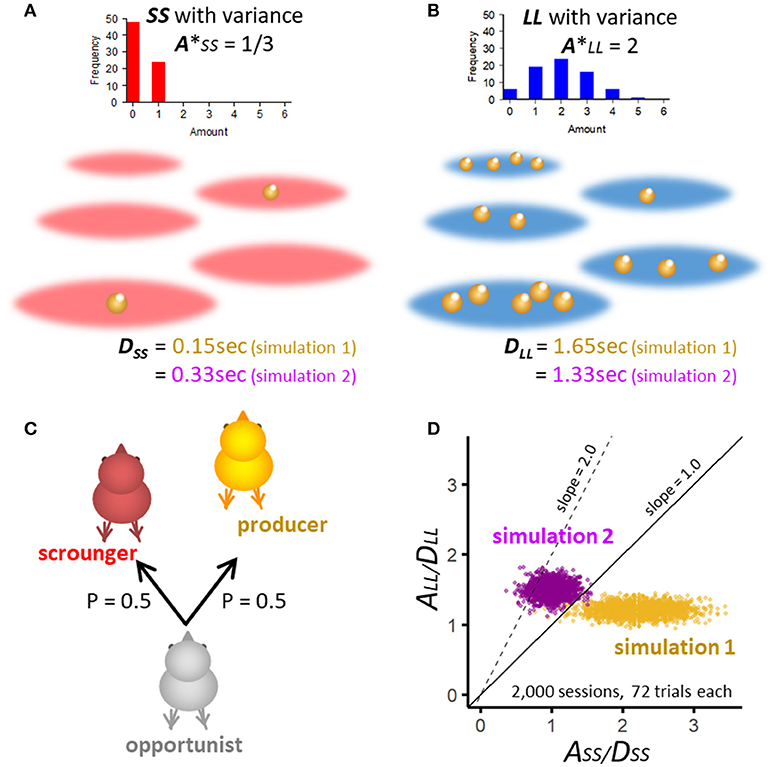
Figure 4. Assumptions of numerical simulation constructed for realistic situations for SS (A) and LL patches (B). For each patch, forager waits for a constant delay time, namely 0.15 s for SS and 1.65 s for LL. To mimic natural food patches, the amount of food items varies randomly according to binomial distribution. The expected amount of food was set as 1/3 for SS and 2 for LL, so that the latter is 6 times larger. (C) Opportunistic forager act producer or scrounger at equal probability = 0.5 in a manner independent from the food amount variations. (D) A/D ratio of randomly generated SS and LL pairs in 2,000 simulated sessions (each composed of 72 trials) are plotted for two sets of simulations. In simulation 1, A/D ratio is distributed mostly in the area where A_SS/D_SS is larger than A_LL/D_LL. In simulation 2, A/D ratio of LL is higher than SS and lies mainly below the line with slope = 2, corresponding to Case (2) of Figure 3.

One patch has a fixed number (A = 1 or 6) of discrete food items, each of which independently becomes available at a probability of 1/3, so that natural variations in food amount in patches are mimicked. In the field comprising SS patches (A = 1, Figure 4A), the expected amount is (A* = 1/3). Similarly, in the field comprising LL patches (A = 6, Figure 4B), the number of food items varies widely with its expected amount 6 times larger than that of SS patches (A* = 2). For these patches, we assume a fixed delay of 0.15 s for SS and 1.65 s for LL. These delay values are taken from our behavioral study [30]. In the numerical simulation we assume;

A: total number of food items in a patch, varies according to binomial distribution; (integer, 0 ≤ A ≤ 6 for LL, 0 ≤ A ≤ 1 for SS).

The simulated opportunistic chick encounters food patches for 72 trials in one session, and the chick acts P or S at equal probability of 0.5 (Figure 4C). Notice that the amount (A) is determined independently of whether the chick acts P or S. Figure 4D shows two sets of simulation, in which A/D ratios of randomly generated SS and LL pairs are plotted in 2,000 sessions, each composed of 72 trials. In simulation 1 (Table 1), delays are chosen so that SS is higher than LL in A*/D ratio. In simulation 2 (Table 2), A*/D ratio of SS is lower than LL but it is distributed mostly below the line of slope = 2.0, corresponding to the parametric area shown in Case (2) of the analytical model (Figure 3).

TABLE 1

Table 1. Amount, delay, and A/D ratio (simulation 1).

TABLE 2

Table 2. Amount, delay, and A/D ratio (simulation 2).

Food Consumption Speed and Profitability Functions

The food consumption speed (s) is a constant determined by the foraging chicks, namely by how quickly and how accurately they attack the food. For one action of attack, the chick invests a unitary handling time (τ). Because attacks (pecks) sometimes fail, the chick repeats attack more times than the number of items, and the ratio (number of attacks per item) is given as κ ≥ 1. The chick also pays an energetic cost for attacks, but it is ignored here. Based on our previous experiments in chicks, we estimate;

τ : handling time per attack: 0.25 (sec/peck)

κ : number of attacks invested per food item: 1.21 (pecks/grain)

Here, τ represents the time invested for one action of pecking, and κ the accuracy of pecking. The food consumption speed (s) is therefore given as;

$\begin{array}{ll}s=1/\tau \kappa =3.31(\text{grain}/\text{sec})& (15)\end{array}$

For $A_{SS}^{*}$ and $A_{LL}^{*}$ shown in Table 1, each of the 3 cases therefore corresponds to the following range of T values;

Case (1): 0.60 ≤ T

Case (2): 0.10 ≤ T < 0.60

Case (3): 0.00 ≤ T < 0.10

In the simulation, following the formula (1), profitability is given for each trial by (2) when;

$\begin{array}{l}A/s=A\tau \kappa \le T\end{array}$

or by (3) when;

$\begin{array}{l}T<A/s=A\tau \kappa \end{array}$

holds, respectively.

Profitability When Scrounging Does Not Occur

Initially, we calculate prof_P for SS and LL under the condition where scrounging does not occur (or T is set 999 sec for ∞) for simulation 1 (Table 3) and 2 (Table 4). Average of prof_P in 2,000 sessions is lower than the prof_P computed for the averaged amount (A*) for both SS and LL. It is because prof_P is given by upward-convex functions in either (2) or (3), so that Jensen's inequality holds. As D_SS is shorter than D_LL, due to a higher degree of non-linearity for SS, a larger difference occurs in SS than in LL.

TABLE 3

Table 3. Profitability (simulation 1).

TABLE 4

Table 4. Profitability (simulation 2).

Profitability When Scrounging Occurs

For simulation 1, we calculated prof_Pin two different conditions, namely when the food amount (A_LL and A_SS) does not vary (Figure 5Aa), and when the amount varies from trial to trial (Figure 5Ab-d), respectively. When the amount does not vary, SS exceeds LL for ∀T ∈ [0, ∞) (Figure 5Aa). When the amount varies, Jensen's inequality occurs, and LL tends to be higher than SS for T = 1.0sec (Figure 5Ac), but not for T = 0.2sec (Figure 5Ab). Further systematic survey for T ∈ [0, 1.0] reveals a reversal at around 0.4–0.6 s (Figure 5Ad); dashed horizontal lines (blue for LL and red for SS) indicate the average of simulated prof_p obtained for T = ∞ or 999. Clearly SS is more resistant against scrounging than LL.

FIGURE 5

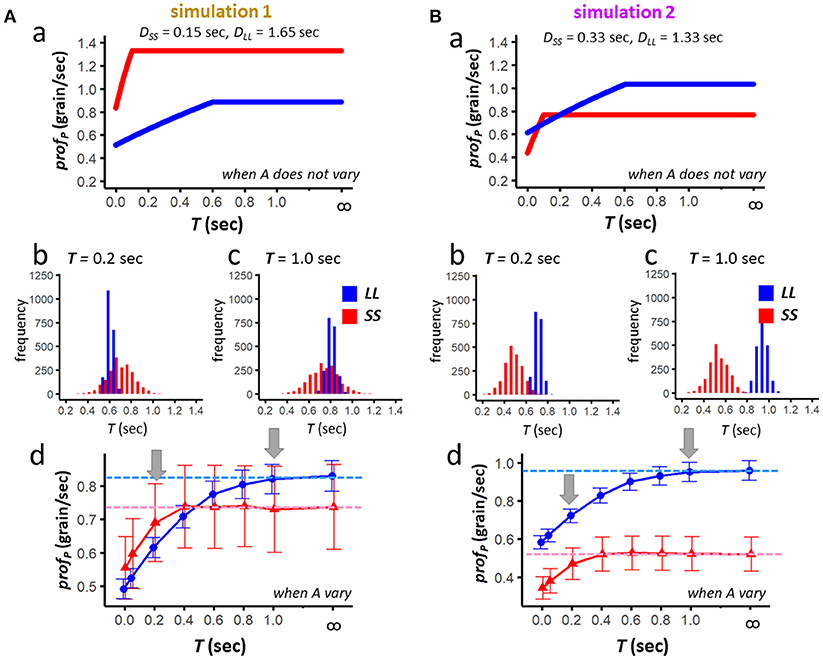
Figure 5. Results of the numerical simulation 1 (A) and simulation 2 (B). For each set of simulation parameters, averaged profitability of LL (blue) and SS (red) is examined in two conditions; namely, when the food amount does not vary (Aa,Ba), and when it varies from trial to trial (Ab–d,Bb–d). Results of 2,000 simulated sessions (each representing average of 72 trials) are shown for T (0.00, 0.05, 0.20, 0.40, 0.60, 0.80, 0.10, and 999 or ∞); mean and standard deviation are shown each. Dashed horizontal lines in (Ad,Bd) denote the profitability when scrounging does not occur.

We also calculated prof_P for simulation 2 in two different conditions (Figure 5B). When the amount does not vary, LL exceeds SS except T = 0.10sec (Ba). When the amount varies, as the effect of the Jensen's inequality is stronger for SS than for LL, LL exceeds SS for ∀T ∈ [0, ∞). Still, as shown in Figure 5Bd, SS is more resistant against scrounging than LL.

Upper and lower limits for T [f and g, given by (9′) and (12′)] are calculated for the averaged amount (A*) of SS and LL such as;

simulation 1:

f = 1.21 (sec), which is higher than 0.6 [the upper limit for Case (2)]

g = −0.038 (sec), which is lower than 0.0 [the lower limit for Case (3)]

simulation 2:

f = 0.295(sec), which is lower than 0.6 [the upper limit for Case (2)]

g = 0.044(sec), which is higher than 0.0 [the lower limit for Case(3)]

In simulation 1, f and g do not need to be considered as limitations, whereas in simulation 2 these values significantly limit the parametric space where SS has a higher profitability than LL.

Following lines of main conclusions are thus drawn;

• Results of the numerical simulations support a prediction of the analytical model that SS can be more profitable than LL when T is short.

• The non-linearity of prof_p functions (upward-convex for amount) makes SS less profitable than LL due to the Jensen's inequality.

• Therefore, if LL has a higher A/D ratio than SS, SS has little chance to exceed LL in profitability under the realistic ecological situation.

Empirical Supports

Perceived Competition for Impulsiveness

When trained in group of three individuals for the conventional ITC task, chicks developed a strongly SS-biased preference (or impulsive choice) by ca. 2-fold compared with those trained alone [30] in good accordance with the theoretical examinations described above. A high level of impulsiveness appeared even when actual conflict of food did not occur. It must also be noticed that the social effects were conditional but not contextual, and the presence of a competitor at the binary choice test did not matter [31], suggesting that the profitability-linked values are stored as lasting reference memory after cumulative experiences of foraging.

However, the amount of food reward should vary at each trial, as those trained with fixed amount (no-risk condition) did not develop impulsive choices [32] in a manner contradictory to what we predict from the profitability variances. Risky food (i.e., larger profitability variance) may generally shift the choice toward indifference, rather than enhanced impulsiveness. The enhanced SS preference in the risk condition is also contradictory to another empirical finding that the chicks are risk averse [33]. When the delay varied, on the other hand, riskier option was given a paradoxically high value [33]. It remains to be intensively studied as to how the risk interacts with the profitability-based decision making.

Social Facilitation of Foraging Effort and Behavioral Synchronization

Patch-use behavior also drastically changes according to social foraging. When a chick was placed in an I-shaped maze equipped with a feeder at each terminal, the chick spontaneously started shuttling between the two feeders. The food (grain of millet) was supplied at variable intervals (1 grain at every 6.7–60 s) without any associated cues. Even in such an uncertain context, chicks allocated the residence time at the two feeders according to the relative gain rate as would be expected by the Herrnstein's matching law in psychology [34] and the ideal free distribution in ecology [35]. When two chicks were placed in the maze (social context), they immediately ran more than in the single context, and the runs were highly synchronized [28, 29]. The social facilitation [36] was accompanied by a precise matching to the reinforcement ratio [37]. See Supplementary Materials for example video clips of the socially-facilitated running and behavioral synchronization. One video (denoted as “single”) shows a pair of chicks separated by opaque wall, so that chicks are invisible to each other. Another video (“pair”) shows those chicks separated by transparent wall. As argued above, foraging pairs try to reduce δ and increase v to their limits, so that the share of the producer (T_p) is minimized. Under such a high scrounging condition, SS could be a better option than LL is in terms of their short-sighted currency of the profitability.

Does the facilitated work-cost really pay? Running more means visiting feeders more frequently, and chicks could personally gain more information about food availability. However, paired chicks may gain public information from their companion. An experimental group of single foragers was confronted with a mirror in the maze, and they also showed socially-facilitated runs, but ended up with under-matching results as in the group of single chicks. Conversely, precise matching was achieved in chicks paired with a real conspecific [37]. These simple experiments gave an answer in favor of the latter public information hypothesis [38, 39]. Collective intelligence could emerge even in such a small group as a pair of chicks.

Embedded Sociality and Ecological Validity

Apparently irrational impulsiveness and excessive work investment could be reasonably accounted for in terms of foraging ecology. In particular, adjustments associated with the producer-scrounger resource conflict proved to be pre-embedded in decisions mechanisms of newly-hatched domestic chicks, allowing them to change decisions flexibly in response to the social and economic circumstances. One is the social impulsivity that is conditionally induced by competition experienced in the past. Another is the social facilitation that appears contextually dependent on the present availability of public information on the food patch from flock companions.

In accord with the social impulsivity, visual perception of a competitor suppressed the neuronal representation of predicted rewards in the basal ganglia [6, 40]. The social facilitation also has neural substrates in the limbic pallium [29, 41]. Lesions to the nucleus accumbens made chicks impulsive [5] just as the competitive training did [30]. Lesions to the limbic pallium caused a perseveration [42] as exemplified by the socially-facilitated foraging [28]. Although the responsible internal processes are yet largely elusive (however, see [43–45] for recent advances in primates and humans), further quantitative analyses of behaviors based on foraging ecology would give us a valid understanding of the hidden processes, leading to the evolutionary basis of learning and cognition [46].

Author Contributions

TM conceived the ideas. YO and HA constructed numeric simulation. YO, HA, and TM wrote the manuscript.

Funding

This study was supported by Grants-in-Aid for Scientific Research from the Japan Society for the Promotion of Science (TM #25291071 and #26650114). YO was funded by JSPS (Grant-in-Aid for JSPS Research Fellow, #26 8054).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling Editor declared a shared affiliation, though no other collaboration, with one of the authors TM.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2018.00049/full#supplementary-material

Videos S1 and S2. Example video clips showing chicks shuttling between two feeders placed at both terminal ends of an I-shaped maze. Food (grains of millet) was delivered a low rate following variable interval schedule. The time of food delivery is indicated by flashing LEDs placed near the feeders. In one video (“Video S1”), chicks were separated by an opaque wall that separated two lanes. In another video (“Video S2”), separation was made by a transparent wall, so that chicks were visible with each other. In both cases, actual conflict of food did not occur, and the competition was fictitious. Distracting motor sounds were added to avoid possible association between the feeders' sound and the delivery of food.

Datasheet 1. Supplementary analysis of an alternative model. This model is constructed with an assumption that the food patch F supplies food at a constant supply rate denoted by s (grain/sec). Basically, the same conclusions are obtained as in the model shown in the main text.

References

1. Stephens DW, Krebs JR. Foraging Theory. Princeton, NJ: Princeton University Press (1986).

Google Scholar

2. Holling CS. Some characteristics of simple types of predation and parasitism. Can Entomol. (1959) 91:385–98. doi: 10.4039/Ent91385-7

CrossRef Full Text | Google Scholar

3. Charnov EL. Optimal foraging: attack strategy of a mantid. Amer Natural. (1976) 110:141–51. doi: 10.1086/283054

CrossRef Full Text | Google Scholar

4. Ainslie GW. Impulse control in pigeons. J Exp Anal Behav. (1974) 21:485–9. doi: 10.1901/jeab.1974.21-485

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Izawa E-I, Zachar G, Yanagihara S, Matsushima T. Localized lesion of caudal part of lobus parolfactorius caused impulsive choice in the domestic chick: evolutionarily conserved function of ventral striatum. J Neurosci. (2003) 23:1894–902. doi: 10.1523/JNEUROSCI.23-05-01894.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Izawa E-I, Aoki N, Matsushima T. Neural correlates of the proximity and quantity of anticipated food rewards in the ventral striatum. Eur J Neurosci. (2005) 22:1502–12. doi: 10.1111/j.1460-9568.2005.04311.x

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Aoki N, Suzuki R, Izawa E-I, Csillag A, Matsushima T. Localized lesions of the ventral striatum, but not the arcopallium, enhanced impulsiveness in the choice based on anticipated spatial proximity of food rewards. Behav Brain Res. (2006) 168:1–12. doi: 10.1016/j.bbr.2005.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Matsushima T, Kawamori A, Bem-Sojka T. Neuro-economics in chicks: foraging choices based on delay, cost and risk. Brain Res Bull. (2008) 76:245–52. doi: 10.1016/j.brainresbull.2008.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Catania KC, Remple FE. Asymptotic prey profitability drives star-nosed moles to the foraging speed limit. Nature (2005) 433:519–22. doi: 10.1038/nature03250

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Charnov EL. Optimal foraging, the marginal value theorem. Theor Popul Biol. (1976) 9:129–36. doi: 10.1016/0040-5809(76)90040-X

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Stephens DW, Anderson D. The adaptive value of preference for immediacy: when shortsighted rules have farsighted consequences. Behav Ecol. (2001) 12:330–9. doi: 10.1093/beheco/12.3.330

CrossRef Full Text | Google Scholar

12. Ishii T, Sakagami T. Self-control and impulsiveness with asynchronous presentation of reinforcement schedules. Behav Proc. (2002) 59:25–35. doi: 10.1016/S0376-6357(02)00059-1

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Stephens DW, Kerr B, Fernández-Juricic E. Impulsiveness without discounting: the ecological rationality hypothesis. Proc R Soc Lond B (2004) 271:2459–65. doi: 10.1098/rspb.2004.2871

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Stevens JR, Stephens DW. The adaptive nature of impulsivity. In: eds Madden GJ, Bickel WK, editors. Impulsivity: The Behavioral and Neurological Science of Discounting. Washington DC: American Psychological Association (2010) p. 361–88.

Google Scholar

15. Hayden BY, Pearson JM, Platt ML. Neuronal basis of sequential foraging decisions in a patchy environment. Nat Neurosci. (2011) 14:933–9. doi: 10.1038/nn.2856

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Blanchard TC, Hayden BY. Monkeys are more patient in a foraging task than in a standard intertemporal choice task. PLoS ONE 10: e0117057. doi: 10.1371/journal.pone.0117057

PubMed Abstract | CrossRef Full Text

17. Hayden BY. Time discounting and time preference in animals a critical review. Psychon Bull Rev. (2016) 23:39–53. doi: 10.3758/s13423-015-0879-3

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hayden BY. Economic choice: the foraging perspective. Curr Opin Behav Sci. (2018) 24:1–6. doi: 10.1016/j.cobeha.2017.12.002

CrossRef Full Text | Google Scholar

19. Matsunami S, Ogura Y, Amita H, Izumi T, Yoshioka M, Matsushima T. Behavioural and pharmacological effects of fluvoxamine on decision-making in food patches and the inter-temporal choices of domestic chicks. Behav Brain Res. (2012) 233:577–86. doi: 10.1016/j.bbr.2012.05.045

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Pearson JM, Hayden BY, Platt ML. Explicit information reduces discounting behavior in monkeys. Front Psychol. (2010) 1:237. doi: 10.3389/fpsyg.2010.00237

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Stevens JR, Hallinan EV, Hauser MD. The ecology and evolution of patience in two new world monkeys. Biol Lett. (2005) 1:223–6. doi: 10.1098/rsbl.2004.0285

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Stevens JR, Rosati AG, Ross KR, Hauser MD. Will travel for food: spatial discounting in two new world monkeys. Curr Biol. (2005) 15:1855–60. doi: 10.1016/j.cub.2005.09.016

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Lewis S, Sherratt TN, Hamer KC, Wanless S. Evidence of intra-specific competition for food in a pelagic seabird. Nature (2001) 412:816–9. doi: 10.1038/35090566

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Giraldeau L-A, Caraco T. Social Foraging Theory. Princeton, NJ: Princeton University Press (2000).

Google Scholar

25. Di Bitetti MS, Janson CH. Social foraging and the finder's share in capuchin monkeys, Cebus apella. Anim Behav. (2001) 62:47–56. doi: 10.1006/anbe.2000.1730

CrossRef Full Text | Google Scholar

26. Morand-Ferron J, Giraldeau L-A, Lefebvre L. Wild carib grackles play a producer-scrounger game. Behav Ecol. (2007) 18:916–21. doi: 10.1093/beheco/arm058

CrossRef Full Text | Google Scholar

27. Arbilly M, Motro U, Feldman MW, Lotem A. Co-evolution of learning complexity and social foraging strategies. J Theor Biol. (2010) 267:573–81. doi: 10.1016/j.jtbi.2010.09.026

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ogura Y, Matsushima T. Social facilitation revisited: increase in foraging efforts and synchronization of running in domestic chicks. Front Neurosci. (2011) 5:91. doi: 10.3389/fnins.2011.00091

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Xin Q, Ogura Y, Uno L, Matsushima T. Selective contribution of the telencephalic arcopallium to the social facilitation of foraging efforts in the domestic chicks. Eur J Neurosci. (2017) 45:365–80. doi: 10.1111/ejn.13475

CrossRef Full Text | Google Scholar

30. Amita H, Kawamori A, Matsushima T. Social influences of competition on impulsive choices in domestic chicks. Biol Lett. (2010) 6:183–6. doi: 10.1098/rsbl.2009.0748

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Amita H., Matsushima T. Instantaneous and cumulative influences of competition on impulsive choices in domestic chicks. Front Neurosci. (2011) 5:101. doi: 10.3389/fnins.2011.00101

CrossRef Full Text

32. Mizuyama R, Uno L, Matsushima T. Food variance and temporal discounting in socially foraging chicks. Anim Behav. (2016) 120:143–51. doi: 10.1016/j.anbehav.2016.07.032

CrossRef Full Text | Google Scholar

33. Kawamori A, Matsushima T. Subjective value of risky foods for individual domestic chicks: a hierarchical Bayesian model. Anim Cogn. (2010) 13:431–41. doi: 10.1007/s10071-009-0293-1

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Herrnstein RJ. The Matching Law. Cambridge, MA: Harvard University Press (1997).

PubMed Abstract | Google Scholar

35. Fretwell ST, Lucas HL. On territorial behavior and other factors influencing habitat distribution in birds, I. Theoretical development. Acta Biotheor. (1969) 19:16–36. doi: 10.1007/BF01601953

CrossRef Full Text | Google Scholar

36. Zajonc RB. Social facilitation. Science (1965) 149:269–74.

PubMed Abstract | Google Scholar

37. Xin Q, Ogura Y, Matsushima T. Four eyes match better than two: Sharing of precise patch-use time among socially foraging domestic chicks. Behav Proc. (2017) 140:127–32. doi: 10.1016/j.beproc.2017.04.020

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Valone TJ. Group foraging, public information, and patch estimation. Oikos (1989) 56:357–63. doi: 10.2307/3565621

CrossRef Full Text | Google Scholar

39. Danchin É, Giraldeau L-A, Valone TJ, Wagner RH. Public information; from nosy neighbors to cultural evolution. Science (2004) 305:487–91. doi: 10.1126/science.1098254

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wen C, Ogura Y, Matsushima T. Striatal and tegmental neurons code critical signals for temporal-difference learning of state value in domestic chicks. Front Neurosci. (2016) 10:476. doi: 10.3389/fnins.2016.00476

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Ogura Y, Izumi T, Yoshioka M, Matsushima T. Dissociation of the neural substrates of foraging effort and its social facilitation in the domestic chick. Behav Brain Res. (2015) 294:162–76. doi: 10.1016/j.bbr.2015.07.052

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Aoki N, Csillag A, Matsushima T. Localized lesion of arcopallium intermedium of the lateral forebrain affected the choice of costly food reward without impairing reward-amount discrimination in the domestic chick. Eur J Neurosci. (2006) 24:2314–26. doi: 10.1111/j.1460-9568.2006.05090.x

CrossRef Full Text

43. Calhoun A J, Hayden BY. The foraging brain. Curr Opin Behav Sci. (2015) 5:24–31. doi: 10.1016/j.cobeha.2015.07.003

CrossRef Full Text | Google Scholar

44. Azab H. Hayden BY. Correlates of decisional dynamics in the dorsal anterior cingulate cortex. Plos Biol. (2017) 15: e2003091. doi: 10.1371/journal.pbio.2003091

CrossRef Full Text | Google Scholar

45. Barack DL, Chang SWC, Platt M. Posterior cingulate neurons dynamically signal decisions to disengage during foraging. Neuron (2017) 96:339–47. doi: 10.1016/j.neuron.2017.09.048

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Rosati AG. Foraging cognition: reviving the ecological intelligence hypothesis. Trends Cogn Sci. (2017) 21:691–702. doi: 10.1016/j.tics.2017.05.011

PubMed Abstract | CrossRef Full Text | Google Scholar