Introduction: In orthopedics, porous metals are promising candidates to replace damaged bones and worn articulations due to their excellent biomechanical compatibility characterized by an open-cell porosity promoting bone ingrowth and compliant mechanical properties, mimicking those of bones. In this communication, stochastic porous metallic structures (foams) intended for biomedical applications are numerically and experimentally investigated from the morphological and structural prospective.
Materials and Methods: Numerically speaking, a multiscale modeling strategy, implying a combination of micro-, meso- and macroscale models, is adopted in this work (Fig 1). The “macroscale” model is intended to represent the foam as a material with equivalent mechanical properties but without porosity (entirely dense). Such properties are determined with the “mesoscale” model where the real foam morphology is taken into account using the representative volume element (RVE) approach. Development of the mesoscale model represents the main objective of this work. An in-house algorithm is used to create randomly-structured open-cell RVEs of different porosity[4]. Each element of the RVE is driven by the “microscale” model where the constitutive relations of the bulk material are considered. In this work, the finite element method and the stereological approach are respectively applied to assess the mechanical properties and the morphology (pore size, shape and distribution) of the numerically-generated foams. Furthermore, in order to have numerical results independent of the stochastic foam structure, the minimum size of an RVE (SRVE,MIN) is determined for different porosities from both the morphological and structural points of view.
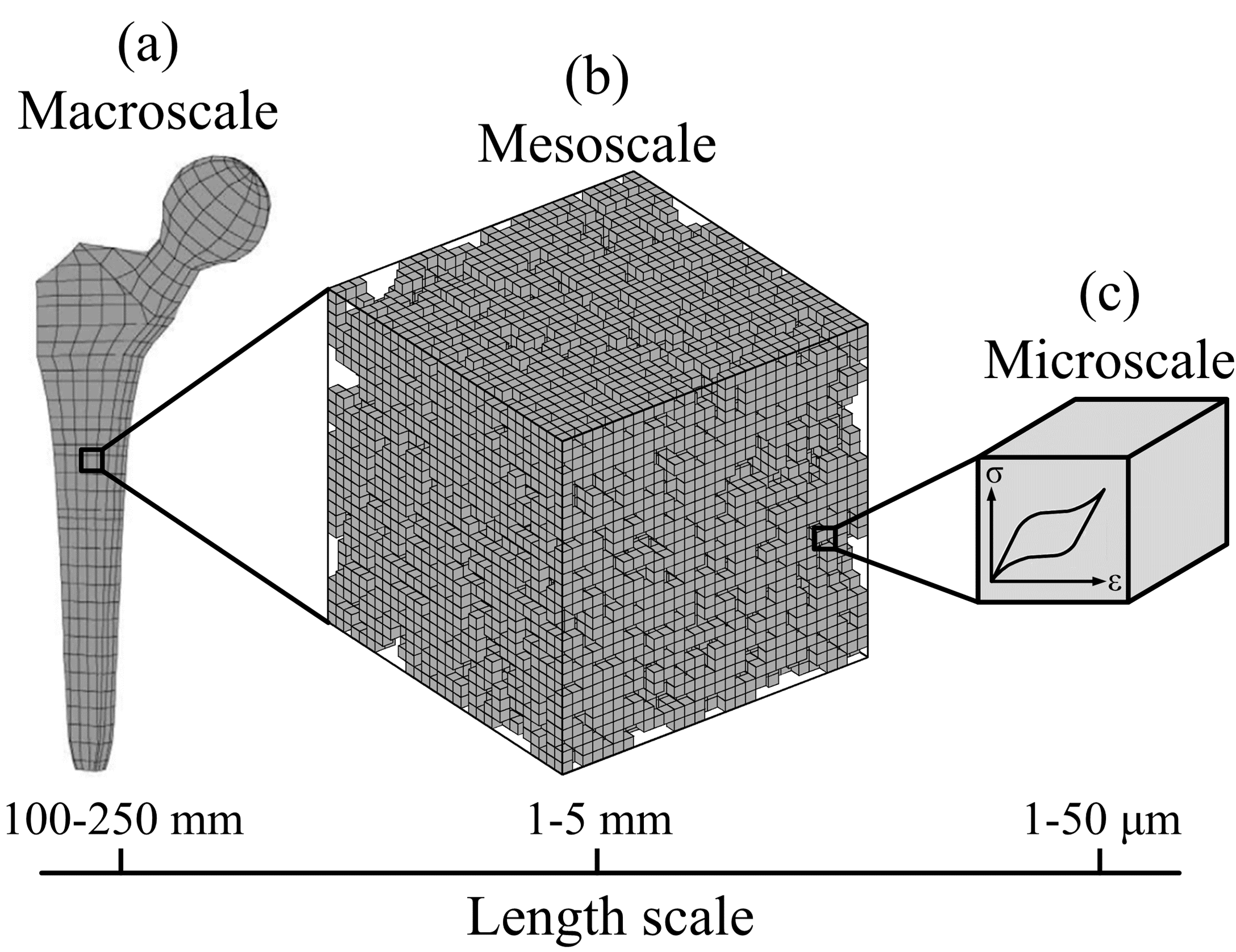
Figure 1: Schematization of the multiscale modeling approach adapted from[4]
Results and Discussion: To experimentally validate the mesoscale model, selective laser melting (SLM), a power bed fusion additive manufacturing process, and cobalt-chrome powder are utilized to produce dumbbell-shaped porosity-gradient tensile specimens designed using the originally-developed stochastic algorithm. A mechanical testing machine coupled with an optical strain measurement system are finally employed to collect the apparent stress-strain diagrams.
Fig 2 presents, as a function of porosity, numerical (solid line) and experimental (dot marks) values of the pore size equivalent diameter (d50) (Fig 2a)[4] and Young’s modulus (E) (Fig 2b)[3]. The evolutions of the minimum RVE size (SRVE,MIN) corresponding to the pore diameter (Fig 2a) and Young’s modulus (Fig 2b) convergence are also plotted. It can be observed that both the morphological (d50) and structural (E) metrics correlate with the experiment, and that larger RVEs are required to reliably represent the foam morphology than their stiffness. Furthermore, since the stiffness of human bone ranges from 5 to 30 GPa[1] and the optimum pore size for bone ingrowth ranges between 50 and 800 µm[2], cobalt-chromium foam with 50% porosity appear to match such requirements, and can therefore be considered for the targeted application.

Figure 2: (a) Pore equivalent diameter (d50) and corresponding minimum RVE (SRVE,min_d50), and (b) Young’s modulus (E) and corresponding SRVE,min_E as functions of porosity.
Conclusion: In this work, we developed and experimentally validated a numerical tool suitable for the prediction of the morphological and mechanical properties of stochastic porous metallic structures. Such a tool is essential for the design of porous implants. Future works will be devoted to the completion of the numerical study to assess the foam mechanical properties beyond the elastic limit and to validate the multiscale modeling approach by producing and testing a porous femoral stem.
The authors would like to credit the Fonds de développement de l'ÉTS (FDETS), Fonds de recherche du Québec – Nature et Technologies (FRQ-NT) and the Natural Sciences and Engineering Research Council of Canada (NSERC) for their financial support.; Computations were conducted on the Guillimin supercomputer from McGill University, managed by Calcul Québec and Compute Canada. The operation of this supercomputer is funded by the Canada Foundation for Innovation (CFI), NanoQuébec, RMGA and the Fonds de recherche du Québec – Nature et Technologies (FRQ-NT).
References:
[1] Currey, J.D., 2012. The structure and mechanics of bone. J. Mater. Sci. 47, 41-54.
[2] Lefebvre, L.-P., 2013. Porous Metals and Metallic Foams in Orthopedic Applications, in: Dukhan, N. (Ed.), Metal Foams: Fundamentals and Applications. DEStech Publications, Inc, Lancaster, pp. 317-362.
[3] Simoneau, C., Brailovski, V., Terriault, P., 2015. Design, manufacture and tensile properties of stochastic porous metallic structures, Submitted to Mech. Mater.
[4] Simoneau, C., Terriault, P., Rivard, J., Brailovski, V., 2014. Modeling of metallic foam morphology using the Representative Volume Element approach: Development and experimental validation. Int. J. Solids Struct. 51, 3633-3641.